2.2.2直线的两点式方程与2.2.3直线一般式方程课件(共23张PPT)
文档属性
| 名称 | 2.2.2直线的两点式方程与2.2.3直线一般式方程课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-24 11:24:38 | ||
图片预览








文档简介
(共23张PPT)
第二章
2.2.2直线的两点式方程
直线的两点式方程
学习目标
1.掌握直线方程两点式的形式、特点及适用范围.
2.了解直线方程截距式的形式、特点及适用范围.
3.会用中点坐标公式求线段的中点坐标.
新课程标准
1.掌握直线的两点式方程和截距式方程.(数学抽象)
2.会选择适当的方程形式求直线方程.(数学抽象)
3.能用直线的两点式方程与截距式方程解答有关问题.(数学运算)
学习重难点
重点:直线方程两点式.
难点:求解直线方程.
复习回顾
直线方程名称 已知 条件
直线方程
使用范围
点斜式
斜截式
点P0(x0,y0)和斜率k
斜率k和直线在y轴上的截距为b
y-y0=k(x-x0)
y = k x +b
斜率必须存在
直线方程的形式
斜率不存在时,直线方程x=x0
直线的斜截式方程
思考
已知直线l经过两点,(其中,),因为两点确定一条直线,所以直线l是唯一确定的.也就是说,对于直线l上的任意一点,它的坐标与点,的坐标之间具有唯一确定的关系,这一关系是什么呢?
由经过两点,的直线的斜率公式可以求出直线l的斜率,因此我们可以利用直线的点斜式方程来解决问题.
当时,经过两点,的直线的斜率. 任取,中的一点,例如,取点,由直线的点斜式方程,得,
当时,上式可写为.
就是经过两点,(其中,)的直线的方程,我们把它叫做直线的两点式方程,简称两点式.
直线的斜截式方程
注意
1
如果或,则直线没有两点式方程.
注意
2
当时,直线垂直于轴,直线方程为,即;
注意
3
当时,直线垂直于y轴,直线方程为,即.
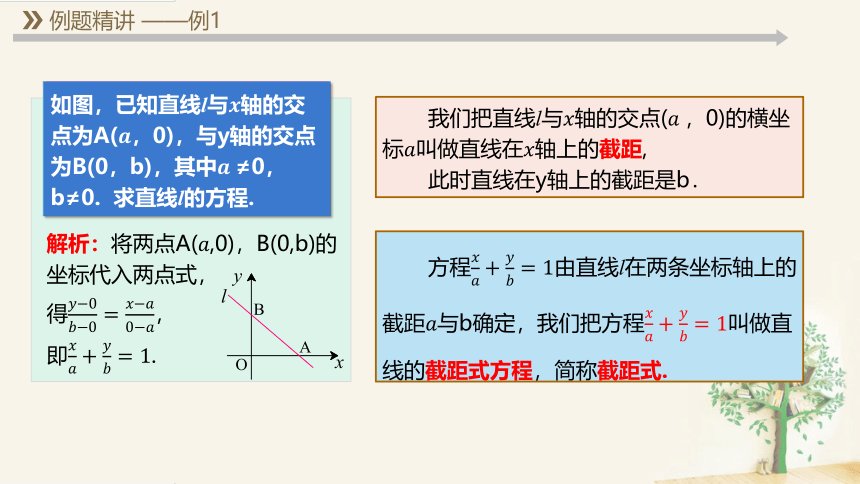
例题精讲 ——例1
我们把直线l与轴的交点(,0)的横坐标叫做直线在轴上的截距,
此时直线在y轴上的截距是b.
方程由直线l在两条坐标轴上的截距与b确定,我们把方程叫做直线的截距式方程,简称截距式.
解析:将两点A(,0),B(0,b)的坐标代入两点式,
得,
即.
如图,已知直线l与轴的交点为A(,0),与y轴的交点为B(0,b),其中≠0,b≠0. 求直线l的方程.
例题精讲 ——例2
已知△ABC的三个顶点A(,0),B(3, 3),C(0,2),求边BC所在直线的方程,以及这条边上的中线 AM所在直线的方程.
例题精讲 ——例2
已知△ABC的三个顶点A(,0),B(3, 3),C(0,2),求边BC所在直线的方程,以及这条边上的中线 AM所在直线的方程.
解:如图,过B(3,3),C(0,2)的两点式方程为,
整理得.这就是边BC所在直线的方程.
边BC上的中线是顶点A与边BC中点M所连线段,由中点坐标公式,可得点M的坐标为,即.
过A(5,0),M两点的直线方程为,
整理可得x+13y+5=0.这就是边 BC上中线AM所在直线的方程.
课堂检测
1.求经过下列两点的直线的两点式方程:
(1) (2,1),; (2) A(0,5),B(5,0).
课堂检测
2.根据下列条件求直线的截距式方程,并画出图形:
(1)在轴、y轴上的截距分别是2,3;
(2)在轴、y轴上的截距分别是5,6.
课堂检测
3.根据下列条件,求直线的方程:
(1)过点(0,5),且在两坐标轴上的截距之和为2;
(2)过点(5,0),且在两坐标轴上的截距之差为2.
第二章
2.2.3直线的一般式方程
直线的一般式方程
任意一条直线l,在其上任取一点(,),当直线l的斜率为k时(此时直线的倾斜角α≠90°),其直线的方程为,这是关于,的二元一次方程.
当直线l的斜率不存在,即直线l的倾斜角α=90°时,直线的方程为.
上述方程可以认为是关于,的二元一次方程,因为此时方程中的系数为0.
方程和都是二元一次方程,因此平面直角坐标系中的任意一条直线都可以用一个关于,的二元一次方程表示.
(1)平面直角坐标系中的任意一条直线都可以用一个关于,的二元一次方程表示吗
思考
分类讨论时,常按和分类,这样可以做到不重不漏.
直线的一般式方程
对于任意一个二元一次方程,(A,B不同时为0),如果能把它化为直线方程的某种形式,那么我们就可以断定它表示一条直线.
当B≠0时,方程可变形为,它表示过点,斜率为的直线.
当B=0时,A≠0,方程可变形为,它表示过点(,0),且垂直于轴的直线.
由上可知,关于,的二元一次方程都表示一条直线.
(2)任意一个关于,的二元一次方程都表示一条直线吗
思考
直线的一般式方程
对于任意一个二元一次方程,(A,B不同时为0),如果能把它化为直线方程的某种形式,那么我们就可以断定它表示一条直线.
当B≠0时,方程可变形为,它表示过点,斜率为的直线.
当B=0时,A≠0,方程可变形为,它表示过点(,0),且垂直于轴的直线.
由上可知,关于,的二元一次方程都表示一条直线.
我们把关于,的二元一次方程(其中A,B不同时为0)叫做直线的一般式方程,简称一般式.
直线的一般式方程
探究
在方程 中,A,B,C为何值时,方程表示的直线: ①平行于轴?平行于轴? 与轴重合?④与轴重合?
①平行于轴的直线,纵坐标不变,横坐标取全体实数,所以B≠0,A=0,C≠0;
②当A≠0,B=0,C≠0时,直线平行于轴;
③当B≠0,A=0,C=0时,与轴重合.
④当A≠0,B=0,C=0时,与轴重合.
例题精讲 ——例1
已知直线经过点A(6,4),斜率为,求直线的点斜式和一般式方程.
解:经过点A(6, 4),斜率为的直线的点斜式方程是:
,
化为一般式,得.
例题精讲 ——例2
把直线l的一般式方程化为斜截式,求出直线l的斜率以及它在轴与轴上的截距,并画出图形.
分析:求直线l在轴上的截距,即求直线l与轴交点的横坐标,只要在直线l的方程中令=0即可得的值.
例题精讲 ——例2
把直线l的一般式方程化为斜截式,求出直线l的斜率以及它在轴与轴上的截距,并画出图形.
解:把直线l的一般式方程化为斜截式.
因此,直线l的斜率k,它在y轴上的截距是3.
在直线l的方程中,令y=0,得,
即直线l在轴上的截距是.
由上面可得直线l与轴、y轴的交点分别为A (,0),B(0,3),
过A,B两点作直线,就得直线l.
在直角坐标系中画直线时,通常找出直线与两条坐标轴的交点,然后连接这两个点.
课堂检测
1.根据下列条件,写出直线的方程,并把它化为一般式:
(1)经过点A(8,2),斜率是,
(2)经过点B(4,2)平行于轴;
(3)经过点,;
(4)在轴、 轴的截距分别是,3.
课堂检测
2.求下列直线的斜率以及在y轴上的截距,并画出图形:
(1); (2);
(3)x+2y=0; (4)7x 6y+4=0.
课堂检测
3.已知直线l的方程是Ax+By+C=0.
(1)当B≠0时,直线l的斜率是多少?当B=0时呢?
(2)系数A,B,C取什么值时,方程Ax+By+C=0表示经过原点的直线?
求直线方程时方程形式的选择技巧
(1)已知一点的坐标,求过该点的直线方程时,通常选用点斜式方程.
(2)已知直线的斜率,通常选用点斜式或斜截式,再由其他条件确定一个定点的坐标或在y轴上的截距.
(3)已知直线在两坐标轴上的截距时,通常选用截距式方程.
(4)已知直线上两点时,通常选用两点式方程.
课堂小结
第二章
2.2.2直线的两点式方程
直线的两点式方程
学习目标
1.掌握直线方程两点式的形式、特点及适用范围.
2.了解直线方程截距式的形式、特点及适用范围.
3.会用中点坐标公式求线段的中点坐标.
新课程标准
1.掌握直线的两点式方程和截距式方程.(数学抽象)
2.会选择适当的方程形式求直线方程.(数学抽象)
3.能用直线的两点式方程与截距式方程解答有关问题.(数学运算)
学习重难点
重点:直线方程两点式.
难点:求解直线方程.
复习回顾
直线方程名称 已知 条件
直线方程
使用范围
点斜式
斜截式
点P0(x0,y0)和斜率k
斜率k和直线在y轴上的截距为b
y-y0=k(x-x0)
y = k x +b
斜率必须存在
直线方程的形式
斜率不存在时,直线方程x=x0
直线的斜截式方程
思考
已知直线l经过两点,(其中,),因为两点确定一条直线,所以直线l是唯一确定的.也就是说,对于直线l上的任意一点,它的坐标与点,的坐标之间具有唯一确定的关系,这一关系是什么呢?
由经过两点,的直线的斜率公式可以求出直线l的斜率,因此我们可以利用直线的点斜式方程来解决问题.
当时,经过两点,的直线的斜率. 任取,中的一点,例如,取点,由直线的点斜式方程,得,
当时,上式可写为.
就是经过两点,(其中,)的直线的方程,我们把它叫做直线的两点式方程,简称两点式.
直线的斜截式方程
注意
1
如果或,则直线没有两点式方程.
注意
2
当时,直线垂直于轴,直线方程为,即;
注意
3
当时,直线垂直于y轴,直线方程为,即.
例题精讲 ——例1
我们把直线l与轴的交点(,0)的横坐标叫做直线在轴上的截距,
此时直线在y轴上的截距是b.
方程由直线l在两条坐标轴上的截距与b确定,我们把方程叫做直线的截距式方程,简称截距式.
解析:将两点A(,0),B(0,b)的坐标代入两点式,
得,
即.
如图,已知直线l与轴的交点为A(,0),与y轴的交点为B(0,b),其中≠0,b≠0. 求直线l的方程.
例题精讲 ——例2
已知△ABC的三个顶点A(,0),B(3, 3),C(0,2),求边BC所在直线的方程,以及这条边上的中线 AM所在直线的方程.
例题精讲 ——例2
已知△ABC的三个顶点A(,0),B(3, 3),C(0,2),求边BC所在直线的方程,以及这条边上的中线 AM所在直线的方程.
解:如图,过B(3,3),C(0,2)的两点式方程为,
整理得.这就是边BC所在直线的方程.
边BC上的中线是顶点A与边BC中点M所连线段,由中点坐标公式,可得点M的坐标为,即.
过A(5,0),M两点的直线方程为,
整理可得x+13y+5=0.这就是边 BC上中线AM所在直线的方程.
课堂检测
1.求经过下列两点的直线的两点式方程:
(1) (2,1),; (2) A(0,5),B(5,0).
课堂检测
2.根据下列条件求直线的截距式方程,并画出图形:
(1)在轴、y轴上的截距分别是2,3;
(2)在轴、y轴上的截距分别是5,6.
课堂检测
3.根据下列条件,求直线的方程:
(1)过点(0,5),且在两坐标轴上的截距之和为2;
(2)过点(5,0),且在两坐标轴上的截距之差为2.
第二章
2.2.3直线的一般式方程
直线的一般式方程
任意一条直线l,在其上任取一点(,),当直线l的斜率为k时(此时直线的倾斜角α≠90°),其直线的方程为,这是关于,的二元一次方程.
当直线l的斜率不存在,即直线l的倾斜角α=90°时,直线的方程为.
上述方程可以认为是关于,的二元一次方程,因为此时方程中的系数为0.
方程和都是二元一次方程,因此平面直角坐标系中的任意一条直线都可以用一个关于,的二元一次方程表示.
(1)平面直角坐标系中的任意一条直线都可以用一个关于,的二元一次方程表示吗
思考
分类讨论时,常按和分类,这样可以做到不重不漏.
直线的一般式方程
对于任意一个二元一次方程,(A,B不同时为0),如果能把它化为直线方程的某种形式,那么我们就可以断定它表示一条直线.
当B≠0时,方程可变形为,它表示过点,斜率为的直线.
当B=0时,A≠0,方程可变形为,它表示过点(,0),且垂直于轴的直线.
由上可知,关于,的二元一次方程都表示一条直线.
(2)任意一个关于,的二元一次方程都表示一条直线吗
思考
直线的一般式方程
对于任意一个二元一次方程,(A,B不同时为0),如果能把它化为直线方程的某种形式,那么我们就可以断定它表示一条直线.
当B≠0时,方程可变形为,它表示过点,斜率为的直线.
当B=0时,A≠0,方程可变形为,它表示过点(,0),且垂直于轴的直线.
由上可知,关于,的二元一次方程都表示一条直线.
我们把关于,的二元一次方程(其中A,B不同时为0)叫做直线的一般式方程,简称一般式.
直线的一般式方程
探究
在方程 中,A,B,C为何值时,方程表示的直线: ①平行于轴?平行于轴? 与轴重合?④与轴重合?
①平行于轴的直线,纵坐标不变,横坐标取全体实数,所以B≠0,A=0,C≠0;
②当A≠0,B=0,C≠0时,直线平行于轴;
③当B≠0,A=0,C=0时,与轴重合.
④当A≠0,B=0,C=0时,与轴重合.
例题精讲 ——例1
已知直线经过点A(6,4),斜率为,求直线的点斜式和一般式方程.
解:经过点A(6, 4),斜率为的直线的点斜式方程是:
,
化为一般式,得.
例题精讲 ——例2
把直线l的一般式方程化为斜截式,求出直线l的斜率以及它在轴与轴上的截距,并画出图形.
分析:求直线l在轴上的截距,即求直线l与轴交点的横坐标,只要在直线l的方程中令=0即可得的值.
例题精讲 ——例2
把直线l的一般式方程化为斜截式,求出直线l的斜率以及它在轴与轴上的截距,并画出图形.
解:把直线l的一般式方程化为斜截式.
因此,直线l的斜率k,它在y轴上的截距是3.
在直线l的方程中,令y=0,得,
即直线l在轴上的截距是.
由上面可得直线l与轴、y轴的交点分别为A (,0),B(0,3),
过A,B两点作直线,就得直线l.
在直角坐标系中画直线时,通常找出直线与两条坐标轴的交点,然后连接这两个点.
课堂检测
1.根据下列条件,写出直线的方程,并把它化为一般式:
(1)经过点A(8,2),斜率是,
(2)经过点B(4,2)平行于轴;
(3)经过点,;
(4)在轴、 轴的截距分别是,3.
课堂检测
2.求下列直线的斜率以及在y轴上的截距,并画出图形:
(1); (2);
(3)x+2y=0; (4)7x 6y+4=0.
课堂检测
3.已知直线l的方程是Ax+By+C=0.
(1)当B≠0时,直线l的斜率是多少?当B=0时呢?
(2)系数A,B,C取什么值时,方程Ax+By+C=0表示经过原点的直线?
求直线方程时方程形式的选择技巧
(1)已知一点的坐标,求过该点的直线方程时,通常选用点斜式方程.
(2)已知直线的斜率,通常选用点斜式或斜截式,再由其他条件确定一个定点的坐标或在y轴上的截距.
(3)已知直线在两坐标轴上的截距时,通常选用截距式方程.
(4)已知直线上两点时,通常选用两点式方程.
课堂小结
