6.2 立方根 课件(共23张PPT)
图片预览







文档简介
(共23张PPT)
人教版 七年级下
6.2 立方根
1. 想一想:
(1) 16的平方根是______;
(2)-16的平方根________;
(3)0的平方根是________.
复旧导新
问题:
平方根是如何定义的
不存在
0
1. 想一想
问题:
要设计一个体积为27 cm3的正方体形状的魔方,这种魔方的棱长应该是多少
引入新课
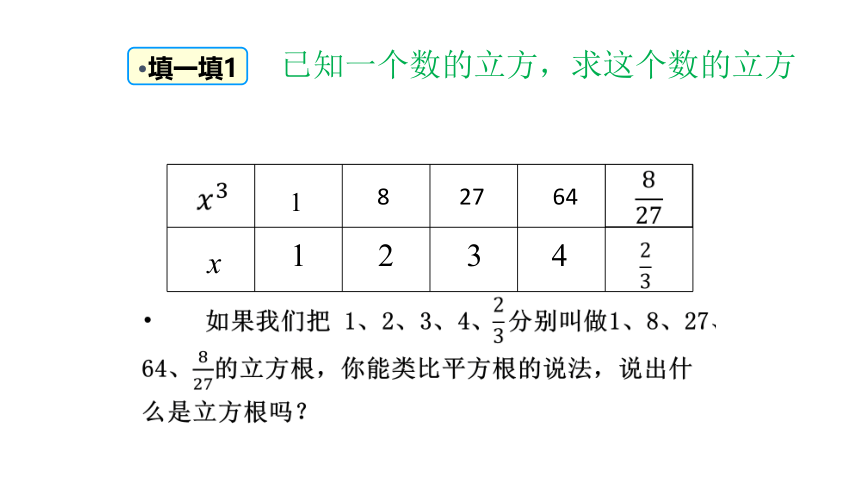
已知一个数的立方,求这个数的问题
8 27 64
填一填1
1
2
3
4
已知一个数的立方,求这个数的立方
3. 试一试
你能给数的立方根下个定义吗?
一般地,如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根.
即:如果x3=a,那么x叫做a的立方根.
求一个数的立方根的运算,叫做开立方.
(1) 因为2 =8,所以8的立方根是( );
(2) 因为( ) =0.125,所以0.125的立方是( );
(3)因为( ) =0,所以0的立方根是( );
(4)因为 ( ) =-8,所以-8的立方根是( );
(5)因为( ) =- -,所以-- 的立方根
是( ).
3
333
3
3
27
27
8
8
活动二 启发诱导,探索新知
2
0.5
0.5
0
0
探究题中正数、0和负数的立方根各有什么特点
1. 探究
33
33
2.说一说
观察练习题中正数、0和负数的立方根各有什么特点
正数的立方根是正数,
负数的立方根是负数,
0的立方根是0.
3. 自主探究
如何表示一个数的立方根
一个数a的立方根可以表示为:
读作:三次根号 a ,
其中a是被开方数,3是根指数,不能省略.
根指数
被开方数
a
3
观察以上算式,想一想:
一个正数有几个立方根,
负数有几个立方根
0呢?
1、正数有一个正的立方根
2、负数有一个负的立方根
3、0的立方根还是0
说明:立方根的个数的性质可以概括为立方根的唯一性,即一个数的立方根是唯一的.
比一比立方根的性质与平方根性质有何不同
立方根的性质:
立方根和平方根的相同与不同?
合作交流
相同:
不同:
零的平方根和立方根都是零。
正数有一正一负两个平方根,而正数只有一个正立方根。
平方根的根指数“2”可以省略,但立方根的根指数“3”绝对不能省。
负数没有平方根,而负数有一个负的立方根。
被开方数的取值范围不同:开平方时被开方数要大于或等于0,而开立方时被开方数可以是任何实数
立方根是它本身的数有哪些
有1, -1, 0
平方根是它本身的数呢
只有0
想一想
算术平方根是它本身的数呢
有1、0
观察下面的运算,请你找出其中的规律
规律是:
①被开方数每扩大 倍,其结果就扩大 倍;
②被开方数每缩小 倍,其结果就缩小 倍.
反之也成立.
1
10
0.1
1000
10
1.1
110
60
0.6
1000
10
开立方的性质
例1 求下列各数的立方根.
(4) 0.064
(5) 0
(6) -8
解:
例2,求下列各式的值:
例3.解下列方程
(1) x3=343
(2)(x-1)3=125
例4 用计算器求下列各数的立方根:343,-1.331.
解:依次按键:
显示:7
所以,
2ndF
4
3
3
=
依次按键:
显示:-1.1
所以,
2ndF
1
(-)
.
3
1
3
=
由于一个数的立方根可能是无限不循环小数,所以我们可以利用计算器求一个数的立方根或它的近似值.
例5 用计算器求 的近似值(精确到0.001).
解 依次按键:
显示:1.259 921 05
所以,
2ndF
=
2
错误
正确
当堂练习
0.5
-3
10
1
1.判断正误.
3.求下列式中x的值.
(1)x3=0.008; (2)(x-1)3=27.
答案:(1)x=0.2;(2)x=4;
课堂小结
立方根
立方根的概念及性质
开立方及相关运算
https://www.21cnjy.com/help/help_extract.php
人教版 七年级下
6.2 立方根
1. 想一想:
(1) 16的平方根是______;
(2)-16的平方根________;
(3)0的平方根是________.
复旧导新
问题:
平方根是如何定义的
不存在
0
1. 想一想
问题:
要设计一个体积为27 cm3的正方体形状的魔方,这种魔方的棱长应该是多少
引入新课
已知一个数的立方,求这个数的问题
8 27 64
填一填1
1
2
3
4
已知一个数的立方,求这个数的立方
3. 试一试
你能给数的立方根下个定义吗?
一般地,如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根.
即:如果x3=a,那么x叫做a的立方根.
求一个数的立方根的运算,叫做开立方.
(1) 因为2 =8,所以8的立方根是( );
(2) 因为( ) =0.125,所以0.125的立方是( );
(3)因为( ) =0,所以0的立方根是( );
(4)因为 ( ) =-8,所以-8的立方根是( );
(5)因为( ) =- -,所以-- 的立方根
是( ).
3
333
3
3
27
27
8
8
活动二 启发诱导,探索新知
2
0.5
0.5
0
0
探究题中正数、0和负数的立方根各有什么特点
1. 探究
33
33
2.说一说
观察练习题中正数、0和负数的立方根各有什么特点
正数的立方根是正数,
负数的立方根是负数,
0的立方根是0.
3. 自主探究
如何表示一个数的立方根
一个数a的立方根可以表示为:
读作:三次根号 a ,
其中a是被开方数,3是根指数,不能省略.
根指数
被开方数
a
3
观察以上算式,想一想:
一个正数有几个立方根,
负数有几个立方根
0呢?
1、正数有一个正的立方根
2、负数有一个负的立方根
3、0的立方根还是0
说明:立方根的个数的性质可以概括为立方根的唯一性,即一个数的立方根是唯一的.
比一比立方根的性质与平方根性质有何不同
立方根的性质:
立方根和平方根的相同与不同?
合作交流
相同:
不同:
零的平方根和立方根都是零。
正数有一正一负两个平方根,而正数只有一个正立方根。
平方根的根指数“2”可以省略,但立方根的根指数“3”绝对不能省。
负数没有平方根,而负数有一个负的立方根。
被开方数的取值范围不同:开平方时被开方数要大于或等于0,而开立方时被开方数可以是任何实数
立方根是它本身的数有哪些
有1, -1, 0
平方根是它本身的数呢
只有0
想一想
算术平方根是它本身的数呢
有1、0
观察下面的运算,请你找出其中的规律
规律是:
①被开方数每扩大 倍,其结果就扩大 倍;
②被开方数每缩小 倍,其结果就缩小 倍.
反之也成立.
1
10
0.1
1000
10
1.1
110
60
0.6
1000
10
开立方的性质
例1 求下列各数的立方根.
(4) 0.064
(5) 0
(6) -8
解:
例2,求下列各式的值:
例3.解下列方程
(1) x3=343
(2)(x-1)3=125
例4 用计算器求下列各数的立方根:343,-1.331.
解:依次按键:
显示:7
所以,
2ndF
4
3
3
=
依次按键:
显示:-1.1
所以,
2ndF
1
(-)
.
3
1
3
=
由于一个数的立方根可能是无限不循环小数,所以我们可以利用计算器求一个数的立方根或它的近似值.
例5 用计算器求 的近似值(精确到0.001).
解 依次按键:
显示:1.259 921 05
所以,
2ndF
=
2
错误
正确
当堂练习
0.5
-3
10
1
1.判断正误.
3.求下列式中x的值.
(1)x3=0.008; (2)(x-1)3=27.
答案:(1)x=0.2;(2)x=4;
课堂小结
立方根
立方根的概念及性质
开立方及相关运算
https://www.21cnjy.com/help/help_extract.php
