北京版六年级下册数学第一单元 圆柱与圆锥 同步练习题(含答案)
文档属性
| 名称 | 北京版六年级下册数学第一单元 圆柱与圆锥 同步练习题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 48.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-24 15:09:49 | ||
图片预览



文档简介
北京版六年级下册数学第一单元 圆柱与圆锥 同步练习题
一.选择题
1.一个圆柱体,高是底面直径的π倍,将它的侧面沿高展开后是( )。
A.长方形 B.正方形 C.平行四边形
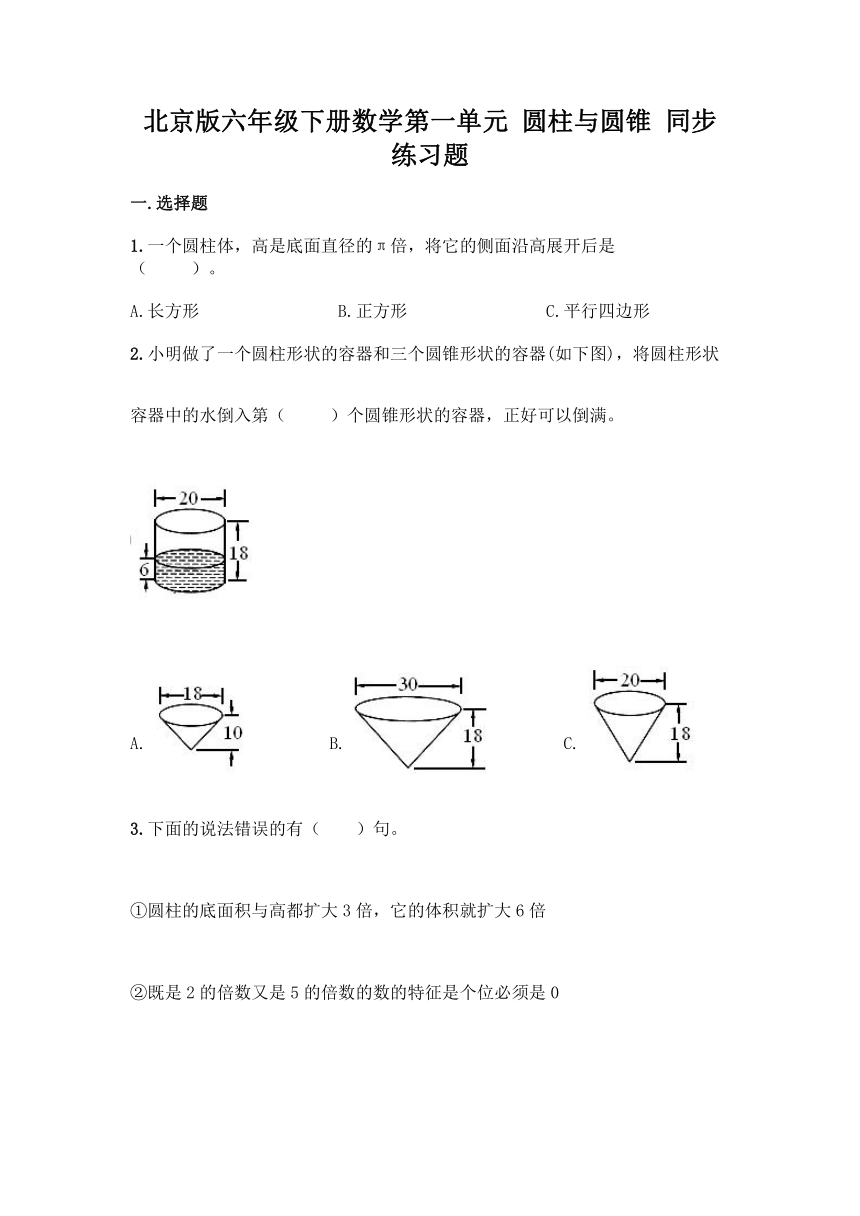
2.小明做了一个圆柱形状的容器和三个圆锥形状的容器(如下图),将圆柱形状容器中的水倒入第( )个圆锥形状的容器,正好可以倒满。
A. B. C.
3.下面的说法错误的有( )句。
①圆柱的底面积与高都扩大3倍,它的体积就扩大6倍
②既是2的倍数又是5的倍数的数的特征是个位必须是0
③一条线段绕着它的一个端点旋转120°,形成的图形是圆
④在长方体上,我们找不到两条既不平行也不相交的线段
⑤公式S梯形 =(a+b)h÷2,当a=b时,就是平行四边形的面积计算公式
A.1 B.2 C.3 D.4
4.一张长方形纸,长6.28分米,宽3.14分米,如果以它为侧面,那么以下( )。的圆形纸片能和它配成圆柱体.
A.直径1厘米 B.半径1分米 C.周长9.42分米 D.面积18.5平方厘米
5.以直角三角形的一条直角边所在的直线为轴,旋转一周,就能得到一个( )。
A.长方体 B.圆锥 C.圆柱 D.正方体
二.判断题
1.圆锥的体积等于圆柱体积的。 ( )
2.只要长方体与圆柱体的底面积相等、高也相等,它们的体积就一定相等。( )
3.圆锥的底面半径扩大到原来的3倍,高不变,体积也扩大到原来的3倍。( )
4.以直角三角形任意一条直角边为轴旋转一周,可以形成一个圆柱。( )
5.一个圆锥体的体积扩大到原来的3倍,它就变成了圆柱体。 ( )
三.填空题
1.圆柱有( )条高,圆锥有( )条高。
2.如图是一个直角三角形,以6cm的直角边所在直线为轴旋转一周,所得到的图形是( ),它的体积是( )cm3。
3.一个圆柱的侧面展开图是一个正方形,高是25.12 cm,这个圆柱的底面半径是( )cm。
4.有五根小棒,分别长1厘米、3厘米、4厘米、5厘米、9厘米,从中选三根小棒围成一个直角三角形,这个直角三角形的面积是( )cm2;如果以其中的一条直角边为轴旋转一周,形成立体图形的体积最小是( )cm3。
5.已知一个圆锥的底面直径是4厘米,高是6厘米,这个圆锥的体积是( )立方厘米。
四.计算题
1.图中圆柱比圆锥的体积大40立方厘米,圆锥的体积是多少立方厘米?
2.求下面圆柱的表面积。
五.解答题
1.一个圆锥形沙堆,底面积是45.9m2, 高1.2m.用这堆沙在12m宽的路面上铺3cm厚的路基,能铺多少米?
2.如图,用彩带捆扎一个圆柱形礼盒,打结处用了35厘米长的彩带,礼盒的底面周长是94.2厘米,高是10厘米,求一共用了多长的彩带?
3.一个圆柱形的粮仓,从里面量得底面直径是3米,装有2.5米高的小麦.如果每立方米小麦重0.7吨,这个粮仓装有多少吨的小麦?
4.展览厅有8根同样的圆柱,柱高10米,直径1米,全都刷上油漆,如果每平方米用油漆100克,需要油漆多少千克?
5.一个圆柱形铁皮水桶(无盖),高10dm,底面直径是6dm,做这个水桶大约要用多少铁皮?
参考答案
一.选择题
1.B
2.C
3.B
4.B
5.B
二.判断题
1.×
2.√
3.×
4.×
5.×
三.填空题
1.无数;1
2.圆锥;25.12
3.4
4.6;37.68
5.25.12
四.计算题
1.40÷2=20立方厘米 答:圆锥的体积是20立方厘米。
2.3.14×()2×2+3.14×9×18=635.85(cm2)
五.解答题
1.3厘米=0.03米
×45.9×1.2÷(12×0.03)
=18.36÷0.36
=51(米)
答:能铺51米。
2.解:94.2÷3.14×8+10×8+35
=240+80+35
=355(厘米)
答:一共用了355厘米的彩带。
3.圆柱形的粮仓的半径:3÷2=1.5(米)
14×1.52×2.5
=3.14×2.25×2.5
=17.6625(立方米)
这个粮仓装有小麦的吨数:0.7×17.6625=12.36375(吨)
答:这个粮仓装有12.36375吨的小麦。
4.8根圆柱的表面积:3.14×1×10×8=251.2(平方米)需要的油漆的重量:251.2×100=25120(克)=25.12(千克)
答:需要油漆25.12千克。
5.3.14×6×10+3.14×(6÷2)2
=18.84×10+3.14×9
=188.4+28.26
=216.66(平方分米)
答:做这个水桶大约要用铁皮216.66平方分米。
一.选择题
1.一个圆柱体,高是底面直径的π倍,将它的侧面沿高展开后是( )。
A.长方形 B.正方形 C.平行四边形
2.小明做了一个圆柱形状的容器和三个圆锥形状的容器(如下图),将圆柱形状容器中的水倒入第( )个圆锥形状的容器,正好可以倒满。
A. B. C.
3.下面的说法错误的有( )句。
①圆柱的底面积与高都扩大3倍,它的体积就扩大6倍
②既是2的倍数又是5的倍数的数的特征是个位必须是0
③一条线段绕着它的一个端点旋转120°,形成的图形是圆
④在长方体上,我们找不到两条既不平行也不相交的线段
⑤公式S梯形 =(a+b)h÷2,当a=b时,就是平行四边形的面积计算公式
A.1 B.2 C.3 D.4
4.一张长方形纸,长6.28分米,宽3.14分米,如果以它为侧面,那么以下( )。的圆形纸片能和它配成圆柱体.
A.直径1厘米 B.半径1分米 C.周长9.42分米 D.面积18.5平方厘米
5.以直角三角形的一条直角边所在的直线为轴,旋转一周,就能得到一个( )。
A.长方体 B.圆锥 C.圆柱 D.正方体
二.判断题
1.圆锥的体积等于圆柱体积的。 ( )
2.只要长方体与圆柱体的底面积相等、高也相等,它们的体积就一定相等。( )
3.圆锥的底面半径扩大到原来的3倍,高不变,体积也扩大到原来的3倍。( )
4.以直角三角形任意一条直角边为轴旋转一周,可以形成一个圆柱。( )
5.一个圆锥体的体积扩大到原来的3倍,它就变成了圆柱体。 ( )
三.填空题
1.圆柱有( )条高,圆锥有( )条高。
2.如图是一个直角三角形,以6cm的直角边所在直线为轴旋转一周,所得到的图形是( ),它的体积是( )cm3。
3.一个圆柱的侧面展开图是一个正方形,高是25.12 cm,这个圆柱的底面半径是( )cm。
4.有五根小棒,分别长1厘米、3厘米、4厘米、5厘米、9厘米,从中选三根小棒围成一个直角三角形,这个直角三角形的面积是( )cm2;如果以其中的一条直角边为轴旋转一周,形成立体图形的体积最小是( )cm3。
5.已知一个圆锥的底面直径是4厘米,高是6厘米,这个圆锥的体积是( )立方厘米。
四.计算题
1.图中圆柱比圆锥的体积大40立方厘米,圆锥的体积是多少立方厘米?
2.求下面圆柱的表面积。
五.解答题
1.一个圆锥形沙堆,底面积是45.9m2, 高1.2m.用这堆沙在12m宽的路面上铺3cm厚的路基,能铺多少米?
2.如图,用彩带捆扎一个圆柱形礼盒,打结处用了35厘米长的彩带,礼盒的底面周长是94.2厘米,高是10厘米,求一共用了多长的彩带?
3.一个圆柱形的粮仓,从里面量得底面直径是3米,装有2.5米高的小麦.如果每立方米小麦重0.7吨,这个粮仓装有多少吨的小麦?
4.展览厅有8根同样的圆柱,柱高10米,直径1米,全都刷上油漆,如果每平方米用油漆100克,需要油漆多少千克?
5.一个圆柱形铁皮水桶(无盖),高10dm,底面直径是6dm,做这个水桶大约要用多少铁皮?
参考答案
一.选择题
1.B
2.C
3.B
4.B
5.B
二.判断题
1.×
2.√
3.×
4.×
5.×
三.填空题
1.无数;1
2.圆锥;25.12
3.4
4.6;37.68
5.25.12
四.计算题
1.40÷2=20立方厘米 答:圆锥的体积是20立方厘米。
2.3.14×()2×2+3.14×9×18=635.85(cm2)
五.解答题
1.3厘米=0.03米
×45.9×1.2÷(12×0.03)
=18.36÷0.36
=51(米)
答:能铺51米。
2.解:94.2÷3.14×8+10×8+35
=240+80+35
=355(厘米)
答:一共用了355厘米的彩带。
3.圆柱形的粮仓的半径:3÷2=1.5(米)
14×1.52×2.5
=3.14×2.25×2.5
=17.6625(立方米)
这个粮仓装有小麦的吨数:0.7×17.6625=12.36375(吨)
答:这个粮仓装有12.36375吨的小麦。
4.8根圆柱的表面积:3.14×1×10×8=251.2(平方米)需要的油漆的重量:251.2×100=25120(克)=25.12(千克)
答:需要油漆25.12千克。
5.3.14×6×10+3.14×(6÷2)2
=18.84×10+3.14×9
=188.4+28.26
=216.66(平方分米)
答:做这个水桶大约要用铁皮216.66平方分米。
