3.4 函数的应用(一) 课件(共23张PPT)
文档属性
| 名称 | 3.4 函数的应用(一) 课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 803.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-25 04:40:37 | ||
图片预览







文档简介
(共23张PPT)
函数的概念与性质
第三章
3.4 函数的应用(一)
课程标准 核心素养
理解函数模型是描述客观世界中变量关系和规律的重要数学语言和工具.在实际情境中,会选择合适的函数类型刻画现实问题的变化规律. 通过对函数的应用(一)的学习,提升“数学建模”、“逻辑推理”、“数学运算”的核心素养.
栏目索引
课堂互动探究
随堂本课小结
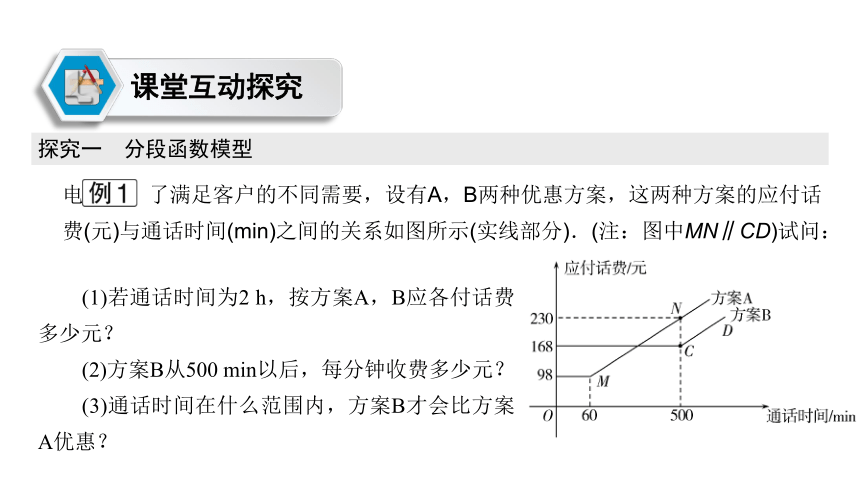
电信局为了满足客户的不同需要,设有A,B两种优惠方案,这两种方案的应付话费(元)与通话时间(min)之间的关系如图所示(实线部分).(注:图中MN∥CD)试问:
课堂互动探究
探究一 分段函数模型
(1)若通话时间为2 h,按方案A,B应各付话费多少元?
(2)方案B从500 min以后,每分钟收费多少元?
(3)通话时间在什么范围内,方案B才会比方案A优惠?
[方法总结]
1.一次函数模型的特点和求解方法
(1)一次函数模型的突出特点是其图象是一条直线.
(2)解一次函数模型时,注意待定系数法的应用,主要步骤是:设元、列式、求解.
2.分段函数模型应用的两个注意点
(1)分段对待:分段函数主要是每一段自变量变化所遵循的规律不同,可以先将其当成几个问题,将各段的变化规律分别找出来,再将其合到一起,要注意各段自变量的取值范围,特别是端点值.
(2)原则:构造分段函数时,要力求准确、简洁,做到分段合理、不重不漏.
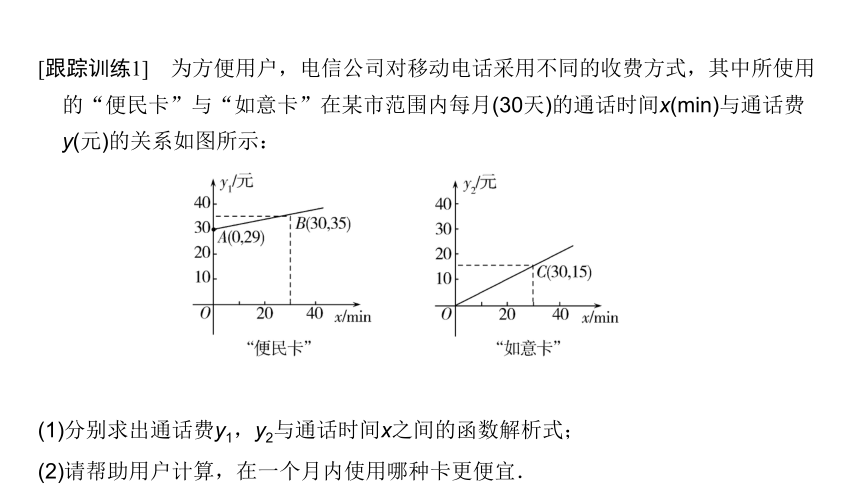
[跟踪训练1] 为方便用户,电信公司对移动电话采用不同的收费方式,其中所使用的“便民卡”与“如意卡”在某市范围内每月(30天)的通话时间x(min)与通话费y(元)的关系如图所示:
(1)分别求出通话费y1,y2与通话时间x之间的函数解析式;
(2)请帮助用户计算,在一个月内使用哪种卡更便宜.
牧场中羊群的最大蓄养量为m只,为保证羊群的生长空间,实际蓄养量不能达到最大蓄养量,必须留出适当的空闲率.已知羊群的年增长量y只和实际蓄养量x只与空闲率的乘积成正比,比例系数为k(k>0).
(1)写出y关于x的函数关系式,并指出这个函数的定义域;
(2)求羊群年增长量的最大值;
(3)当羊群的年增长量达到最大值时,求k的取值范围.
探究二 二次函数模型
[变式探究] 若将本例“与空闲率的乘积成正比”改为“与空闲率的乘积成反比”,又如何表示出y关于x的函数关系式?
[方法总结]
利用二次函数求最值的方法及注意点
方法:根据实际问题建立函数模型解析式后,可利用配方法、判别式法、换元法利用函数的单调性等方法求最值,从而解决实际问题中的利润最大、用料最省等最值问题.
注意点:取得最值时的自变量与实际意义是否相符.
[跟踪训练2] 据市场分析,某海鲜加工公司,当月产量在10吨至25吨时,月生产总成本y(万元)可以看成月产量x(吨)的二次函数;当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元,为二次函数的顶点.
(1)写出月总成本y(万元)关于月产量x(吨)的函数关系式;
(2)已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获得最大利润.
某药厂研制出一种新型药剂,投放市场后其广告投入x(万元)与药品利润y(万元)存在的关系为y=xα(α为常数),其中x不超过5万元,已知去年投入广告费用为3万元时,药品利润为27万元,若今年广告费用投入5万元,预计今年药品利润为________万元.
解析 由已知投入广告费用为3万元时,药品利润为27万元,代入y= xα中,即3α=27,解得α=3,故函数解析式为y=x3,所以当x=5时,y=125.
答案 125
探究三 幂函数模型应用举例
[方法总结]
处理幂函数模型的步骤
(1)阅读理解、认真审题.
(2)用数学符号表示相关量,列出函数解析式.
(3)根据幂函数的性质推导运算,求得结果.
(4)转化成具体问题,给出解答.
[跟踪训练3] 某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元.
(1)分别写出两类产品的收益与投资额的函数关系;
(2)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
建立数学模型一定要过好三关:
(1)事理关:通过阅读、理解,明白问题讲的是什么,熟悉实际背景,为解题打开突破口.
(2)文理关:将实际问题的文字语言转化为数学的符号语言,用数学式子表达文字关系.
(3)数理关:在构建数学模型的过程中,对已知数学知识进行检索,从而认定或构建相应的数学模型.
随堂本课小结
函数的概念与性质
第三章
3.4 函数的应用(一)
课程标准 核心素养
理解函数模型是描述客观世界中变量关系和规律的重要数学语言和工具.在实际情境中,会选择合适的函数类型刻画现实问题的变化规律. 通过对函数的应用(一)的学习,提升“数学建模”、“逻辑推理”、“数学运算”的核心素养.
栏目索引
课堂互动探究
随堂本课小结
电信局为了满足客户的不同需要,设有A,B两种优惠方案,这两种方案的应付话费(元)与通话时间(min)之间的关系如图所示(实线部分).(注:图中MN∥CD)试问:
课堂互动探究
探究一 分段函数模型
(1)若通话时间为2 h,按方案A,B应各付话费多少元?
(2)方案B从500 min以后,每分钟收费多少元?
(3)通话时间在什么范围内,方案B才会比方案A优惠?
[方法总结]
1.一次函数模型的特点和求解方法
(1)一次函数模型的突出特点是其图象是一条直线.
(2)解一次函数模型时,注意待定系数法的应用,主要步骤是:设元、列式、求解.
2.分段函数模型应用的两个注意点
(1)分段对待:分段函数主要是每一段自变量变化所遵循的规律不同,可以先将其当成几个问题,将各段的变化规律分别找出来,再将其合到一起,要注意各段自变量的取值范围,特别是端点值.
(2)原则:构造分段函数时,要力求准确、简洁,做到分段合理、不重不漏.
[跟踪训练1] 为方便用户,电信公司对移动电话采用不同的收费方式,其中所使用的“便民卡”与“如意卡”在某市范围内每月(30天)的通话时间x(min)与通话费y(元)的关系如图所示:
(1)分别求出通话费y1,y2与通话时间x之间的函数解析式;
(2)请帮助用户计算,在一个月内使用哪种卡更便宜.
牧场中羊群的最大蓄养量为m只,为保证羊群的生长空间,实际蓄养量不能达到最大蓄养量,必须留出适当的空闲率.已知羊群的年增长量y只和实际蓄养量x只与空闲率的乘积成正比,比例系数为k(k>0).
(1)写出y关于x的函数关系式,并指出这个函数的定义域;
(2)求羊群年增长量的最大值;
(3)当羊群的年增长量达到最大值时,求k的取值范围.
探究二 二次函数模型
[变式探究] 若将本例“与空闲率的乘积成正比”改为“与空闲率的乘积成反比”,又如何表示出y关于x的函数关系式?
[方法总结]
利用二次函数求最值的方法及注意点
方法:根据实际问题建立函数模型解析式后,可利用配方法、判别式法、换元法利用函数的单调性等方法求最值,从而解决实际问题中的利润最大、用料最省等最值问题.
注意点:取得最值时的自变量与实际意义是否相符.
[跟踪训练2] 据市场分析,某海鲜加工公司,当月产量在10吨至25吨时,月生产总成本y(万元)可以看成月产量x(吨)的二次函数;当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元,为二次函数的顶点.
(1)写出月总成本y(万元)关于月产量x(吨)的函数关系式;
(2)已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获得最大利润.
某药厂研制出一种新型药剂,投放市场后其广告投入x(万元)与药品利润y(万元)存在的关系为y=xα(α为常数),其中x不超过5万元,已知去年投入广告费用为3万元时,药品利润为27万元,若今年广告费用投入5万元,预计今年药品利润为________万元.
解析 由已知投入广告费用为3万元时,药品利润为27万元,代入y= xα中,即3α=27,解得α=3,故函数解析式为y=x3,所以当x=5时,y=125.
答案 125
探究三 幂函数模型应用举例
[方法总结]
处理幂函数模型的步骤
(1)阅读理解、认真审题.
(2)用数学符号表示相关量,列出函数解析式.
(3)根据幂函数的性质推导运算,求得结果.
(4)转化成具体问题,给出解答.
[跟踪训练3] 某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元.
(1)分别写出两类产品的收益与投资额的函数关系;
(2)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
建立数学模型一定要过好三关:
(1)事理关:通过阅读、理解,明白问题讲的是什么,熟悉实际背景,为解题打开突破口.
(2)文理关:将实际问题的文字语言转化为数学的符号语言,用数学式子表达文字关系.
(3)数理关:在构建数学模型的过程中,对已知数学知识进行检索,从而认定或构建相应的数学模型.
随堂本课小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
