4.3.2 对数的运算 课件(共22张PPT)
文档属性
| 名称 | 4.3.2 对数的运算 课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 856.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-25 04:47:12 | ||
图片预览





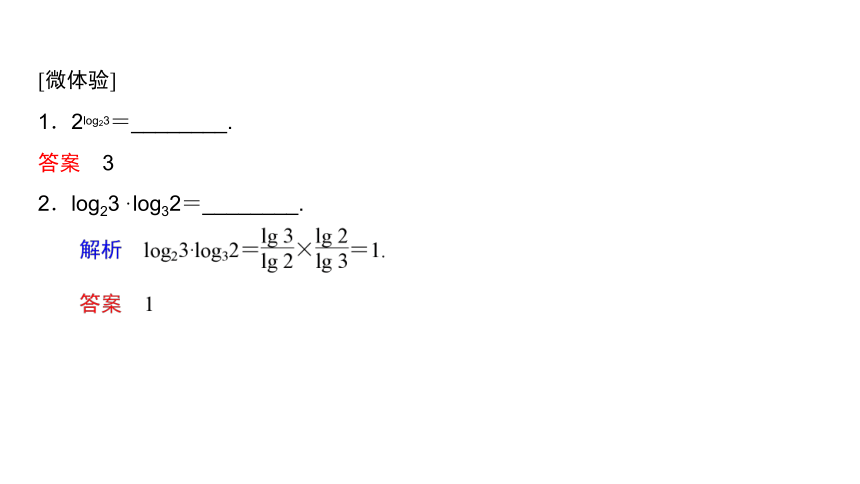


文档简介
(共22张PPT)
指数函数与对数函数
第四章
4.3.2 对数的运算
4.3 对数
栏目索引
课前自主预习
课堂互动探究
随堂本课小结
课前自主预习
知识点1 对数的运算性质
logaM+logaN
logaM-logaN
nlogaM
[微思考]
1.运算性质中底数a能等于零或小于零吗,真数M,N呢?
提示:由对数的定义知底数a>0且a≠1,故a不能小于或等于0,M,N均为正数.
2.当M>0,N>0时,loga(M+N)=logaM+logaN,loga(MN)=logaM·logaN是否成立?
提示:不一定.
知识点2 对数的换底公式与对数恒等式
logab
1
N
[微体验]
1.2log23=________.
答案 3
2.log23·log32=________.
3.若lg 3=a,lg 2=b,用a,b表示log43=________.
课堂互动探究
探究一 对数恒等式的应用
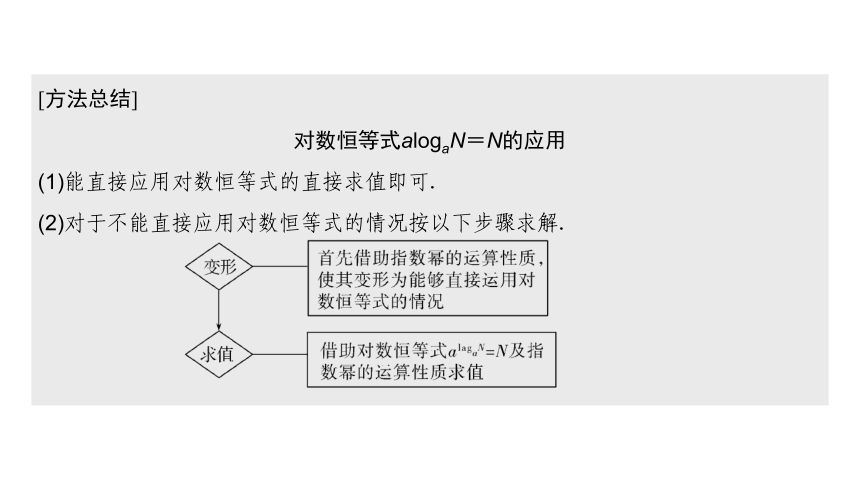
[方法总结]
对数恒等式alogaN=N的应用
(1)能直接应用对数恒等式的直接求值即可.
(2)对于不能直接应用对数恒等式的情况按以下步骤求解.
探究二 对数运算性质的运用
[方法总结]
底数相同的对数式的化简和求值的原则、方法及注意事项
(1)基本原则.
对数的化简、求值一般是正用或逆用公式,对真数进行处理,选哪种策略化简,取决于问题的实际情况,一般本着便于真数化简的原则进行.
(2)两种常用方法.
①“收”,将同底的两对数的和(差)收成积(商)的对数.
②“拆”,将积(商)的对数拆成同底的两对数的和(差).
(3)注意事项.
①对于常用对数的化简要充分利用“lg 5+lg 2=lg 10=1”解题.
②准确应用以下结论:
loga1=0,logaa=1,alogaN=N(a>0,且a≠1,N>0).
探究三 对数换底公式
[变式探究1] 本例条件不变,试用a,b表示log2898.
[变式探究2] 若把本例中条件“2b=3”换为3b=2,其他条件不变,则结论又如何呢?
[方法总结]
1.利用换底公式化简、求值时应注意的问题
(1)针对具体问题,选择恰当的底数.
(2)注意换底公式与对数运算法则结合使用.
(3)换底公式的正用与逆用.
(4)恰当应用换底公式的两个常用结论.
2.利用换底公式计算、化简、求值的思路
[跟踪训练3] 已知log23=a,log37=b,用a,b表示log4256.
随堂本课小结
(2)利用对数的运算性质可以把乘、除、乘方的运算转化为对数的加、减、乘运算,反之亦然.
(3)对于每一条运算性质,都要注意只有当式子中所有的对数都有意义时,等式才成立.
3.利用换底公式可以把题目中不同底的对数化成同底的对数,进一步应用对数运算的性质.
指数函数与对数函数
第四章
4.3.2 对数的运算
4.3 对数
栏目索引
课前自主预习
课堂互动探究
随堂本课小结
课前自主预习
知识点1 对数的运算性质
logaM+logaN
logaM-logaN
nlogaM
[微思考]
1.运算性质中底数a能等于零或小于零吗,真数M,N呢?
提示:由对数的定义知底数a>0且a≠1,故a不能小于或等于0,M,N均为正数.
2.当M>0,N>0时,loga(M+N)=logaM+logaN,loga(MN)=logaM·logaN是否成立?
提示:不一定.
知识点2 对数的换底公式与对数恒等式
logab
1
N
[微体验]
1.2log23=________.
答案 3
2.log23·log32=________.
3.若lg 3=a,lg 2=b,用a,b表示log43=________.
课堂互动探究
探究一 对数恒等式的应用
[方法总结]
对数恒等式alogaN=N的应用
(1)能直接应用对数恒等式的直接求值即可.
(2)对于不能直接应用对数恒等式的情况按以下步骤求解.
探究二 对数运算性质的运用
[方法总结]
底数相同的对数式的化简和求值的原则、方法及注意事项
(1)基本原则.
对数的化简、求值一般是正用或逆用公式,对真数进行处理,选哪种策略化简,取决于问题的实际情况,一般本着便于真数化简的原则进行.
(2)两种常用方法.
①“收”,将同底的两对数的和(差)收成积(商)的对数.
②“拆”,将积(商)的对数拆成同底的两对数的和(差).
(3)注意事项.
①对于常用对数的化简要充分利用“lg 5+lg 2=lg 10=1”解题.
②准确应用以下结论:
loga1=0,logaa=1,alogaN=N(a>0,且a≠1,N>0).
探究三 对数换底公式
[变式探究1] 本例条件不变,试用a,b表示log2898.
[变式探究2] 若把本例中条件“2b=3”换为3b=2,其他条件不变,则结论又如何呢?
[方法总结]
1.利用换底公式化简、求值时应注意的问题
(1)针对具体问题,选择恰当的底数.
(2)注意换底公式与对数运算法则结合使用.
(3)换底公式的正用与逆用.
(4)恰当应用换底公式的两个常用结论.
2.利用换底公式计算、化简、求值的思路
[跟踪训练3] 已知log23=a,log37=b,用a,b表示log4256.
随堂本课小结
(2)利用对数的运算性质可以把乘、除、乘方的运算转化为对数的加、减、乘运算,反之亦然.
(3)对于每一条运算性质,都要注意只有当式子中所有的对数都有意义时,等式才成立.
3.利用换底公式可以把题目中不同底的对数化成同底的对数,进一步应用对数运算的性质.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
