1.1任意角的概念与弧度制
图片预览






文档简介
课件15张PPT。任意角的概念与
弧度制习题课
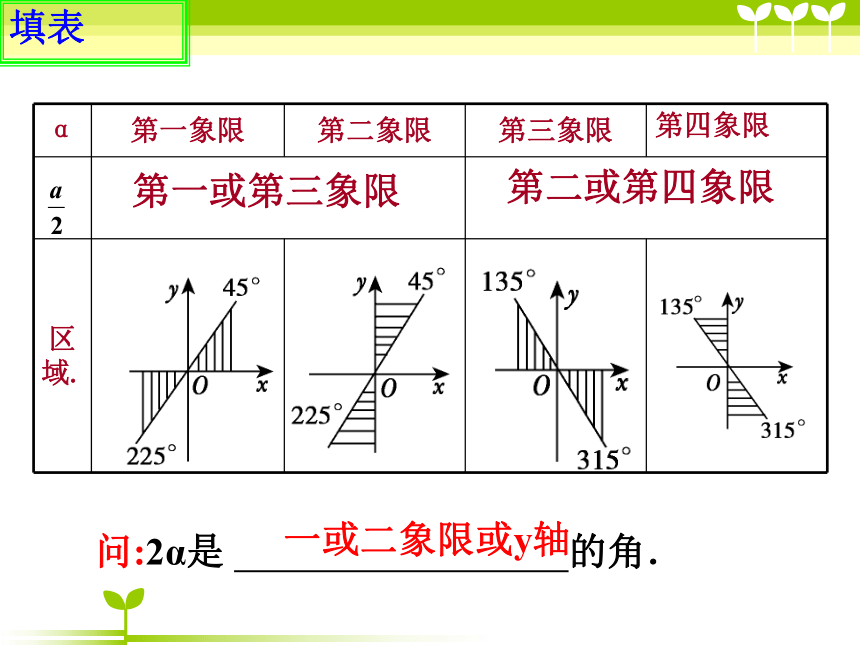
问:2α是 的角.填表第一或第三象限
第二或第四象限
一或二象限或y轴1. 在半径为R的圆中,240o的中心角所对的弧长为 ,面积为2R2的扇形的中心角等于 弧度.解:(1)240o= ,根据l=αR,得(2)根据S= lR= αR2,且S=2R2.所以 α=4.练一练42. 已知一半径为R的扇形,它的周长等于所在圆的周长,那么扇形的中心角是多少弧度?合多少度?扇形的面积是多少? 解:周长=2πR=2R+l,所以l=2(π-1)R.所以扇形的中心角是2(π-1) rad.合( ) o扇形面积是练一练返回目录 *对应演练*(1)∵α=120°= rad,r=6,
∴AB的弧长为l= ×6=4π.
(2)∵S扇形OAB = lr= ×4π×6=12π,
S△ABO = r2·sin = ×62× = ,
∴S 弓形OAB =S 扇形OAB –S △ABO =12π- .已知扇形OAB的圆心角α为120°,半径长为6.
(1) 求AB的弧长;
(2) 求弓形OAB的面积.︵︵返回目录 3.已知一扇形的中心角是α,所在圆的半径是R.
若扇形的周长是一定值c(c>0),当α为多少
弧度时,该扇形有最大面积?练一练 解:设扇形弧长为L,面积为S 则2R+L=c, ∴L=c-2R 答:当扇形圆心角为2弧度时,扇形面积有最大值.……3.已知一扇形的中心角是α,所在圆的半径是R.
若扇形的周长是一定值c(c>0),当α为多少
弧度时,该扇形有最大面积? ∵扇形周长c=2R+l=2R+αR, 练一练4.与角-1825o的终边相同,且绝对值最小的角的度数是___,合___弧度。 解:-1825o=-5×360o-25o, 所以与角-1825o的终边相同,且绝对值最小的角是-25o.合练一练5.若角α的终边在图2-4中所表示的范围内,
则α∈ . (k·360°-210°,k·360°+30°)
其中 k∈Z练一练7.已知0正半轴重合,则角α与角α+π的终边的关系是?????
A.一定关于x轴对称
B.一定关于y轴对称
C.可能关于原点不对称
D.随α的变化可以有不同的对称性√12.设α、β满足-180°<α<β<180°,
则α-β的范围是??????
A.-360°<α-β<0°
B.-180°<α-β<180°
C.-180°<α-β<0°
D.-360°<α-β<360°11.设A={θ|θ为正锐角},
B={θ|θ为小于90°的角},
C={θ|θ为第一象限的角},
D={θ|θ为小于90°的正角},
则下列等式中成立的是?????????????????????????????
A.A=B?????? B.B=C C.A=C??????? D.A=D√√1.β的终边与60o角的终边相同,在[0o,360o]范围内,求终边与角 的终边相同的角?作 业2.用α表示β,若α,β终边关于直线(1)y=x(2)y=x对称3.若90o<β<α<135o,求α+β,α-β的范围4.求下列两集合间的交集作业解:β=k·360o+60o,k∈Z.所以 =k·120o+20o, k∈Z.当k=0时,得角为20o,当k=1时,得角为140o,当k=2时,得角为260o.1.β的终边与60o角的终边相同,在[0o,360o]范围内,求终边与角 的终边相同的角?3、若90o<β<α<135o,则α-β的范围是__________,α+β的范围是___________;(0o,45o)(180o,270o)2.用α表示β,若α,β终边关于直线(1)y=x(2)y=x对称
弧度制习题课
问:2α是 的角.填表第一或第三象限
第二或第四象限
一或二象限或y轴1. 在半径为R的圆中,240o的中心角所对的弧长为 ,面积为2R2的扇形的中心角等于 弧度.解:(1)240o= ,根据l=αR,得(2)根据S= lR= αR2,且S=2R2.所以 α=4.练一练42. 已知一半径为R的扇形,它的周长等于所在圆的周长,那么扇形的中心角是多少弧度?合多少度?扇形的面积是多少? 解:周长=2πR=2R+l,所以l=2(π-1)R.所以扇形的中心角是2(π-1) rad.合( ) o扇形面积是练一练返回目录 *对应演练*(1)∵α=120°= rad,r=6,
∴AB的弧长为l= ×6=4π.
(2)∵S扇形OAB = lr= ×4π×6=12π,
S△ABO = r2·sin = ×62× = ,
∴S 弓形OAB =S 扇形OAB –S △ABO =12π- .已知扇形OAB的圆心角α为120°,半径长为6.
(1) 求AB的弧长;
(2) 求弓形OAB的面积.︵︵返回目录 3.已知一扇形的中心角是α,所在圆的半径是R.
若扇形的周长是一定值c(c>0),当α为多少
弧度时,该扇形有最大面积?练一练 解:设扇形弧长为L,面积为S 则2R+L=c, ∴L=c-2R 答:当扇形圆心角为2弧度时,扇形面积有最大值.……3.已知一扇形的中心角是α,所在圆的半径是R.
若扇形的周长是一定值c(c>0),当α为多少
弧度时,该扇形有最大面积? ∵扇形周长c=2R+l=2R+αR, 练一练4.与角-1825o的终边相同,且绝对值最小的角的度数是___,合___弧度。 解:-1825o=-5×360o-25o, 所以与角-1825o的终边相同,且绝对值最小的角是-25o.合练一练5.若角α的终边在图2-4中所表示的范围内,
则α∈ . (k·360°-210°,k·360°+30°)
其中 k∈Z练一练7.已知0
A.一定关于x轴对称
B.一定关于y轴对称
C.可能关于原点不对称
D.随α的变化可以有不同的对称性√12.设α、β满足-180°<α<β<180°,
则α-β的范围是??????
A.-360°<α-β<0°
B.-180°<α-β<180°
C.-180°<α-β<0°
D.-360°<α-β<360°11.设A={θ|θ为正锐角},
B={θ|θ为小于90°的角},
C={θ|θ为第一象限的角},
D={θ|θ为小于90°的正角},
则下列等式中成立的是?????????????????????????????
A.A=B?????? B.B=C C.A=C??????? D.A=D√√1.β的终边与60o角的终边相同,在[0o,360o]范围内,求终边与角 的终边相同的角?作 业2.用α表示β,若α,β终边关于直线(1)y=x(2)y=x对称3.若90o<β<α<135o,求α+β,α-β的范围4.求下列两集合间的交集作业解:β=k·360o+60o,k∈Z.所以 =k·120o+20o, k∈Z.当k=0时,得角为20o,当k=1时,得角为140o,当k=2时,得角为260o.1.β的终边与60o角的终边相同,在[0o,360o]范围内,求终边与角 的终边相同的角?3、若90o<β<α<135o,则α-β的范围是__________,α+β的范围是___________;(0o,45o)(180o,270o)2.用α表示β,若α,β终边关于直线(1)y=x(2)y=x对称
