26.3 圆的确定
图片预览





文档简介
课件18张PPT。人有悲欢离合,月有阴晴圆缺
---宋·苏轼破镜重圆从古有,何须疑虑反生愁?
——元·施君美《幽闺记·推就红丝》 唐朝的铜镜是中国铜镜中的精品。江西省文物考古研究所日前从玉山县一座唐代墓葬中出土了半面铜镜,那么你有什么方法使得它能“破镜重圆”呢? 池州市东至县官港中学
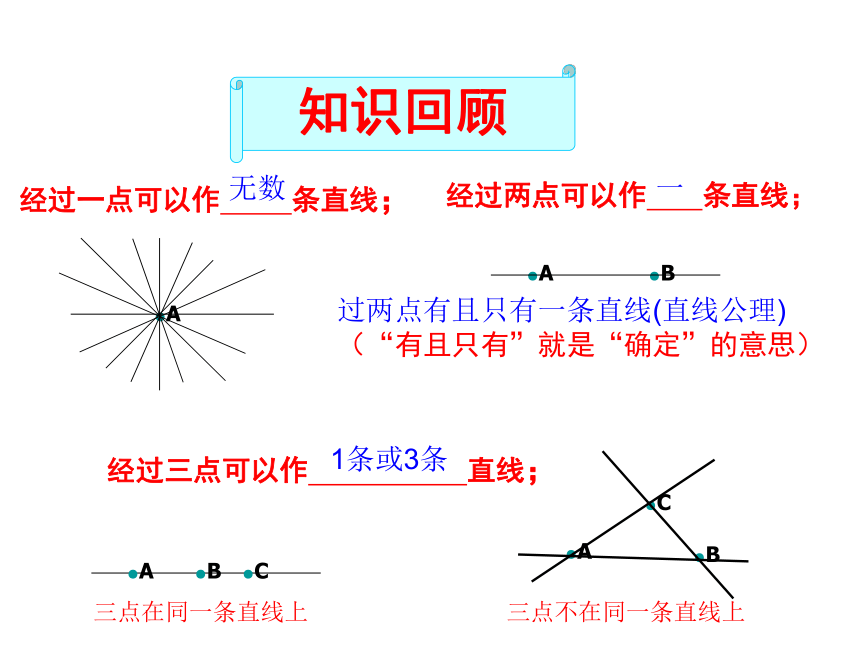
陈远军25.3 圆的确定●A●A●B经过一点可以作 条直线;过两点有且只有一条直线(直线公理)
(“有且只有”就是“确定”的意思)
经过两点可以作 条直线;经过三点可以作 直线;●A●B●C●A●B●C无数一1条或3条三点在同一条直线上三点不在同一条直线上过一点可以作几个圆?过两点?
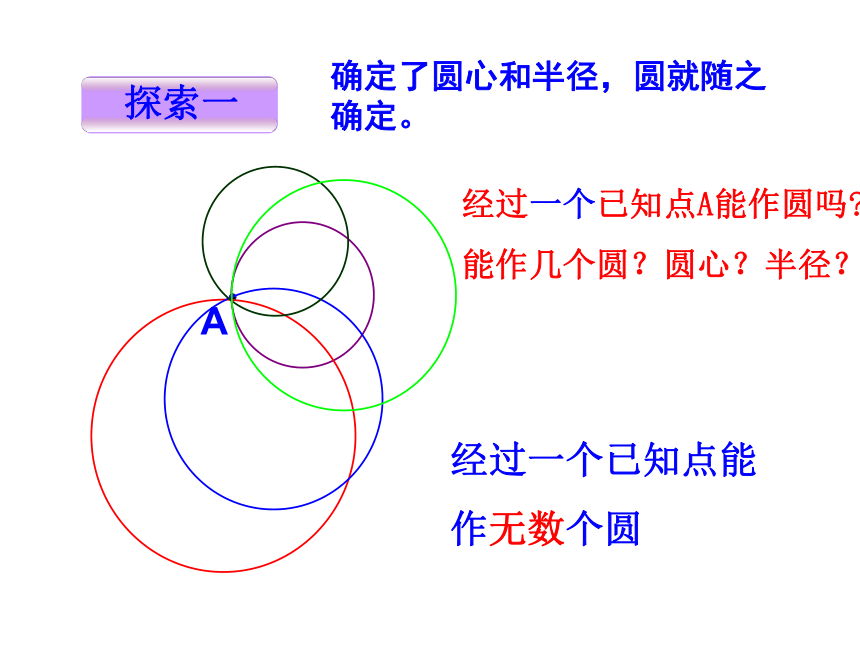
过三点呢?经过一个已知点A能作圆吗?
能作几个圆?圆心?半径?A经过一个已知点能 作无数个圆确定了圆心和半径,圆就随之确定。 经过两个已知点A、B能作圆吗?圆心?半径?AB 经过两个已知点A、B能作无数个圆 它们的圆心都在线段AB的中垂线上。 1. 经过不在同一条直线上的三个已知点A、B、C能作圆吗? 假设经过A、B、C三点的⊙O存在(1)圆心O到A、B、C三点距离
。(2)点O在AB的 上;
点O又在AC的 上;
点O是线段AB、AC的____________的________ 。 ABC相等垂直平分线垂直平分线交点 经过三个已知点A、B、C能作圆吗?圆心?半径?垂直平分线已知:不在同一直线上的三点A、B、C
求作: ⊙O,使它经过点A、B、C作法:1、连接AB,作线段AB的垂直平分线MN;
2、连接AC,作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆。所以⊙O就是所求作的圆。ONMFEABC不在同一条直线上的三个点确定一个圆。 经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形。如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心 外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等。 一个圆的内接三角形有几个?
一个三角形的外接圆有几个?△ABC与⊙O的关系下列命题不正确的是
A.三角形的外心到三个顶点的距离相等.
B.直角三角形的外心必在它的斜边上
C.圆只有一个内接三角形.
D.过不在同一直线上三点能作一个圆C 某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等。请问同学们这所中学建在哪个位置?你怎么确定这个位置吗?●●●BAC如图,点O是△ABC的外心,求∠1+∠2+∠3的度数。123 如何解决“破镜重圆”的问题:圆心一定在弦的垂直平分线上方法:
1、在圆弧上任取三点A、B、C。
2、作线段AB、BC的垂直平分线,其交点O即为圆心。
3、以点O为圆心,OC长为半径作圆。
⊙O即为所求。今天你有什么收获?(1)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定
(2)经过一个已知点能作无数个圆;经过两个已知点A、B能作无数个圆,
这些圆 的圆心在线段AB的垂直平分线上。
(3)不在同一直线上的三个点确定一个圆。
(4)三角形的外接圆,外心的概念。
(5)三角形的外心到三角形三个顶点的距离相等。1. 新知识:2.数学方法和思想类比方法和归纳思想1.课堂作业:
课本P26页第2题2.思考:
过如下三点能不能做一个圆? 为什么?如何证明?ABC锐角三角形的外心位于三角形内部.
直角三角形的外心位于直角三角形斜边中点.
钝角三角形的外心位于三角形外部. 在学案上分别画出一个锐角三角形、直角三角形和钝角三角形的外接圆,观察并叙述各三角形与它的外心的位置关系.
——元·施君美《幽闺记·推就红丝》 唐朝的铜镜是中国铜镜中的精品。江西省文物考古研究所日前从玉山县一座唐代墓葬中出土了半面铜镜,那么你有什么方法使得它能“破镜重圆”呢? 池州市东至县官港中学
陈远军25.3 圆的确定●A●A●B经过一点可以作 条直线;过两点有且只有一条直线(直线公理)
(“有且只有”就是“确定”的意思)
经过两点可以作 条直线;经过三点可以作 直线;●A●B●C●A●B●C无数一1条或3条三点在同一条直线上三点不在同一条直线上过一点可以作几个圆?过两点?
过三点呢?经过一个已知点A能作圆吗?
能作几个圆?圆心?半径?A经过一个已知点能 作无数个圆确定了圆心和半径,圆就随之确定。 经过两个已知点A、B能作圆吗?圆心?半径?AB 经过两个已知点A、B能作无数个圆 它们的圆心都在线段AB的中垂线上。 1. 经过不在同一条直线上的三个已知点A、B、C能作圆吗? 假设经过A、B、C三点的⊙O存在(1)圆心O到A、B、C三点距离
。(2)点O在AB的 上;
点O又在AC的 上;
点O是线段AB、AC的____________的________ 。 ABC相等垂直平分线垂直平分线交点 经过三个已知点A、B、C能作圆吗?圆心?半径?垂直平分线已知:不在同一直线上的三点A、B、C
求作: ⊙O,使它经过点A、B、C作法:1、连接AB,作线段AB的垂直平分线MN;
2、连接AC,作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆。所以⊙O就是所求作的圆。ONMFEABC不在同一条直线上的三个点确定一个圆。 经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形。如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心 外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等。 一个圆的内接三角形有几个?
一个三角形的外接圆有几个?△ABC与⊙O的关系下列命题不正确的是
A.三角形的外心到三个顶点的距离相等.
B.直角三角形的外心必在它的斜边上
C.圆只有一个内接三角形.
D.过不在同一直线上三点能作一个圆C 某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等。请问同学们这所中学建在哪个位置?你怎么确定这个位置吗?●●●BAC如图,点O是△ABC的外心,求∠1+∠2+∠3的度数。123 如何解决“破镜重圆”的问题:圆心一定在弦的垂直平分线上方法:
1、在圆弧上任取三点A、B、C。
2、作线段AB、BC的垂直平分线,其交点O即为圆心。
3、以点O为圆心,OC长为半径作圆。
⊙O即为所求。今天你有什么收获?(1)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定
(2)经过一个已知点能作无数个圆;经过两个已知点A、B能作无数个圆,
这些圆 的圆心在线段AB的垂直平分线上。
(3)不在同一直线上的三个点确定一个圆。
(4)三角形的外接圆,外心的概念。
(5)三角形的外心到三角形三个顶点的距离相等。1. 新知识:2.数学方法和思想类比方法和归纳思想1.课堂作业:
课本P26页第2题2.思考:
过如下三点能不能做一个圆? 为什么?如何证明?ABC锐角三角形的外心位于三角形内部.
直角三角形的外心位于直角三角形斜边中点.
钝角三角形的外心位于三角形外部. 在学案上分别画出一个锐角三角形、直角三角形和钝角三角形的外接圆,观察并叙述各三角形与它的外心的位置关系.
