沪科版八年级下册 17.5 一元二次方程的应用课件(故13张PPT)
文档属性
| 名称 | 沪科版八年级下册 17.5 一元二次方程的应用课件(故13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 169.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-24 00:00:00 | ||
图片预览



文档简介
(共13张PPT)
17.5 一元二次方程的应用
一元二次方程的应用
之面积问题
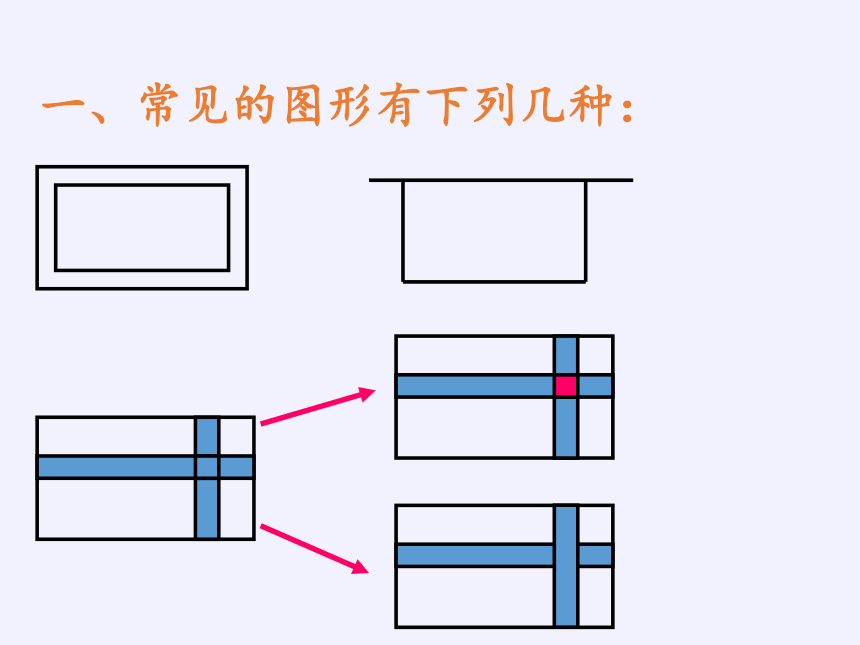
一、常见的图形有下列几种:
5
x
x
x
x
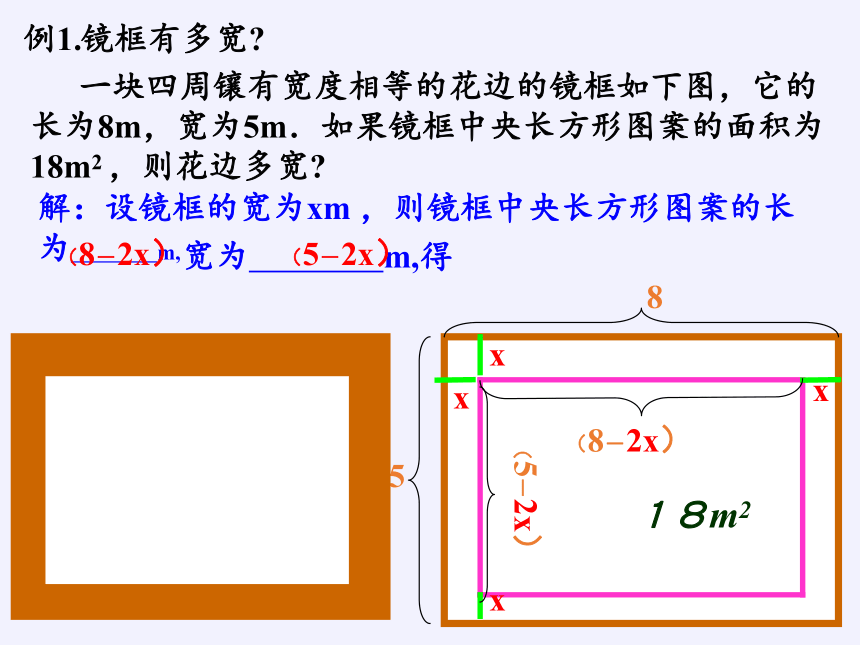
(8-2x)
(5-2x)
8
镜框有多宽
一块四周镶有宽度相等的花边的镜框如下图,它的长为8m,宽为5m.如果镜框中央长方形图案的面积为18m2 ,则花边多宽
解:设镜框的宽为xm ,则镜框中央长方形图案的长为 m,
宽为 m,得
(8-2x)
(5-2x)
18m2
例1.
宽为 m,得
(8 - 2x) (5 - 2x) = 18
镜框有多宽
一块四周镶有宽度相等的花边的镜框如下图,它的长为8m,宽为5m.如果镜框中央长方形图案的面积为18m2 ,则镜框多宽
解:设镜框的宽为xm ,则镜框中央长方形
图案的长为 m,
(8-2x)
(5-2x)
例1.
即2X2 - 13 X + 11=0
解得X1=1,
X2=5.5(不合题意)
答:镜框的宽为1m.
审
设
答
解
列
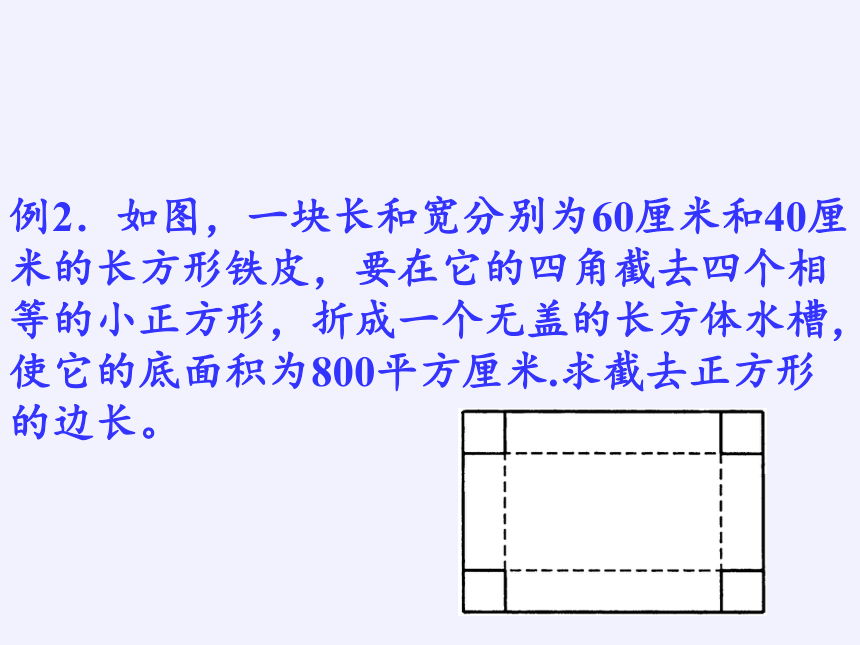
例2.如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方厘米.求截去正方形的边长。
例2.如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方厘米.求截去正方形的边长。
答:截去正方形的边长为10厘米。
例3. 如图,在长为40米,宽为22米的矩形地面上,修筑两条同样宽的互相垂直的道路,余下的铺上草坪,要使草坪的面积为760平方米,道路的宽应为多少?
40米
22米
[例4] 学校要建一个面积为150平方米的长方形自行车棚,为节约经费,一边利用18米长的教学楼后墙,另三边利用总长为35米的铁围栏围成,求自行车棚的长和宽.
解:设与教学楼后墙垂直的一条边长为x米,则与教学
楼后墙平行的那条边长为
(35 2x)米,根据题意,得
x(35 2x) 150
解得
当 时,35 2x 20 18不合题意,舍去;
当x 10时,35 2x 15. 符合题意.
答:自行车棚的长和宽分别为15米和10米.
练习:
4.如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路(两条纵向,一条横向,且互相垂直),把耕地分成六块大小相等的试验地,要使试验地的面积为570平方米,问:道路宽为多少米
解:设道路宽为x米,
则
化简得,
其中的 x=35超出了原矩形的宽,应舍去.
答:道路的宽为1米.
小结:
列一元二次方程解应用题的步骤?
谢 谢
17.5 一元二次方程的应用
一元二次方程的应用
之面积问题
一、常见的图形有下列几种:
5
x
x
x
x
(8-2x)
(5-2x)
8
镜框有多宽
一块四周镶有宽度相等的花边的镜框如下图,它的长为8m,宽为5m.如果镜框中央长方形图案的面积为18m2 ,则花边多宽
解:设镜框的宽为xm ,则镜框中央长方形图案的长为 m,
宽为 m,得
(8-2x)
(5-2x)
18m2
例1.
宽为 m,得
(8 - 2x) (5 - 2x) = 18
镜框有多宽
一块四周镶有宽度相等的花边的镜框如下图,它的长为8m,宽为5m.如果镜框中央长方形图案的面积为18m2 ,则镜框多宽
解:设镜框的宽为xm ,则镜框中央长方形
图案的长为 m,
(8-2x)
(5-2x)
例1.
即2X2 - 13 X + 11=0
解得X1=1,
X2=5.5(不合题意)
答:镜框的宽为1m.
审
设
答
解
列
例2.如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方厘米.求截去正方形的边长。
例2.如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方厘米.求截去正方形的边长。
答:截去正方形的边长为10厘米。
例3. 如图,在长为40米,宽为22米的矩形地面上,修筑两条同样宽的互相垂直的道路,余下的铺上草坪,要使草坪的面积为760平方米,道路的宽应为多少?
40米
22米
[例4] 学校要建一个面积为150平方米的长方形自行车棚,为节约经费,一边利用18米长的教学楼后墙,另三边利用总长为35米的铁围栏围成,求自行车棚的长和宽.
解:设与教学楼后墙垂直的一条边长为x米,则与教学
楼后墙平行的那条边长为
(35 2x)米,根据题意,得
x(35 2x) 150
解得
当 时,35 2x 20 18不合题意,舍去;
当x 10时,35 2x 15. 符合题意.
答:自行车棚的长和宽分别为15米和10米.
练习:
4.如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路(两条纵向,一条横向,且互相垂直),把耕地分成六块大小相等的试验地,要使试验地的面积为570平方米,问:道路宽为多少米
解:设道路宽为x米,
则
化简得,
其中的 x=35超出了原矩形的宽,应舍去.
答:道路的宽为1米.
小结:
列一元二次方程解应用题的步骤?
谢 谢
