沪科版数学八年级下册 19.4 综合与实践 多边形的镶嵌 课件(共37张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 19.4 综合与实践 多边形的镶嵌 课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 916.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-25 08:18:51 | ||
图片预览








文档简介
(共37张PPT)
19.4 综合与实践 多边形的镶嵌
19.4 综合与实践
多边形的镶嵌
上课教师:施佑新
上课时间:2019.5.28
定义: 用形状相同或不同的
平面封闭图形,覆盖平面区域,
使图形间既无缝隙又不重叠地
全部覆盖,在几何里面叫做平
面镶嵌.
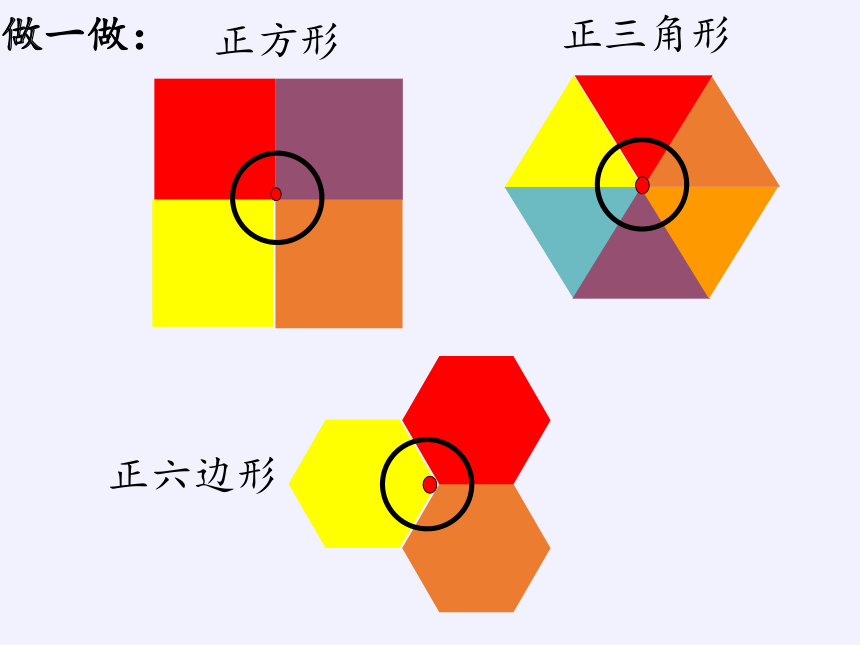
探究1:仅用一种正多边形镶嵌,哪些正多边形能单独镶嵌成一个平面图案?
正方形
正三角形
正六边形
做一做:
要用正多边形镶嵌成一个平面, 关键是:这种正多边形内角的度数能整除360°。
镶嵌满足的条件:
能铺满地面的多边形,围绕某
一点的内角和为( )
思考:什么样的正多边形能够进行镶嵌
360°
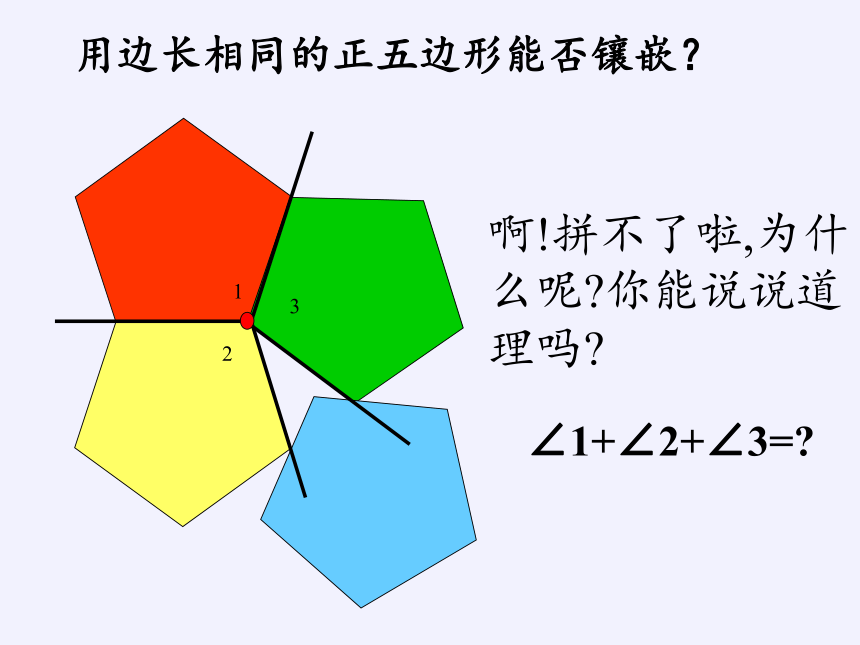
啊!拼不了啦,为什么呢 你能说说道理吗
1
2
3
∠1+∠2+∠3=
用边长相同的正五边形能否镶嵌?
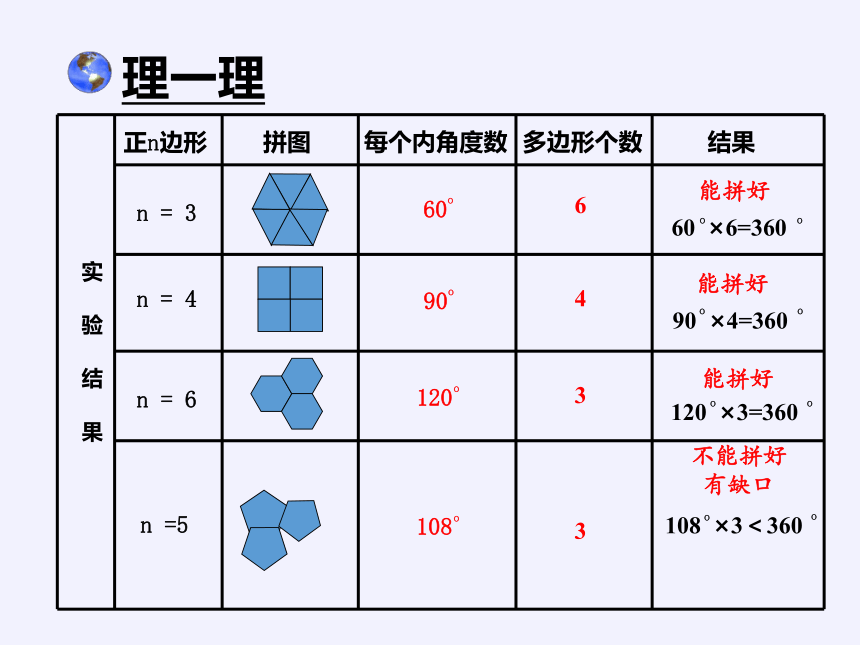
理一理
6
60
o
90
o
108
o
120
o
4
3
3
能拼好
能拼好
不能拼好
有缺口
能拼好
60 ×6=360
o
o
90 ×4=360
o
o
108 ×3<360
o
o
120 ×3=360
o
o
实 验 结 果
正n边形
拼图
每个内角度数
多边形个数
结果
n = 3
n = 4
n =5
n = 6
还能找到能镶嵌的其他正多边形吗?
。
k ·
(n-2)×180
n
= 360
。
(n-2)(k-2)=4
k=6
n=3
k=4
n=4
k=3
n=6
设在一个顶点周围有 k 个正 n 边形的角,则有
∵ k 为正整数, n 为大于等于 3 的正整数
∴解为
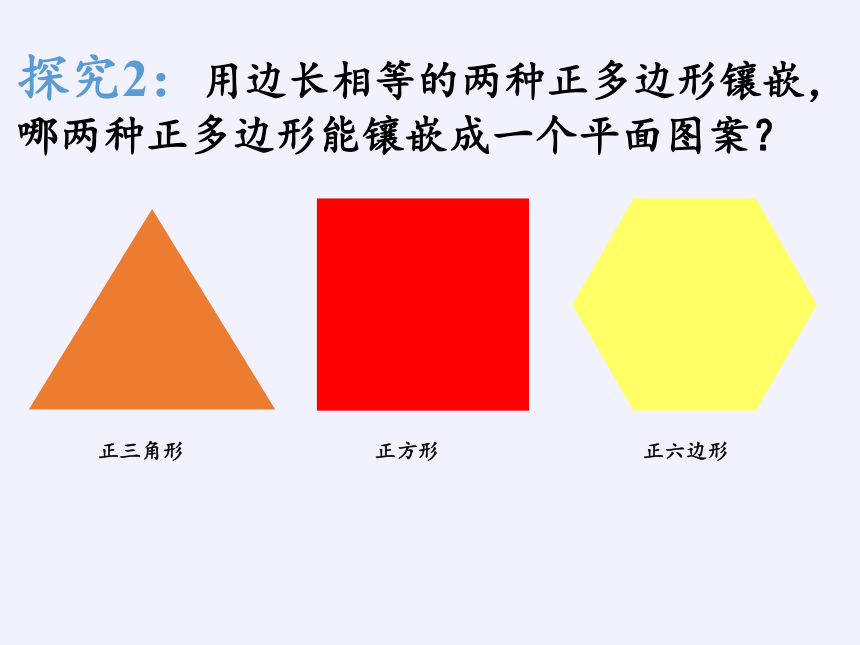
探究2:用边长相等的两种正多边形镶嵌,哪两种正多边形能镶嵌成一个平面图案?
正三角形
正方形
正六边形
60°×3+90°×2=360°
正三角形和正方形
(一)正三角形与正方形
2 m+3 n=12
m=3
n=2
m·60°+n·90° =360°
设在一个顶点周围有 m 个正三角形的角,n 个正方形的角,则有
∵ m,n 为正整数
∴解为
正三角形和正六边形
60°×4 + 120°=360°
60°×2+120°×2=360°
(二)正三角形与正六边形
m+2n=6
m=2
n=2
m=4
n=1
m·60°+n·120 °=360°
设在一个顶点周围有 m 个正三角形的角,n 个正六
边形的角,则有
∵ m,n 为正整数
∴解为
想一想
正方形和正八边形能否镶嵌
正三角形和正十二边形能否镶嵌
你能说出其中的道理吗?
135°
135°
90°
150°
150°
60°
正方形和正八边形
正三角形和正十二边形
正方形和正六边形能否镶嵌
www..cn
正方形和正六边形
用两种正多边形进行镶嵌应满足什么条件 ?
当围绕一点拼在一起的两种正多边形的内角加在一起恰好组成一个周角时,这两种正多边形就能镶嵌.
规律:
正五边形、正十边形
围绕一点能拼成360 ,但能扩展到整个平面,即铺满地面吗?
尽管能围绕一点拼成360 ,但不能扩展到整个平面.
结论:用两种正多边形进行平面镶嵌, 有以下五种可能:
(3个)正三角形+(2个)正方形
(4个)正三角形+(1个)正六边形
(2个)正三角形+(2个)正六边形
(1个)正三角形+(2个)正十二边形
(1个)正方形 + (2个)正八边形
正十二边形与正方形、正五边形的平面镶嵌
思考:用三种以上不同正多边形可以作平面
镶嵌吗?
正三角形与正方形、正六边形的平面镶嵌
探究3:
用几个形状、大小相同的任意三角形能镶嵌成一个平面图案吗?四边形呢?
1
3
2
1
4
3
2
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
(一)同一种任意三角形的镶嵌
结论:形状、大小完全相同的任意三角形能镶嵌成平面图形。
通过探究我发现:
1.任意形状、大小相同的三角形都____镶嵌,
2.在每个拼接点处有___个角,而这___个角的和恰好是这个三角形的内角和的___倍,也就是它们的和为____.
可以
六
六
两
360o
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
(二)同一种任意四角形的镶嵌
结论:形状、大小相同的任意四边形能镶嵌成平面图形。
通过探究我发现:
1.任意形状大小相同的四边形__ _镶嵌.
2.在每个拼接点处有___个角,而这___个角的和恰好是这个四边形的四个内角之___,也就是它们的和为____.
可以
四
四
和
360
想一想
上面我们讨论的一般三角形和四边形都可以平面镶嵌,因为三角形的内角和是180°,四边形内角和是360°它们的内角和是整数倍都是360°,那么其它的一般多边形能进行镶嵌吗?
例如:在五边形中,内角和540°,已经超过360°,即每一个内角拼接在一起时有重叠部分,不符合平面镶嵌的含义。当边数越大时,内角和也越大,更不符合要求,因此边数大于4的一般多边形不可以平面镶嵌。
结论:
1.要用图形不留空隙、不重叠地镶嵌一个平面区域,需使得拼接点处的所有角之和等于360°。
2.任意形状但全等的三角形都可以进行镶嵌
3.任意形状但全等的四边形也都可以进行镶嵌
4.用一种正多边形可以进行镶嵌的是:正三角形、
正方形、正六边形
5.用两种正多边形可以进行镶嵌的是:正三角形和正方形、正三角形和正六边形、正方形和正八边形 正三角形和正十二边形等
6.用三种正多边形可以进行镶嵌的是:正三角形和正方形和正六边形、正方形和正五边形和正十二边形等
图形美
图形美
巩固练习:
1.只用下列一种正多边形不能镶嵌成平面图案的是( )
?A.正三角形 B.正方形 C.正五边形 D.正六边形
2.下列图形中,能镶嵌成平面图案的是( )
A.正六边形 B.正七边形 C.正八边形 D.正九边形
3.不能镶嵌成平面图案的正多边形组合为( )
A.正八边形和正方形 B.正五边形和正十边形
C.正六边形和正三角形 D.正六边形和正八边形
4.某学校的教室在装修过程中,准备用边长相等 的正方形和正三角形两种地砖镶嵌地面,在每个顶点周围的正方形、正三角形地砖的块数可以分别是( )
?A.2,2 B.2,3 C.1,2 D.2,1
C
A
B
B
拓展训练:
你认为图a与图b所示的两个图形哪一个能用来进行镶嵌?说出你的判断.
如果能进行镶嵌,请你用这个图形
设计一个图案.
谢 谢
19.4 综合与实践 多边形的镶嵌
19.4 综合与实践
多边形的镶嵌
上课教师:施佑新
上课时间:2019.5.28
定义: 用形状相同或不同的
平面封闭图形,覆盖平面区域,
使图形间既无缝隙又不重叠地
全部覆盖,在几何里面叫做平
面镶嵌.
探究1:仅用一种正多边形镶嵌,哪些正多边形能单独镶嵌成一个平面图案?
正方形
正三角形
正六边形
做一做:
要用正多边形镶嵌成一个平面, 关键是:这种正多边形内角的度数能整除360°。
镶嵌满足的条件:
能铺满地面的多边形,围绕某
一点的内角和为( )
思考:什么样的正多边形能够进行镶嵌
360°
啊!拼不了啦,为什么呢 你能说说道理吗
1
2
3
∠1+∠2+∠3=
用边长相同的正五边形能否镶嵌?
理一理
6
60
o
90
o
108
o
120
o
4
3
3
能拼好
能拼好
不能拼好
有缺口
能拼好
60 ×6=360
o
o
90 ×4=360
o
o
108 ×3<360
o
o
120 ×3=360
o
o
实 验 结 果
正n边形
拼图
每个内角度数
多边形个数
结果
n = 3
n = 4
n =5
n = 6
还能找到能镶嵌的其他正多边形吗?
。
k ·
(n-2)×180
n
= 360
。
(n-2)(k-2)=4
k=6
n=3
k=4
n=4
k=3
n=6
设在一个顶点周围有 k 个正 n 边形的角,则有
∵ k 为正整数, n 为大于等于 3 的正整数
∴解为
探究2:用边长相等的两种正多边形镶嵌,哪两种正多边形能镶嵌成一个平面图案?
正三角形
正方形
正六边形
60°×3+90°×2=360°
正三角形和正方形
(一)正三角形与正方形
2 m+3 n=12
m=3
n=2
m·60°+n·90° =360°
设在一个顶点周围有 m 个正三角形的角,n 个正方形的角,则有
∵ m,n 为正整数
∴解为
正三角形和正六边形
60°×4 + 120°=360°
60°×2+120°×2=360°
(二)正三角形与正六边形
m+2n=6
m=2
n=2
m=4
n=1
m·60°+n·120 °=360°
设在一个顶点周围有 m 个正三角形的角,n 个正六
边形的角,则有
∵ m,n 为正整数
∴解为
想一想
正方形和正八边形能否镶嵌
正三角形和正十二边形能否镶嵌
你能说出其中的道理吗?
135°
135°
90°
150°
150°
60°
正方形和正八边形
正三角形和正十二边形
正方形和正六边形能否镶嵌
www..cn
正方形和正六边形
用两种正多边形进行镶嵌应满足什么条件 ?
当围绕一点拼在一起的两种正多边形的内角加在一起恰好组成一个周角时,这两种正多边形就能镶嵌.
规律:
正五边形、正十边形
围绕一点能拼成360 ,但能扩展到整个平面,即铺满地面吗?
尽管能围绕一点拼成360 ,但不能扩展到整个平面.
结论:用两种正多边形进行平面镶嵌, 有以下五种可能:
(3个)正三角形+(2个)正方形
(4个)正三角形+(1个)正六边形
(2个)正三角形+(2个)正六边形
(1个)正三角形+(2个)正十二边形
(1个)正方形 + (2个)正八边形
正十二边形与正方形、正五边形的平面镶嵌
思考:用三种以上不同正多边形可以作平面
镶嵌吗?
正三角形与正方形、正六边形的平面镶嵌
探究3:
用几个形状、大小相同的任意三角形能镶嵌成一个平面图案吗?四边形呢?
1
3
2
1
4
3
2
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
(一)同一种任意三角形的镶嵌
结论:形状、大小完全相同的任意三角形能镶嵌成平面图形。
通过探究我发现:
1.任意形状、大小相同的三角形都____镶嵌,
2.在每个拼接点处有___个角,而这___个角的和恰好是这个三角形的内角和的___倍,也就是它们的和为____.
可以
六
六
两
360o
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
(二)同一种任意四角形的镶嵌
结论:形状、大小相同的任意四边形能镶嵌成平面图形。
通过探究我发现:
1.任意形状大小相同的四边形__ _镶嵌.
2.在每个拼接点处有___个角,而这___个角的和恰好是这个四边形的四个内角之___,也就是它们的和为____.
可以
四
四
和
360
想一想
上面我们讨论的一般三角形和四边形都可以平面镶嵌,因为三角形的内角和是180°,四边形内角和是360°它们的内角和是整数倍都是360°,那么其它的一般多边形能进行镶嵌吗?
例如:在五边形中,内角和540°,已经超过360°,即每一个内角拼接在一起时有重叠部分,不符合平面镶嵌的含义。当边数越大时,内角和也越大,更不符合要求,因此边数大于4的一般多边形不可以平面镶嵌。
结论:
1.要用图形不留空隙、不重叠地镶嵌一个平面区域,需使得拼接点处的所有角之和等于360°。
2.任意形状但全等的三角形都可以进行镶嵌
3.任意形状但全等的四边形也都可以进行镶嵌
4.用一种正多边形可以进行镶嵌的是:正三角形、
正方形、正六边形
5.用两种正多边形可以进行镶嵌的是:正三角形和正方形、正三角形和正六边形、正方形和正八边形 正三角形和正十二边形等
6.用三种正多边形可以进行镶嵌的是:正三角形和正方形和正六边形、正方形和正五边形和正十二边形等
图形美
图形美
巩固练习:
1.只用下列一种正多边形不能镶嵌成平面图案的是( )
?A.正三角形 B.正方形 C.正五边形 D.正六边形
2.下列图形中,能镶嵌成平面图案的是( )
A.正六边形 B.正七边形 C.正八边形 D.正九边形
3.不能镶嵌成平面图案的正多边形组合为( )
A.正八边形和正方形 B.正五边形和正十边形
C.正六边形和正三角形 D.正六边形和正八边形
4.某学校的教室在装修过程中,准备用边长相等 的正方形和正三角形两种地砖镶嵌地面,在每个顶点周围的正方形、正三角形地砖的块数可以分别是( )
?A.2,2 B.2,3 C.1,2 D.2,1
C
A
B
B
拓展训练:
你认为图a与图b所示的两个图形哪一个能用来进行镶嵌?说出你的判断.
如果能进行镶嵌,请你用这个图形
设计一个图案.
谢 谢
