沪科版七年级下册 10.3 平行线的性质课件(共14张PPT)
文档属性
| 名称 | 沪科版七年级下册 10.3 平行线的性质课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 488.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-24 22:31:22 | ||
图片预览




文档简介
(共15张PPT)
10.3平行线的性质(2)
如图,已知AG//CF,AB//CD,
∠A=40 ,求∠C的度数。
F
A
B
C
D
E
G
1
解:
∵ AG//CF(已知)
∴ ∠A=∠1
(两直线平行,同位角相等)
又∵AB//CD(已知)
∴ ∠1=∠C
(两直线平行,同位角相等)
∴ ∠A=∠C
(等量代换)
∵ ∠A=40
∴ ∠C=40
做一做
F
A
B
C
D
E
G
1
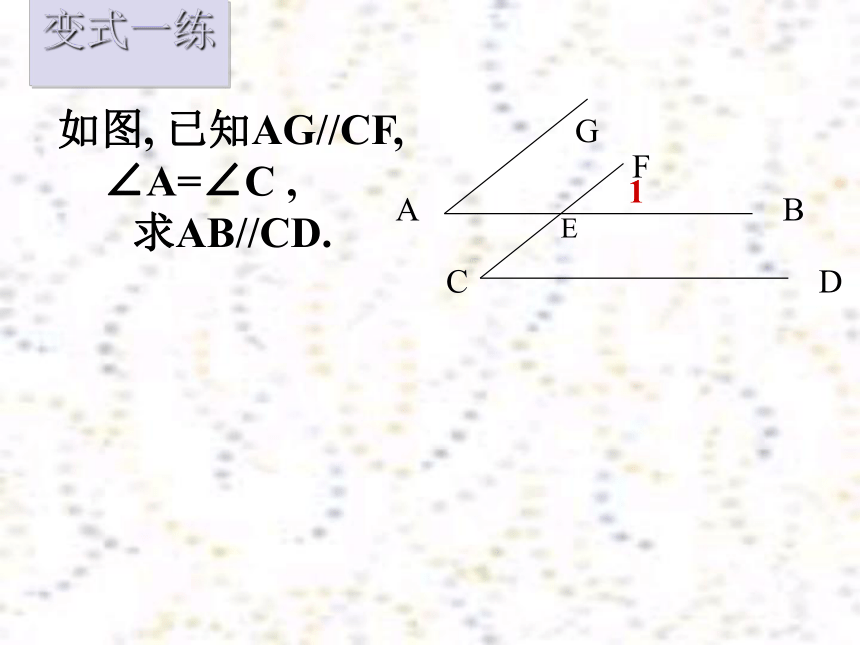
如图, 已知AG//CF,
∠A=∠C ,
求AB//CD.
变式一练
合作学习
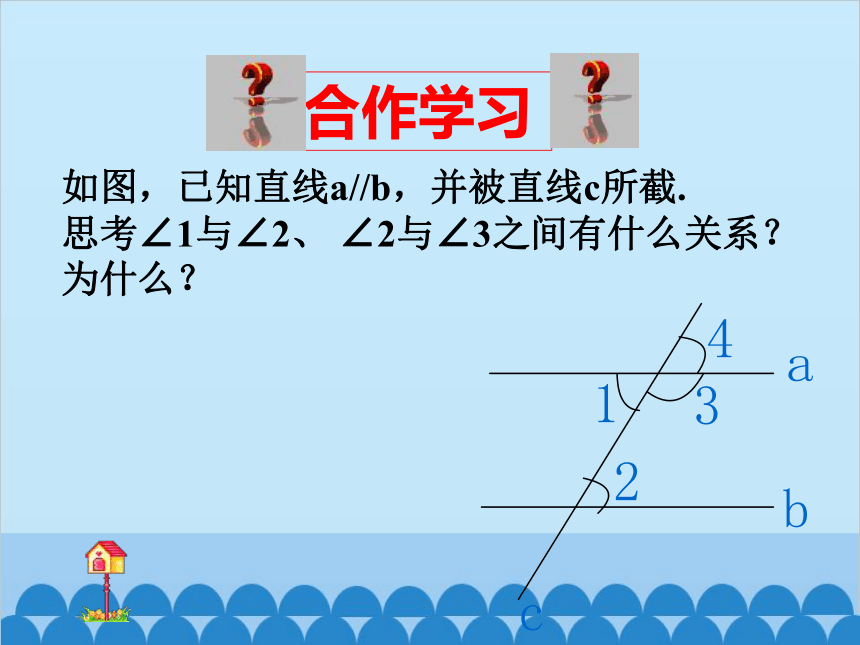
如图,已知直线a//b,并被直线c所截.
思考∠1与∠2、 ∠2与∠3之间有什么关系?
为什么?
议一议
性质
两直线平行,内错角相等.
两直线平行,同旁内角互补.
两条平行直线被第三条直线所截,
内错角相等,同旁内角互补
简记为:
判定和性质的比较
两条平行直线被第三条直线直线所截,
同位角相等, 两直线平行
两直线平行,同位角相等。
判定
性质
条件 结论
条件 结论
思考:
1、判定与性质的
条件与结论有什么关系?
互换。
内错角相等, 两直线平行
两直线平行,内错角相等。
同旁内角互补,两直线平行
两直线平行,同旁内角互补
2、使用判定时是
已知 ,说明 ;
角的相等或互补
二直线平行
使用性质时是
已知 ,说明 。
二直线平行
角的相等或互补
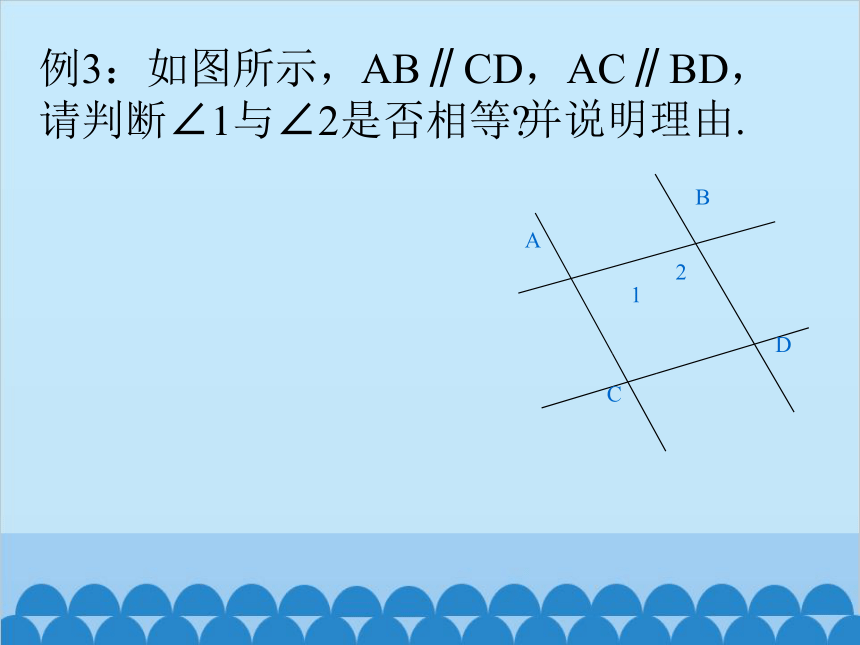
例3:如图所示,AB∥CD,AC∥BD,
请判断∠1与∠2是否相等
A
B
C
D
1
2
并说明理由.
c
d
a
b
3
4
2
1
如图所示 ∠1 =∠2
求证 : ∠3 =∠4
证明:∵ ∠1 =∠2(已知)
∴a//b
(同位角相等,两直线平行)
∴ ∠3 =∠4
(两直线平行,内错角相等)
例4:如图,已知∠ABC+∠C=1800,BD平分∠ABC,∠CBD与∠D相等吗 请说明理由.
A
D
C
B
知识巩固
(1)如图1,AB∥CD, ∠1=45°, ∠D= ∠C,依次求出∠D, ∠C, ∠B的度数.
(2)在下图所示的3个图中,a∥b,分别计算∠1的度数.
D
C
A
B
1
a
a
a
b
b
b
2
1
1
36°
120°
1
CED+ C=180 ( ).
练习二:
填空:如图(1):
AB CD (已知),
B= C ( ).
如图(2):
ADE= B (已知),
DE BC ( ),
两直线平行,内错角相等
同位角相等,两直线平行
两直线平行,同旁内角互补
(1)
(2)
A
B
C
D
E
B
A
C
D
如图所示, 已知AB//CD ,AD//BC, BF平分∠ABC ,DE平分∠ADC,
则 DE//FB,请说明理由.
D
F
C
A
E
B
能力大挑战
今天你有什么收获
蓦然回首
平行线的判定
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
平行线的性质
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
10.3平行线的性质(2)
如图,已知AG//CF,AB//CD,
∠A=40 ,求∠C的度数。
F
A
B
C
D
E
G
1
解:
∵ AG//CF(已知)
∴ ∠A=∠1
(两直线平行,同位角相等)
又∵AB//CD(已知)
∴ ∠1=∠C
(两直线平行,同位角相等)
∴ ∠A=∠C
(等量代换)
∵ ∠A=40
∴ ∠C=40
做一做
F
A
B
C
D
E
G
1
如图, 已知AG//CF,
∠A=∠C ,
求AB//CD.
变式一练
合作学习
如图,已知直线a//b,并被直线c所截.
思考∠1与∠2、 ∠2与∠3之间有什么关系?
为什么?
议一议
性质
两直线平行,内错角相等.
两直线平行,同旁内角互补.
两条平行直线被第三条直线所截,
内错角相等,同旁内角互补
简记为:
判定和性质的比较
两条平行直线被第三条直线直线所截,
同位角相等, 两直线平行
两直线平行,同位角相等。
判定
性质
条件 结论
条件 结论
思考:
1、判定与性质的
条件与结论有什么关系?
互换。
内错角相等, 两直线平行
两直线平行,内错角相等。
同旁内角互补,两直线平行
两直线平行,同旁内角互补
2、使用判定时是
已知 ,说明 ;
角的相等或互补
二直线平行
使用性质时是
已知 ,说明 。
二直线平行
角的相等或互补
例3:如图所示,AB∥CD,AC∥BD,
请判断∠1与∠2是否相等
A
B
C
D
1
2
并说明理由.
c
d
a
b
3
4
2
1
如图所示 ∠1 =∠2
求证 : ∠3 =∠4
证明:∵ ∠1 =∠2(已知)
∴a//b
(同位角相等,两直线平行)
∴ ∠3 =∠4
(两直线平行,内错角相等)
例4:如图,已知∠ABC+∠C=1800,BD平分∠ABC,∠CBD与∠D相等吗 请说明理由.
A
D
C
B
知识巩固
(1)如图1,AB∥CD, ∠1=45°, ∠D= ∠C,依次求出∠D, ∠C, ∠B的度数.
(2)在下图所示的3个图中,a∥b,分别计算∠1的度数.
D
C
A
B
1
a
a
a
b
b
b
2
1
1
36°
120°
1
CED+ C=180 ( ).
练习二:
填空:如图(1):
AB CD (已知),
B= C ( ).
如图(2):
ADE= B (已知),
DE BC ( ),
两直线平行,内错角相等
同位角相等,两直线平行
两直线平行,同旁内角互补
(1)
(2)
A
B
C
D
E
B
A
C
D
如图所示, 已知AB//CD ,AD//BC, BF平分∠ABC ,DE平分∠ADC,
则 DE//FB,请说明理由.
D
F
C
A
E
B
能力大挑战
今天你有什么收获
蓦然回首
平行线的判定
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
平行线的性质
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
