物理人教版(2019)必修第二册8.2重力势能(共41张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册8.2重力势能(共41张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-24 22:25:20 | ||
图片预览









文档简介
(共41张PPT)
人教版 必修第二册
8.2 重力势能
第八章 机械能守恒定律
一个拇指大的小石块,
在4楼抛下时可能伤人头皮,
而在25楼抛下时可能会让路人当场送命。
一个4厘米的铁钉在18楼甩下时,
可能会造成行人的致命伤害。
在重力加速度的作用下,
一颗鸡蛋都可能成为致命杀手。
当达到一定的高度,
即便很轻的物体,
也会造成很大的伤害。
一个50克的鸡蛋
从4楼抛下来就会让人起肿包
从8楼抛下来就会让人头皮破裂
从18楼高甩下来就可以砸破行人的头骨
从25楼抛下可使人当场死亡
引入新课
引入新课
这是因为物体一旦处在一定高度时,就具有了一定的能量。而当它从所处的的高处落下时,这些能量就会以做功的方式释放出来。
初中我们已经定性地学习了重力势能,物体的质量越大、所处的位置越高,重力势能就越大。这一节我们来进一步定量地研究重力势能。你认为重力势能的表达式应该是怎样的呢?
问题
一、重力做的功
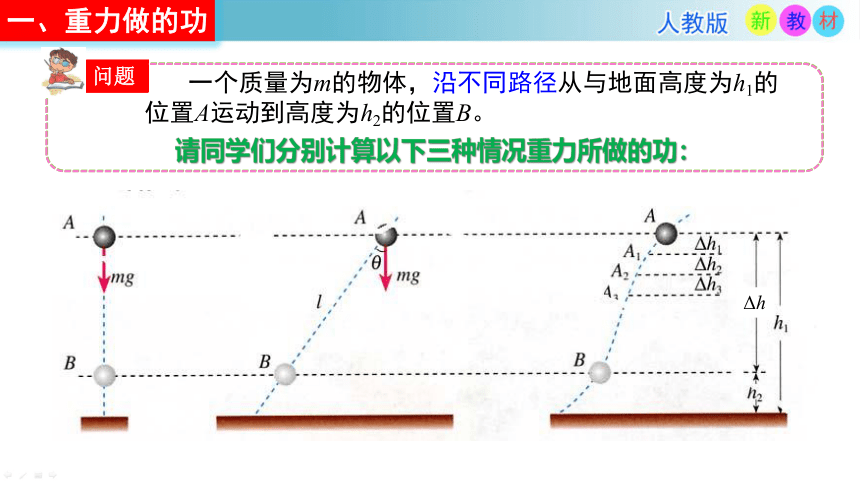
一个质量为m的物体,沿不同路径从与地面高度为h1的位置A运动到高度为h2的位置B。
请同学们分别计算以下三种情况重力所做的功:
问题
问题
问题
Δh
一、重力做的功
WG=mgΔh
=mg(h1-h2)
(1)一个质量为m的物体,从与地面高度为h1的位置A,竖直向下运动到高度为h2的位置B (如图),这个过程中重力做的功是多少?
=mgh1-mgh2
一、重力做的功
=mgh1-mgh2
WG1=mglcosθ
=mgΔh
(2)质量为m的物体从高度为h1的A点沿直线斜面运动到高度为h2的B′点(如图),这个过程中重力做的功是多少?
Δh
=mg(h1-h2)
一、重力做的功
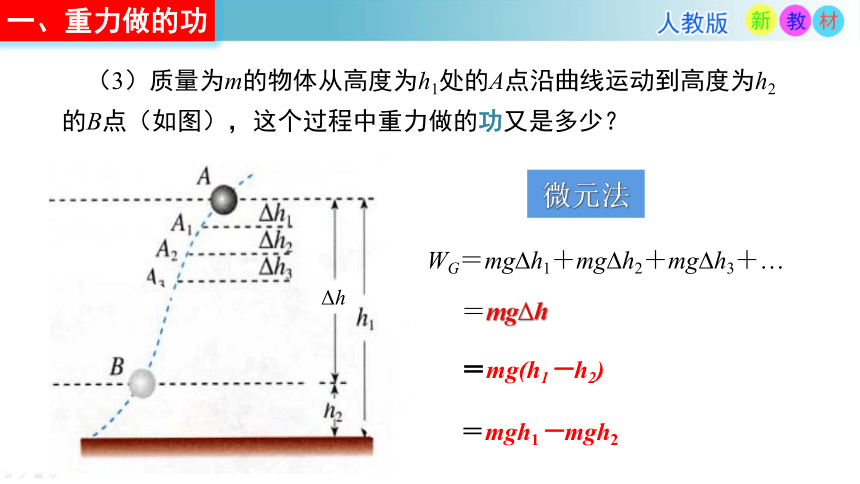
微元法
WG=mg h1+mg h2+mg h3+…
=mgΔh
(3)质量为m的物体从高度为h1处的A点沿曲线运动到高度为h2的B点(如图),这个过程中重力做的功又是多少?
Δh
=mgh1-mgh2
=mg(h1-h2)
一、重力做的功
WG = mgΔh
= mgh1-mgh2
WG = mgLcos θ
= mgΔh
= mgh1-mgh2
WG = mg h1+mg h2+mg h3+…
= mgΔh
= mgh1-mgh2
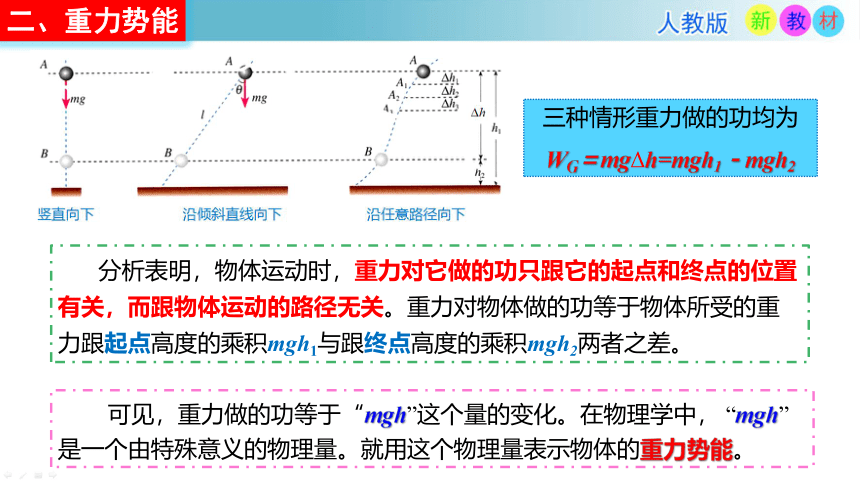
竖直向下
沿倾斜直线向下
沿任意路径向下
Δh
一、重力做的功
重力做功的特点:
物体运动时,重力对它做的功只跟它的起点和终点的位置有关,而跟物体运动的路径无关。
板书设计
一、重力做的功
1、重力做的功WG=mgΔh,Δh指初位置与末位置的高度差。
2、重力做功的特点:物体运动时,重力对它做的功只跟它的起点和终点的位置有关,而跟物体运动的路径无关。
二、重力势能
三种情形重力做的功均为
WG=mgΔh=mgh1-mgh2
分析表明,物体运动时,重力对它做的功只跟它的起点和终点的位置有关,而跟物体运动的路径无关。重力对物体做的功等于物体所受的重力跟起点高度的乘积mgh1与跟终点高度的乘积mgh2两者之差。
可见,重力做的功等于“mgh”这个量的变化。在物理学中, “mgh”是一个由特殊意义的物理量。就用这个物理量表示物体的重力势能。
板书设计
1、定义:物体由于被举高而具有的能量叫重力势能。
2、大小:物体的重力势能等于它所受重力与所处高度的乘积。
4、单位:焦(耳) 符号:J
Ep= mgh
二、重力势能
3、表达式:
二、重力势能
推导:WG =mgh1-mgh2
=-(mgh2-mgh1)
=-(EP2-EP1)
=-ΔEP
重力做功等于重力势能的变化量(增加量)的负值;重力做功等于重力势能的减少量。
重力做功与重力势能的关系
即
WG =-ΔEP
二、重力势能
重力做功与重力势能的关系
5、重力做功与重力势能的关系:
(1)重力对物体做的功等于重力势能变化量(增加量)的负值;
板书设计
(2)表达式:WG =mgh1-mgh2 =-(mgh2-mgh1)
=-(EP2-EP1)
=-ΔEP
重力做功WG (正、负) 重力势能EP (增加、减少) 重力做功和重力势能变化的关系
物体上升
物体下降
正
负
减少
增加
重力做的功等于重力势能的减少
物体克服重力做的功等于重力势能的增加
(3)重力做正功和负功的意义
即
WG =-ΔEP
例1. 塔吊把一质量为 200 kg 的物体,从距地面高为 h1 = 8 m的高度匀速运到高为 h2 = 3 m 的地方,重力做了多少功?物体的重力势能如何变化?
重力势能减少了 10000 J
结论1:物体下降,重力做正功,重力势能减少;重力势能减少的数量等于重力做的功。
二、重力势能
重力做的功:WG =mgΔh=mg(h1-h2)
=200×10×(8-3) J=10000 J
例2. 塔吊把一质量为 200 kg 的物体,从距地面高为 h1 = 3 m的高度匀速运到高为 h2 = 8 m 的地方,重力做了多少功?物体克服重力做了多少功?物体的重力势能如何变化?
物体克服重力做了 10000 J
重力势能增加了 10000 J
结论2:物体上升,重力做负功,重力势能增加,重力势能增加的数量等于物体克服重力所做的功。
二、重力势能
重力做的功:WG =mgΔh=mg(h1-h2)
=200×10×(3-8) J=-10000 J
(1)当物体由高处向低处运动时:重力做正功,即WG>0,EP初>EP末 ,重力势能减少,且减少的重力势能等于重力做的正功。
(2)当物体由低处向高处运动时:重力做负功,即WG<0,EP初<EP末 ,重力势能增加,且增加的重力势能等于物体克服重力所做的功。
小结
板书设计
二、重力势能
重力势能的相对性
高度h是相对于谁的呢?
重力势能总是相对于某个水平面来说的,这个水平面叫参考平面.
Ep= mgh
8848.86
(1)物体在参考面上,h=0,Ep=0,
(2)物体在参考面上方,h为正值,Ep为正值;
参考面即高度为零的平面,一般来说参考面可以任意选取
参考面又称零势能面;
正负表示大小
(h是物体相对参考面的高度)
(3)物体在参考面下方,h为负值,Ep为负值。
二、重力势能
重力势能的相对性
Ep= mgh
EP( J )
EP( J )
EP( J )
地面
桌面
天花板
参考平面
0
0
0
mgh2
mg(h1+h2)
-mgh2
mgh1
-mgh1
-mg(h1+h2)
h1
h2
A
B
C
天花板
桌面
地面
二、重力势能
重力势能的相对性
那么重力势能是谁具有的呢
物体重力势能与重力做功密切相关,而重力是地球与物体间的相互作用力,若离开了地球或物体,就谈不上重力,所以,重力势能是物体与地球所组成的“系统”所共有的。平常只说物体具有的重力势能,是一种简化的说法。
二、重力势能
重力势能的系统性
(1)参考平面:
①选定某一个水平面,并把这个水平面的高度定为零,则物体在该平面上的重力势能为零(又称零势能面)。
②由于高度h是相对的,所以重力势能也是相对的,计算重力势能之前需要先选定0势能参考平面。;
③参考平面的选取是任意的,通常选择地面为参考平面。
(2)重力势能是标量,但有正负,且正负表示大小。
①若物体在参考面,h=0,故Ep=0;
②若物体在参考面上方,则h>0为正值,Ep也是正值;
③若物体在参考面下方,则h<0为负值,Ep也是负值。
6、重力势能的相对性:
板书设计
7、重力势能的“四性”
板书设计
(1)标量性
①重力势能是标量,只有大小,没有方向,但有正负。
②重力势能正负的含义:正负值分别表示物体处于参考平面上方和下方。
(2)相对性
选取不同的水平面作为参考平面,其重力势能具有不同的数值,即重力势能的大小与参考平面的选取有关。
(3)绝对性
物体在两个高度不同的位置时,由于高度差一定,重力势能之差也是一定的,即物体的重力势能的变化与参考平面的选取无关。
(4)系统性
重力势能是物体与地球所组成的“系统”所共有的。
三、弹性势能
拉开的弓
拉长的弹簧
弯曲的撑杆
压缩的弹簧
三、弹性势能
拉长或压缩的弹簧、卷紧的发条、拉开的弓、正在击球的网球拍、撑竿跳高运动员手中弯曲的竿等等,这些物体都发生了弹性形变,每个物体的各部分之间都有弹力的相互作用。发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫作弹性势能。
三、弹性势能
(2)与劲度系数有关:不同的弹簧发生同样大小的形变,劲度系数越大,弹性势能越大。
物体的弹性势能跟哪些因素有关?
(1)与形变量的大小有关:对于同一根弹簧,形变量越大,弹性势能越大。
总结:弹性势能与劲度系数和形变量有关。劲度系数越大,形变量越大,弹性势能越大。
三、弹性势能
疑惑:求拉力做功能否直接用W=Flcosα?
这是一个变力做功问题,不能直接用功的公式计算。
F
l
思考:弹簧在拉力F的作用下移动了l (在弹性限度内),求拉力做的功。
如何计算弹力做的功?
三、弹性势能
因拉力F与形变量l成正比,故拉力的平均值为 :
平均拉力对这段位移做的功:
F拉
l
F = k l
如何计算弹力做的功?
WF弹=-WF拉
弹力做的功:
重力做正功,重力势能减小;
重力做负功,重力势能增加。
弹力做正功,弹性势能减少;
弹力做负功,弹性势能增加。
重力做功
重力势能的变化
弹性势能的变化
弹力做功
回顾:
类比思想
弹簧的弹性势能与弹力做功的关系
三、弹性势能
三、弹性势能
WF弹=EP1-EP2= -△ EP
弹力做的功
初状态的弹性势能
末状态的弹性势能
弹力做功与弹性势能的关系:弹力做的功等于弹性势能变化量的负值。
弹簧的弹性势能与弹力做功的关系
WG=EP1-EP2= -△ EP
重力做的功
初状态的重力势能
末状态的重力势能
类比思想
三、弹性势能
可见弹簧的弹性势能表达式为:
l为弹簧的形变量
k为弹簧的劲度系数
WF弹=-WF拉=EP1-EP2
l
F拉
F弹
WF拉= k l 2
1
2
EP1=0 ,
弹性势能的表达式
重力势能是由地球和地面上物体的相对位置决定的。
弹性势能是由发生弹性形变的物体各部分的相对位置决定的。
三、弹性势能
势能也叫位能
势能也叫位能,与相互作用的物体的相对位置有关。
板书设计
1、定义:发生弹性形变的物体各部分之间由于弹力的相互作用而具有的势能,叫做弹性势能。
3、影响弹性势能的因素:
三、弹性势能
2、表达式:
(x为弹簧的形变量, k为弹簧的劲度系数)
(1)弹簧的形变量x;
(2)弹簧的劲度系数。
4、对弹性势能的理解:
(1)一般规定弹簧在原长时,弹簧的弹性势能为零,故没有负值;
(2)系统性:弹性势能是发生弹性形变的物体上所有质点因相对位置改变而具有的能量,因此弹性势能具有系统性。
(3)相对性:弹性势能的大小与选定的零势能位置有关,对于弹簧,一般规定弹簧处于原长时的势能为零势能。
板书设计
5、弹力做功与弹性势能的关系:
(1)弹力做正功时,弹性势能减少。
(2)弹力做负功时,弹性势能增加。
(3)弹力做功与弹性势能变化的关系:弹力做的功等于弹性势能变化量(增加量)的负值;即 W弹=-ΔEp.
6、位能:势能也叫位能,与相互作用的物体的相对位置有关。重力势能是由地球和地面上物体的相对位置决定的,弹性势能是由发生弹性形变的物体各部分的相对位置决定的。
【典例1】(2021·全国高一课时练习)如图所示,射箭时人通过拉弓引起弹性势能的增加,此时的弹性势能主要( )
A.存储在箭上
B.存储在弓上
C.存储在弦上
D.存储于拉弓人的手上
【正确答案】B
随堂练习
【典例2】(多选)关于弹性势能,下列说法中正确的是( )
A.任何发生弹性形变的物体都具有弹性势能
B.任何具有弹性势能的物体,都一定发生了弹性形变
C.物体只要发生形变就一定有弹性势能
D.弹簧的弹性势能只跟弹簧的形变量有关
【正确答案】AB
随堂练习
【典例3】下面有关重力势能的说法中,正确的是( )
A. 举得越高的物体,具有的重力势能越大
B. 质量越大的物体,具有重力势能越大
C. 物体的重力势能不可能为零
D. 物体的重力势能可能小于零
D
随堂练习
【典例4】 以下叙述中正确的是( )
A. 重力对物体做功越多,物体的重力势能越少
B. 物体克服重力做功越多,物体的重力势能越少
C. 重力对物体不做功,物体的重力势能一定为零
D. 物体没克服重力做功,物体的重力势能不一定为零
D
随堂练习
【典例5】下列关于重力势能的说法,正确的是 ( )
A. 重力势能的变化,只跟物体所处的初末位置有关,与物体实际经过的路径无关
B. 重力势能的变化,只跟重力做功有关,和其他力做功多少无关
C. 重力势能是矢量,当重力对物体做正功时,物体的重力势能减少
D. 重力势能是物体和地球共有的,而不是物体单独具有的
ABD
随堂练习
【典例6】一质量为 5 kg 的小球从 5 m 高处下落,碰撞地面后弹起,每次弹起的高度比下落的高度低 1 m ,则小球从下落到停在地面的过程中重力一共做了多少功?重力势能如何变化,变化多少?( g = 10m/s2 )
解: 小球下落高度为 5 m,则重力做功为
WG = mgh = 5 kg×10 m/s2×5 m = 250 J
小球下落过程中重力做正功,重力势能减少,
减少的重力势能等于重力做的功,为 250 J。
随堂练习
谢谢!
人教版 必修第二册
8.2 重力势能
第八章 机械能守恒定律
一个拇指大的小石块,
在4楼抛下时可能伤人头皮,
而在25楼抛下时可能会让路人当场送命。
一个4厘米的铁钉在18楼甩下时,
可能会造成行人的致命伤害。
在重力加速度的作用下,
一颗鸡蛋都可能成为致命杀手。
当达到一定的高度,
即便很轻的物体,
也会造成很大的伤害。
一个50克的鸡蛋
从4楼抛下来就会让人起肿包
从8楼抛下来就会让人头皮破裂
从18楼高甩下来就可以砸破行人的头骨
从25楼抛下可使人当场死亡
引入新课
引入新课
这是因为物体一旦处在一定高度时,就具有了一定的能量。而当它从所处的的高处落下时,这些能量就会以做功的方式释放出来。
初中我们已经定性地学习了重力势能,物体的质量越大、所处的位置越高,重力势能就越大。这一节我们来进一步定量地研究重力势能。你认为重力势能的表达式应该是怎样的呢?
问题
一、重力做的功
一个质量为m的物体,沿不同路径从与地面高度为h1的位置A运动到高度为h2的位置B。
请同学们分别计算以下三种情况重力所做的功:
问题
问题
问题
Δh
一、重力做的功
WG=mgΔh
=mg(h1-h2)
(1)一个质量为m的物体,从与地面高度为h1的位置A,竖直向下运动到高度为h2的位置B (如图),这个过程中重力做的功是多少?
=mgh1-mgh2
一、重力做的功
=mgh1-mgh2
WG1=mglcosθ
=mgΔh
(2)质量为m的物体从高度为h1的A点沿直线斜面运动到高度为h2的B′点(如图),这个过程中重力做的功是多少?
Δh
=mg(h1-h2)
一、重力做的功
微元法
WG=mg h1+mg h2+mg h3+…
=mgΔh
(3)质量为m的物体从高度为h1处的A点沿曲线运动到高度为h2的B点(如图),这个过程中重力做的功又是多少?
Δh
=mgh1-mgh2
=mg(h1-h2)
一、重力做的功
WG = mgΔh
= mgh1-mgh2
WG = mgLcos θ
= mgΔh
= mgh1-mgh2
WG = mg h1+mg h2+mg h3+…
= mgΔh
= mgh1-mgh2
竖直向下
沿倾斜直线向下
沿任意路径向下
Δh
一、重力做的功
重力做功的特点:
物体运动时,重力对它做的功只跟它的起点和终点的位置有关,而跟物体运动的路径无关。
板书设计
一、重力做的功
1、重力做的功WG=mgΔh,Δh指初位置与末位置的高度差。
2、重力做功的特点:物体运动时,重力对它做的功只跟它的起点和终点的位置有关,而跟物体运动的路径无关。
二、重力势能
三种情形重力做的功均为
WG=mgΔh=mgh1-mgh2
分析表明,物体运动时,重力对它做的功只跟它的起点和终点的位置有关,而跟物体运动的路径无关。重力对物体做的功等于物体所受的重力跟起点高度的乘积mgh1与跟终点高度的乘积mgh2两者之差。
可见,重力做的功等于“mgh”这个量的变化。在物理学中, “mgh”是一个由特殊意义的物理量。就用这个物理量表示物体的重力势能。
板书设计
1、定义:物体由于被举高而具有的能量叫重力势能。
2、大小:物体的重力势能等于它所受重力与所处高度的乘积。
4、单位:焦(耳) 符号:J
Ep= mgh
二、重力势能
3、表达式:
二、重力势能
推导:WG =mgh1-mgh2
=-(mgh2-mgh1)
=-(EP2-EP1)
=-ΔEP
重力做功等于重力势能的变化量(增加量)的负值;重力做功等于重力势能的减少量。
重力做功与重力势能的关系
即
WG =-ΔEP
二、重力势能
重力做功与重力势能的关系
5、重力做功与重力势能的关系:
(1)重力对物体做的功等于重力势能变化量(增加量)的负值;
板书设计
(2)表达式:WG =mgh1-mgh2 =-(mgh2-mgh1)
=-(EP2-EP1)
=-ΔEP
重力做功WG (正、负) 重力势能EP (增加、减少) 重力做功和重力势能变化的关系
物体上升
物体下降
正
负
减少
增加
重力做的功等于重力势能的减少
物体克服重力做的功等于重力势能的增加
(3)重力做正功和负功的意义
即
WG =-ΔEP
例1. 塔吊把一质量为 200 kg 的物体,从距地面高为 h1 = 8 m的高度匀速运到高为 h2 = 3 m 的地方,重力做了多少功?物体的重力势能如何变化?
重力势能减少了 10000 J
结论1:物体下降,重力做正功,重力势能减少;重力势能减少的数量等于重力做的功。
二、重力势能
重力做的功:WG =mgΔh=mg(h1-h2)
=200×10×(8-3) J=10000 J
例2. 塔吊把一质量为 200 kg 的物体,从距地面高为 h1 = 3 m的高度匀速运到高为 h2 = 8 m 的地方,重力做了多少功?物体克服重力做了多少功?物体的重力势能如何变化?
物体克服重力做了 10000 J
重力势能增加了 10000 J
结论2:物体上升,重力做负功,重力势能增加,重力势能增加的数量等于物体克服重力所做的功。
二、重力势能
重力做的功:WG =mgΔh=mg(h1-h2)
=200×10×(3-8) J=-10000 J
(1)当物体由高处向低处运动时:重力做正功,即WG>0,EP初>EP末 ,重力势能减少,且减少的重力势能等于重力做的正功。
(2)当物体由低处向高处运动时:重力做负功,即WG<0,EP初<EP末 ,重力势能增加,且增加的重力势能等于物体克服重力所做的功。
小结
板书设计
二、重力势能
重力势能的相对性
高度h是相对于谁的呢?
重力势能总是相对于某个水平面来说的,这个水平面叫参考平面.
Ep= mgh
8848.86
(1)物体在参考面上,h=0,Ep=0,
(2)物体在参考面上方,h为正值,Ep为正值;
参考面即高度为零的平面,一般来说参考面可以任意选取
参考面又称零势能面;
正负表示大小
(h是物体相对参考面的高度)
(3)物体在参考面下方,h为负值,Ep为负值。
二、重力势能
重力势能的相对性
Ep= mgh
EP( J )
EP( J )
EP( J )
地面
桌面
天花板
参考平面
0
0
0
mgh2
mg(h1+h2)
-mgh2
mgh1
-mgh1
-mg(h1+h2)
h1
h2
A
B
C
天花板
桌面
地面
二、重力势能
重力势能的相对性
那么重力势能是谁具有的呢
物体重力势能与重力做功密切相关,而重力是地球与物体间的相互作用力,若离开了地球或物体,就谈不上重力,所以,重力势能是物体与地球所组成的“系统”所共有的。平常只说物体具有的重力势能,是一种简化的说法。
二、重力势能
重力势能的系统性
(1)参考平面:
①选定某一个水平面,并把这个水平面的高度定为零,则物体在该平面上的重力势能为零(又称零势能面)。
②由于高度h是相对的,所以重力势能也是相对的,计算重力势能之前需要先选定0势能参考平面。;
③参考平面的选取是任意的,通常选择地面为参考平面。
(2)重力势能是标量,但有正负,且正负表示大小。
①若物体在参考面,h=0,故Ep=0;
②若物体在参考面上方,则h>0为正值,Ep也是正值;
③若物体在参考面下方,则h<0为负值,Ep也是负值。
6、重力势能的相对性:
板书设计
7、重力势能的“四性”
板书设计
(1)标量性
①重力势能是标量,只有大小,没有方向,但有正负。
②重力势能正负的含义:正负值分别表示物体处于参考平面上方和下方。
(2)相对性
选取不同的水平面作为参考平面,其重力势能具有不同的数值,即重力势能的大小与参考平面的选取有关。
(3)绝对性
物体在两个高度不同的位置时,由于高度差一定,重力势能之差也是一定的,即物体的重力势能的变化与参考平面的选取无关。
(4)系统性
重力势能是物体与地球所组成的“系统”所共有的。
三、弹性势能
拉开的弓
拉长的弹簧
弯曲的撑杆
压缩的弹簧
三、弹性势能
拉长或压缩的弹簧、卷紧的发条、拉开的弓、正在击球的网球拍、撑竿跳高运动员手中弯曲的竿等等,这些物体都发生了弹性形变,每个物体的各部分之间都有弹力的相互作用。发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫作弹性势能。
三、弹性势能
(2)与劲度系数有关:不同的弹簧发生同样大小的形变,劲度系数越大,弹性势能越大。
物体的弹性势能跟哪些因素有关?
(1)与形变量的大小有关:对于同一根弹簧,形变量越大,弹性势能越大。
总结:弹性势能与劲度系数和形变量有关。劲度系数越大,形变量越大,弹性势能越大。
三、弹性势能
疑惑:求拉力做功能否直接用W=Flcosα?
这是一个变力做功问题,不能直接用功的公式计算。
F
l
思考:弹簧在拉力F的作用下移动了l (在弹性限度内),求拉力做的功。
如何计算弹力做的功?
三、弹性势能
因拉力F与形变量l成正比,故拉力的平均值为 :
平均拉力对这段位移做的功:
F拉
l
F = k l
如何计算弹力做的功?
WF弹=-WF拉
弹力做的功:
重力做正功,重力势能减小;
重力做负功,重力势能增加。
弹力做正功,弹性势能减少;
弹力做负功,弹性势能增加。
重力做功
重力势能的变化
弹性势能的变化
弹力做功
回顾:
类比思想
弹簧的弹性势能与弹力做功的关系
三、弹性势能
三、弹性势能
WF弹=EP1-EP2= -△ EP
弹力做的功
初状态的弹性势能
末状态的弹性势能
弹力做功与弹性势能的关系:弹力做的功等于弹性势能变化量的负值。
弹簧的弹性势能与弹力做功的关系
WG=EP1-EP2= -△ EP
重力做的功
初状态的重力势能
末状态的重力势能
类比思想
三、弹性势能
可见弹簧的弹性势能表达式为:
l为弹簧的形变量
k为弹簧的劲度系数
WF弹=-WF拉=EP1-EP2
l
F拉
F弹
WF拉= k l 2
1
2
EP1=0 ,
弹性势能的表达式
重力势能是由地球和地面上物体的相对位置决定的。
弹性势能是由发生弹性形变的物体各部分的相对位置决定的。
三、弹性势能
势能也叫位能
势能也叫位能,与相互作用的物体的相对位置有关。
板书设计
1、定义:发生弹性形变的物体各部分之间由于弹力的相互作用而具有的势能,叫做弹性势能。
3、影响弹性势能的因素:
三、弹性势能
2、表达式:
(x为弹簧的形变量, k为弹簧的劲度系数)
(1)弹簧的形变量x;
(2)弹簧的劲度系数。
4、对弹性势能的理解:
(1)一般规定弹簧在原长时,弹簧的弹性势能为零,故没有负值;
(2)系统性:弹性势能是发生弹性形变的物体上所有质点因相对位置改变而具有的能量,因此弹性势能具有系统性。
(3)相对性:弹性势能的大小与选定的零势能位置有关,对于弹簧,一般规定弹簧处于原长时的势能为零势能。
板书设计
5、弹力做功与弹性势能的关系:
(1)弹力做正功时,弹性势能减少。
(2)弹力做负功时,弹性势能增加。
(3)弹力做功与弹性势能变化的关系:弹力做的功等于弹性势能变化量(增加量)的负值;即 W弹=-ΔEp.
6、位能:势能也叫位能,与相互作用的物体的相对位置有关。重力势能是由地球和地面上物体的相对位置决定的,弹性势能是由发生弹性形变的物体各部分的相对位置决定的。
【典例1】(2021·全国高一课时练习)如图所示,射箭时人通过拉弓引起弹性势能的增加,此时的弹性势能主要( )
A.存储在箭上
B.存储在弓上
C.存储在弦上
D.存储于拉弓人的手上
【正确答案】B
随堂练习
【典例2】(多选)关于弹性势能,下列说法中正确的是( )
A.任何发生弹性形变的物体都具有弹性势能
B.任何具有弹性势能的物体,都一定发生了弹性形变
C.物体只要发生形变就一定有弹性势能
D.弹簧的弹性势能只跟弹簧的形变量有关
【正确答案】AB
随堂练习
【典例3】下面有关重力势能的说法中,正确的是( )
A. 举得越高的物体,具有的重力势能越大
B. 质量越大的物体,具有重力势能越大
C. 物体的重力势能不可能为零
D. 物体的重力势能可能小于零
D
随堂练习
【典例4】 以下叙述中正确的是( )
A. 重力对物体做功越多,物体的重力势能越少
B. 物体克服重力做功越多,物体的重力势能越少
C. 重力对物体不做功,物体的重力势能一定为零
D. 物体没克服重力做功,物体的重力势能不一定为零
D
随堂练习
【典例5】下列关于重力势能的说法,正确的是 ( )
A. 重力势能的变化,只跟物体所处的初末位置有关,与物体实际经过的路径无关
B. 重力势能的变化,只跟重力做功有关,和其他力做功多少无关
C. 重力势能是矢量,当重力对物体做正功时,物体的重力势能减少
D. 重力势能是物体和地球共有的,而不是物体单独具有的
ABD
随堂练习
【典例6】一质量为 5 kg 的小球从 5 m 高处下落,碰撞地面后弹起,每次弹起的高度比下落的高度低 1 m ,则小球从下落到停在地面的过程中重力一共做了多少功?重力势能如何变化,变化多少?( g = 10m/s2 )
解: 小球下落高度为 5 m,则重力做功为
WG = mgh = 5 kg×10 m/s2×5 m = 250 J
小球下落过程中重力做正功,重力势能减少,
减少的重力势能等于重力做的功,为 250 J。
随堂练习
谢谢!
