沪科版八年级下册 19.3 正方形课件(共18张PPT)
文档属性
| 名称 | 沪科版八年级下册 19.3 正方形课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 599.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-24 23:13:40 | ||
图片预览





文档简介
(共18张PPT)
正方形
19.3
*
一、教学目的
1.掌握正方形的概念、性质和判定,并会用它们进行有关的论证和计算.
2.理解正方形与平行四边形、矩形、菱形的联系和区别,提高学生的逻辑思维能力.
二、重点、难点
1.教学重点:正方形的定义及正方形与平行四边形、矩形、菱形的联系.
2.教学难点:正方形与矩形、菱形的关系及正方形性质与判定的灵活运用
*
正方形 自我介绍
在四边形的大家庭中,我有四个兄弟,
老大是平行四边形,它性格温和,
老二是菱形,它活泼可爱,
老三是矩形,他稳重大方,江湖上人称长方形,
我就是正方形老四,我集三位大哥的优点于一身,人见人爱。
*
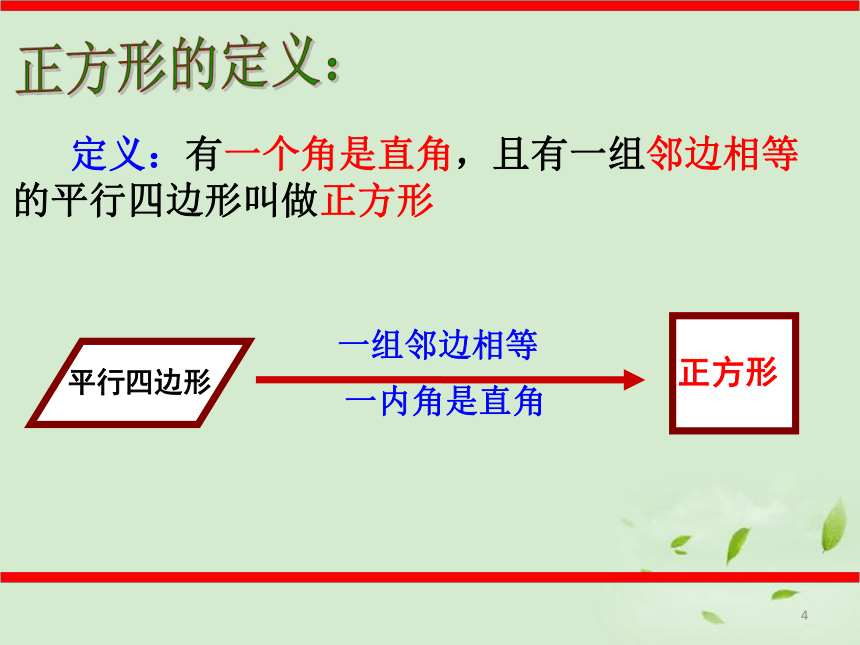
平行四边形
正方形
一组邻边相等
一内角是直角
定义:有一个角是直角,且有一组邻边相等的平行四边形叫做正方形
*
对角线: 对角线相等且互相垂直平分,每条对角线平 分一组对角。
边: 对边平行,四边相等
角 :四个角都是直角
*
正方形的性质
=菱形的性质
+矩形的性质
老师:你觉得判断一个四边形是正方形有哪些方法?
*
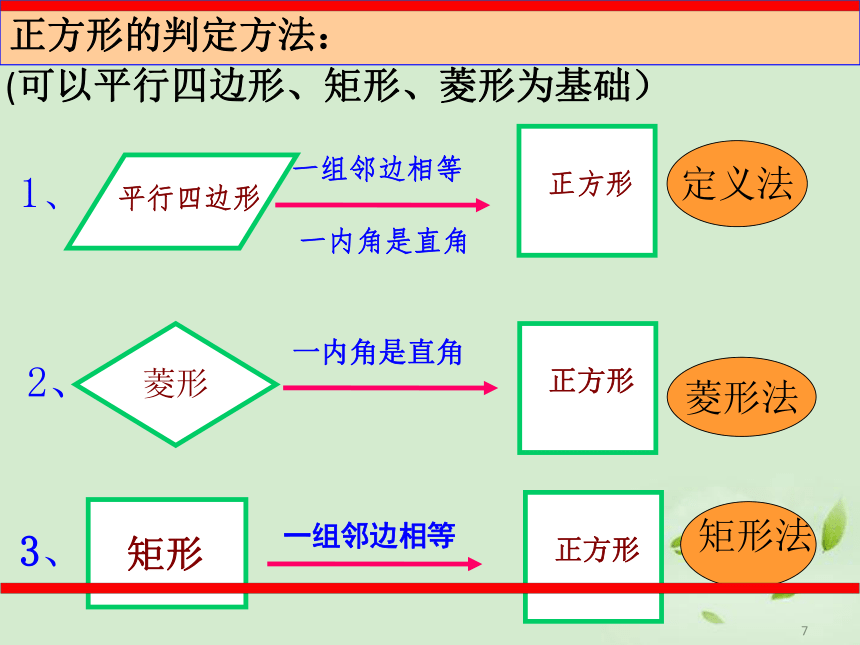
平行四边形
正方形
一组邻边相等
一内角是直角
1、
正方形
菱形
2、
一内角是直角
矩形
3、
一组邻边相等
正方形
正方形的判定方法:
(可以平行四边形、矩形、菱形为基础)
定义法
菱形法
矩形法
*
√
√
√
×
(1)正方形的一条对角线把正方形分成两个全等的
等腰直角三角形( )
(2)对角线互相垂直且相等的四边形是正方形( )
(3)如果一个菱形的对角线相等,那么它一定
是正方形 ( )
(4)如果一个矩形的对角线互相垂直,那么它
一定是正方形 ( )
(5)四条边相等且有一个角是直角的四边形是正方形( )
√
仔细思考,判一判:
(6)四个角都相等的四边形是正方形 ( )
×
*
正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直平分.
C、对角互补.
D、对角线相等.
2.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等.
B
D
火眼金睛,选一选:
*
3.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正 方形的是:( ) A.AO=BO=CO=DO,AC⊥BD
B.AD∥BC ∠A=∠C
C.AO=CO BO=DO AB=BC
D.AC=BD
A
4 .四个内角都相等,四条边也都相等的四边形一定是:( )
A.正方形 B.菱形 C.矩形 D.平行四边形
A
*
1).已知:正方形ABCD对角线AC、BD相 交于点O,且AB=2cm,则AC= ,
正方形的面积S=______.
2
2
4
6
36
2).已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,
面积S=________.则边长AB=______,
例1:填空
*
1、如图,在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB (2) BH⊥AF
牛刀小试:
*
F
A
E
G
C
B
D
H
3
A
2
1
⌒
⌒
⌒
2、如图,△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。 求证:∠CEA=∠ABG
证明:∵四边形ABDE和四边形ACFG是正方形。 ∴AE=AB AG=AC ∠1=∠2=90° 又∵∠EAC=∠1+∠BAC=90°+∠BAC ∠BAG=∠2+∠BAC=90°+∠BAC ∴∠EAC=∠BAG ∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG
*
A
B
C
D
E
F
G
N
1
2
A
B
D
C
F
E
3、如图,在正方形ABCD中,E在BC的延长线上,且CE=AC,AE交CD于F,则求∠AFC的度数。
*
例2、 直角三角形ABC中,CD平分∠ACB交AB于D,DE⊥AC,DF⊥AB。求证:四边形CEDF是正方形。
A
B
C
D
E
F
∴四边形CEDF是正方形
( )
∴ DE=DF( )
DE⊥AC, DF⊥BC
∵ CD平分∠ACB
∴ 四边形ABCD为矩形
( )
而∠ACB=90°
∴ ∠DEC=90°, ∠DFC=90°
证明:∵ DE⊥AC,DF⊥AB
有三个角是直角的四边形是矩形
角平分线的定理
有一组邻边相等的矩形是正方形
*
*
如图,点A′B′C′D′分别是正方形ABCD四条边上的点,并且AA′=BB′=CC′=DD′.
求证:四边形A′B′C′D′是正方形。
D
C
A
B
D ′
A ′
C ′
B ′
3
2
1
证明:因为四边形ABCD是正方形,所以 AB=BC=CD=DA
∵ AA′=BB′=CC′=DD′.
∴ AD′=BA′=CB′=DC′.
∵ ∠A=∠B=∠C=∠D=90°
∴ △AA′D′≌△BB′A′≌△B′CC′≌△C′DD′.
∴B′A′=C′B′=D′C′=A′D′
∴ 四边形A′B′C′D′是菱形
又 ∵ ∠1= ∠3,
∠1+ ∠2=90°
∴ ∠3+ ∠2=90°
∴ 四边形A′B′C′D′是正方形
*
∴ ∠D′A′B′=90°
练一练:
课 堂 小 结
正方形的特征:
1、正方形是特殊的平行四边形,具备平行四边形的所有特征。
2、正方形的四条边都相等,四个角都是直角。
3、正方形的对角线相等且互相垂直平分,并且每条对角线分别平分一组对角。
*
课堂作业:
P94 练习 2 . P98 习题 12. P104 8,9
如何设计花坛?
在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
请你来当设计师
*
正方形
19.3
*
一、教学目的
1.掌握正方形的概念、性质和判定,并会用它们进行有关的论证和计算.
2.理解正方形与平行四边形、矩形、菱形的联系和区别,提高学生的逻辑思维能力.
二、重点、难点
1.教学重点:正方形的定义及正方形与平行四边形、矩形、菱形的联系.
2.教学难点:正方形与矩形、菱形的关系及正方形性质与判定的灵活运用
*
正方形 自我介绍
在四边形的大家庭中,我有四个兄弟,
老大是平行四边形,它性格温和,
老二是菱形,它活泼可爱,
老三是矩形,他稳重大方,江湖上人称长方形,
我就是正方形老四,我集三位大哥的优点于一身,人见人爱。
*
平行四边形
正方形
一组邻边相等
一内角是直角
定义:有一个角是直角,且有一组邻边相等的平行四边形叫做正方形
*
对角线: 对角线相等且互相垂直平分,每条对角线平 分一组对角。
边: 对边平行,四边相等
角 :四个角都是直角
*
正方形的性质
=菱形的性质
+矩形的性质
老师:你觉得判断一个四边形是正方形有哪些方法?
*
平行四边形
正方形
一组邻边相等
一内角是直角
1、
正方形
菱形
2、
一内角是直角
矩形
3、
一组邻边相等
正方形
正方形的判定方法:
(可以平行四边形、矩形、菱形为基础)
定义法
菱形法
矩形法
*
√
√
√
×
(1)正方形的一条对角线把正方形分成两个全等的
等腰直角三角形( )
(2)对角线互相垂直且相等的四边形是正方形( )
(3)如果一个菱形的对角线相等,那么它一定
是正方形 ( )
(4)如果一个矩形的对角线互相垂直,那么它
一定是正方形 ( )
(5)四条边相等且有一个角是直角的四边形是正方形( )
√
仔细思考,判一判:
(6)四个角都相等的四边形是正方形 ( )
×
*
正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直平分.
C、对角互补.
D、对角线相等.
2.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等.
B
D
火眼金睛,选一选:
*
3.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正 方形的是:( ) A.AO=BO=CO=DO,AC⊥BD
B.AD∥BC ∠A=∠C
C.AO=CO BO=DO AB=BC
D.AC=BD
A
4 .四个内角都相等,四条边也都相等的四边形一定是:( )
A.正方形 B.菱形 C.矩形 D.平行四边形
A
*
1).已知:正方形ABCD对角线AC、BD相 交于点O,且AB=2cm,则AC= ,
正方形的面积S=______.
2
2
4
6
36
2).已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,
面积S=________.则边长AB=______,
例1:填空
*
1、如图,在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB (2) BH⊥AF
牛刀小试:
*
F
A
E
G
C
B
D
H
3
A
2
1
⌒
⌒
⌒
2、如图,△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。 求证:∠CEA=∠ABG
证明:∵四边形ABDE和四边形ACFG是正方形。 ∴AE=AB AG=AC ∠1=∠2=90° 又∵∠EAC=∠1+∠BAC=90°+∠BAC ∠BAG=∠2+∠BAC=90°+∠BAC ∴∠EAC=∠BAG ∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG
*
A
B
C
D
E
F
G
N
1
2
A
B
D
C
F
E
3、如图,在正方形ABCD中,E在BC的延长线上,且CE=AC,AE交CD于F,则求∠AFC的度数。
*
例2、 直角三角形ABC中,CD平分∠ACB交AB于D,DE⊥AC,DF⊥AB。求证:四边形CEDF是正方形。
A
B
C
D
E
F
∴四边形CEDF是正方形
( )
∴ DE=DF( )
DE⊥AC, DF⊥BC
∵ CD平分∠ACB
∴ 四边形ABCD为矩形
( )
而∠ACB=90°
∴ ∠DEC=90°, ∠DFC=90°
证明:∵ DE⊥AC,DF⊥AB
有三个角是直角的四边形是矩形
角平分线的定理
有一组邻边相等的矩形是正方形
*
*
如图,点A′B′C′D′分别是正方形ABCD四条边上的点,并且AA′=BB′=CC′=DD′.
求证:四边形A′B′C′D′是正方形。
D
C
A
B
D ′
A ′
C ′
B ′
3
2
1
证明:因为四边形ABCD是正方形,所以 AB=BC=CD=DA
∵ AA′=BB′=CC′=DD′.
∴ AD′=BA′=CB′=DC′.
∵ ∠A=∠B=∠C=∠D=90°
∴ △AA′D′≌△BB′A′≌△B′CC′≌△C′DD′.
∴B′A′=C′B′=D′C′=A′D′
∴ 四边形A′B′C′D′是菱形
又 ∵ ∠1= ∠3,
∠1+ ∠2=90°
∴ ∠3+ ∠2=90°
∴ 四边形A′B′C′D′是正方形
*
∴ ∠D′A′B′=90°
练一练:
课 堂 小 结
正方形的特征:
1、正方形是特殊的平行四边形,具备平行四边形的所有特征。
2、正方形的四条边都相等,四个角都是直角。
3、正方形的对角线相等且互相垂直平分,并且每条对角线分别平分一组对角。
*
课堂作业:
P94 练习 2 . P98 习题 12. P104 8,9
如何设计花坛?
在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
请你来当设计师
*
