沪科版数学八年级下册 20.2数据的集中趋势与离散程度-数据的离散程度-课件(共19张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 20.2数据的集中趋势与离散程度-数据的离散程度-课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 670.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-25 10:44:31 | ||
图片预览






文档简介
(共19张PPT)
数据的离散程度
数据的集中趋势与离散程度
问题6 两台机床都生产直径为(20+0.2)mm的零件,为了检验产品质量,从产品中各抽出10个进行测量,结果如下:
机床A 20.0 19.8 20.1 20.2 19.9 20.0 20.2 19.9 20.2 19.8
机床B 20.0 20.0 19.9 20.0 19.9 20.2 20.0 20.1 20.1 19.8
思考
根据以上结果评判哪台机床的零件的精度更稳定。
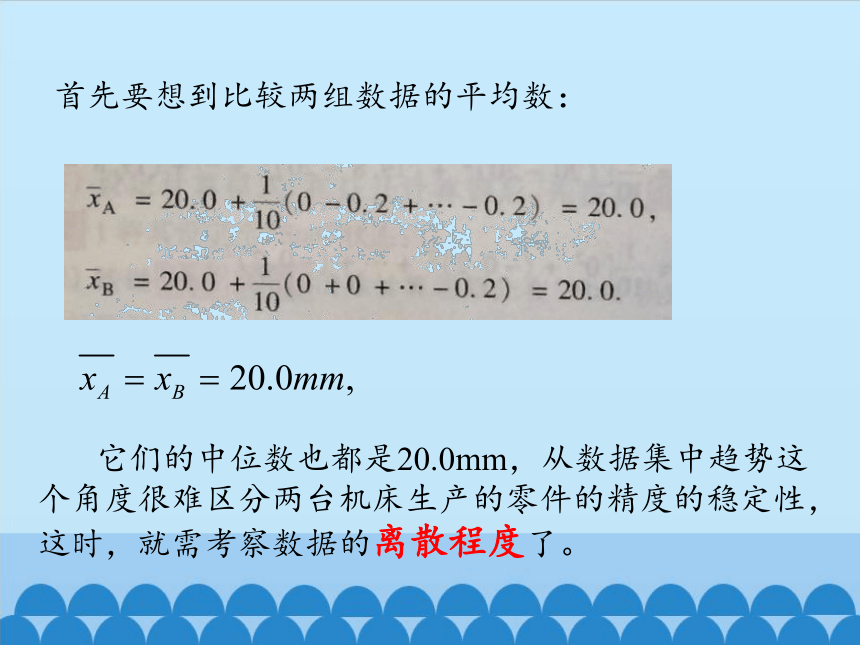
首先要想到比较两组数据的平均数:
它们的中位数也都是20.0mm,从数据集中趋势这个角度很难区分两台机床生产的零件的精度的稳定性,这时,就需考察数据的离散程度了。
把每组零件的直径分别用点来表示,如图:
容易看出机床B比机床A生产的零件的精度更稳定,如何用数量来刻画一组数据的离散程度呢?
机床A
机床B
在一组数据中,各数据与它们平均数的差的平方的平均数(即“先平均,再求差,然后平方,最后再平均”)得到的数叫方差。
1.方差是衡量数据稳定性的一个统计量;
2.方差的单位是所给数据单位的平方;
3.方差越大,波动越大,越不稳定;
方差越小,波动越小,越稳定。
S2= [ (x1-x)2+(x2-x)2+ +(xn-x)2 ]
方差
计算方差的一般步骤:
1.利用平均数公式计算这组数据的平均数X
2.利用方差公式计算这组数据的方差S2
S2= [ (x1-x)2+(x2-x)2+ +(xn-x)2 ]
下面通过计算方差,来判断问题中的机床B和机床A哪台生产的零件精度更稳定。
机床A 20.0 19.8 20.1 20.2 19.9 20.0 20.2 19.9 20.2 19.8
机床B 20.0 20.0 19.9 20.0 19.9 20.2 20.0 20.1 20.1 19.8
机床A 20.0 19.8 20.1 20.2 19.9 20.0 20.2 19.9 20.2 19.8
机床B 20.0 20.0 19.9 20.0 19.9 20.2 20.0 20.1 20.1 19.8
由于0.026>0.012,可知机床B比机床A生产的零件精度更稳定。
求一组数据的方差,用计算器更为方便。
例5 用计算器求下列数据的方差(结果保留2位小数):
138,156,131,141,128,139,135,130。
解 按键方法:
(1)设定计算模式,在打开计算机后,先按键
1将其设定至“Stat”状态;
(2)按键 清除计算器原先在“Stat”模式
下所储存的数据;
(3)输入数据,依次按以下各键:
138 156 131 141 128
139 135 130 ;
(4)求方差,在计算器的键盘上,用σX表示
一组数据的方差的算术平方根。
按键 显示方差的算术平方根:
按键 显示方差:
由上可得
数据的单位与方差的单位一致吗?
动动脑!
为了使单位一致,可用方差的算术平方根:
S = [ (x1-x)2+(x2-x)2+ +(xn-x)2 ]
来表示,并把它叫做标准差。
为了考察甲、乙两种小麦的长势,分别从中抽出10株苗,测得苗高如下(单位:cm):
甲:12 13 14 15 10 16 13 11 15 11
乙:11 16 17 14 13 19 6 8 10 16
哪种小麦长得比较整齐?
已知三组数据1、2、3、4、5;11、12、13、14、15和3、6、9、12、15。
1.求这三组数据的平均数、方差和标准差。
2.对照以上结果,你能从中发现哪些有趣的结论?
平均数 方差 标准差
1、2、3、4、5
11、12、13、14、15
3、6、9、12、15
3
2
13
2
9
18
探索发现
发现:有两组数据,设其平均数分别为 ,
,方差分别为 ,
(1)当第二组每个数据比第一组每个数据增加(或减少)m个单位时,
则有 = ±m,
=
(2)当第二组每个数据是第一组每个数据的n倍时,
则有 =n ,
=
已知数据x1、x2、x3、x4、x5的方差是 3,那么数据
x1-1,x2-1,x3-1,x4-1,x5-1的方差是( )
(A)1 (B)2
(C)3 (D)4
C
做一做:
1.方差:各数据与平均数的差的平方的平均数叫做这批数据的方差。
2.方差的意义:用来衡量一批数据的波动大小(即这批数据偏离平均数的大小)。即方差越大,说明数据的波动越大,越不稳定。
S2= [ (x1-x)2+(x2-x)2+ +(xn-x)2 ]
3.标准差:方差的算术平方根叫做标准差。
S = [ (x1-x)2+(x2-x)2+ +(xn-x)2 ]
计算一组数据的方差的一般步骤:
1.利用平均数公式计算这组数据的平均数X
2.利用方差公式计算这组数据的方差S2
作业:
1.课内练习
2.习题
谢 谢
数据的离散程度
数据的集中趋势与离散程度
问题6 两台机床都生产直径为(20+0.2)mm的零件,为了检验产品质量,从产品中各抽出10个进行测量,结果如下:
机床A 20.0 19.8 20.1 20.2 19.9 20.0 20.2 19.9 20.2 19.8
机床B 20.0 20.0 19.9 20.0 19.9 20.2 20.0 20.1 20.1 19.8
思考
根据以上结果评判哪台机床的零件的精度更稳定。
首先要想到比较两组数据的平均数:
它们的中位数也都是20.0mm,从数据集中趋势这个角度很难区分两台机床生产的零件的精度的稳定性,这时,就需考察数据的离散程度了。
把每组零件的直径分别用点来表示,如图:
容易看出机床B比机床A生产的零件的精度更稳定,如何用数量来刻画一组数据的离散程度呢?
机床A
机床B
在一组数据中,各数据与它们平均数的差的平方的平均数(即“先平均,再求差,然后平方,最后再平均”)得到的数叫方差。
1.方差是衡量数据稳定性的一个统计量;
2.方差的单位是所给数据单位的平方;
3.方差越大,波动越大,越不稳定;
方差越小,波动越小,越稳定。
S2= [ (x1-x)2+(x2-x)2+ +(xn-x)2 ]
方差
计算方差的一般步骤:
1.利用平均数公式计算这组数据的平均数X
2.利用方差公式计算这组数据的方差S2
S2= [ (x1-x)2+(x2-x)2+ +(xn-x)2 ]
下面通过计算方差,来判断问题中的机床B和机床A哪台生产的零件精度更稳定。
机床A 20.0 19.8 20.1 20.2 19.9 20.0 20.2 19.9 20.2 19.8
机床B 20.0 20.0 19.9 20.0 19.9 20.2 20.0 20.1 20.1 19.8
机床A 20.0 19.8 20.1 20.2 19.9 20.0 20.2 19.9 20.2 19.8
机床B 20.0 20.0 19.9 20.0 19.9 20.2 20.0 20.1 20.1 19.8
由于0.026>0.012,可知机床B比机床A生产的零件精度更稳定。
求一组数据的方差,用计算器更为方便。
例5 用计算器求下列数据的方差(结果保留2位小数):
138,156,131,141,128,139,135,130。
解 按键方法:
(1)设定计算模式,在打开计算机后,先按键
1将其设定至“Stat”状态;
(2)按键 清除计算器原先在“Stat”模式
下所储存的数据;
(3)输入数据,依次按以下各键:
138 156 131 141 128
139 135 130 ;
(4)求方差,在计算器的键盘上,用σX表示
一组数据的方差的算术平方根。
按键 显示方差的算术平方根:
按键 显示方差:
由上可得
数据的单位与方差的单位一致吗?
动动脑!
为了使单位一致,可用方差的算术平方根:
S = [ (x1-x)2+(x2-x)2+ +(xn-x)2 ]
来表示,并把它叫做标准差。
为了考察甲、乙两种小麦的长势,分别从中抽出10株苗,测得苗高如下(单位:cm):
甲:12 13 14 15 10 16 13 11 15 11
乙:11 16 17 14 13 19 6 8 10 16
哪种小麦长得比较整齐?
已知三组数据1、2、3、4、5;11、12、13、14、15和3、6、9、12、15。
1.求这三组数据的平均数、方差和标准差。
2.对照以上结果,你能从中发现哪些有趣的结论?
平均数 方差 标准差
1、2、3、4、5
11、12、13、14、15
3、6、9、12、15
3
2
13
2
9
18
探索发现
发现:有两组数据,设其平均数分别为 ,
,方差分别为 ,
(1)当第二组每个数据比第一组每个数据增加(或减少)m个单位时,
则有 = ±m,
=
(2)当第二组每个数据是第一组每个数据的n倍时,
则有 =n ,
=
已知数据x1、x2、x3、x4、x5的方差是 3,那么数据
x1-1,x2-1,x3-1,x4-1,x5-1的方差是( )
(A)1 (B)2
(C)3 (D)4
C
做一做:
1.方差:各数据与平均数的差的平方的平均数叫做这批数据的方差。
2.方差的意义:用来衡量一批数据的波动大小(即这批数据偏离平均数的大小)。即方差越大,说明数据的波动越大,越不稳定。
S2= [ (x1-x)2+(x2-x)2+ +(xn-x)2 ]
3.标准差:方差的算术平方根叫做标准差。
S = [ (x1-x)2+(x2-x)2+ +(xn-x)2 ]
计算一组数据的方差的一般步骤:
1.利用平均数公式计算这组数据的平均数X
2.利用方差公式计算这组数据的方差S2
作业:
1.课内练习
2.习题
谢 谢
