沪科版数学八年级下册 19.3 矩形及矩形的性质 课件(共18张)
文档属性
| 名称 | 沪科版数学八年级下册 19.3 矩形及矩形的性质 课件(共18张) |
|
|
| 格式 | pptx | ||
| 文件大小 | 392.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-25 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
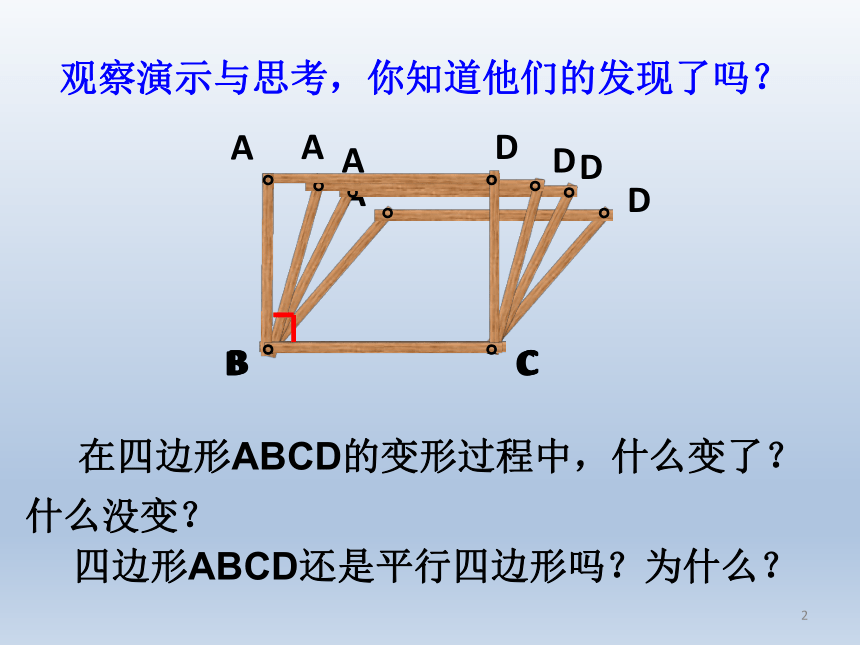
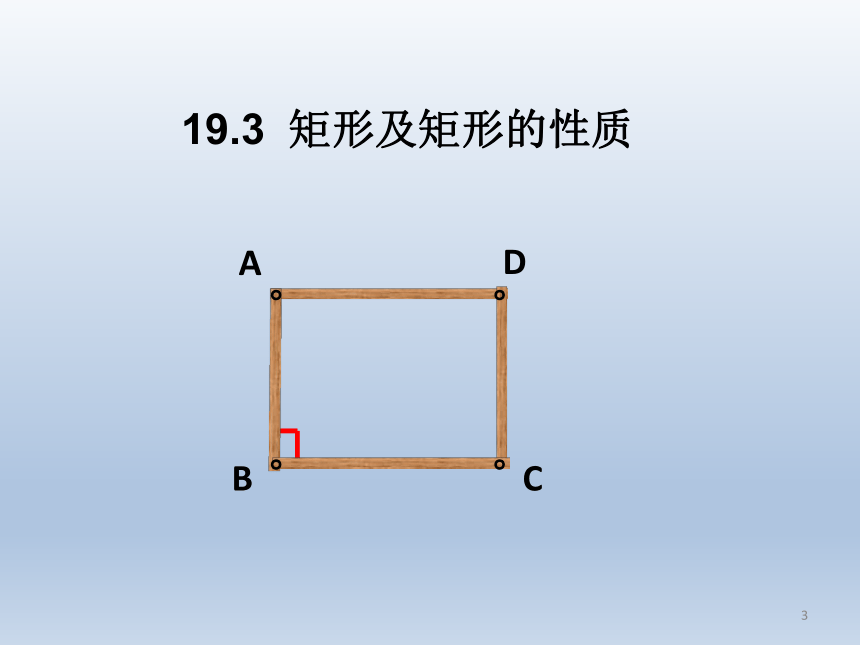
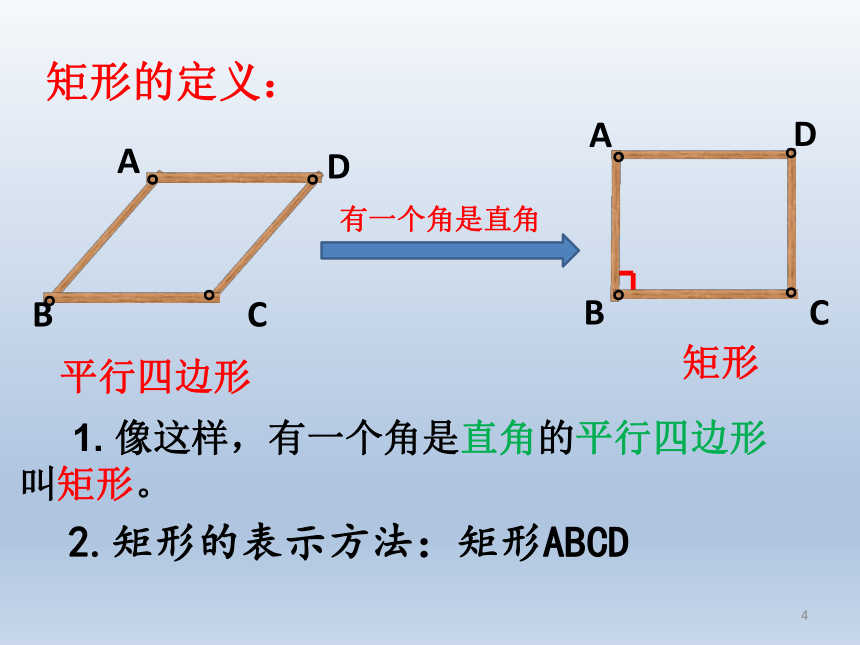
一天,爱动脑筋的小丽拿着小明做的平行四边模型进行研究时,惊奇的发现一种比较熟悉的四边形,她急忙喊来小辉、小明等几位数学爱好者进行研究。竟然惊喜的研究出它的好多性质,真是意想不到的收获。他们究竟发现了什么呢?。。。。ADCB。。。。ADCB观察演示与思考,你知道他们的发现了吗?。。。。ADCB。。。。ADCB。。。。ADCB在四边形ABCD的变形过程中,什么变了?什么没变?四边形ABCD还是平行四边形吗?为什么?19.3矩形及矩形的性质。。。。ADCB。。。。ADCB。。。。ADCB平行四边形有一个角是直角矩形矩形的定义:1.像这样,有一个角是直角的平行四边形叫矩形。2.矩形的表示方法:矩形ABCD想一想:
你能举出在学习和日常生活和生产实践中,有哪些东西是矩形的?
木门
纸张
电脑显示器
小丽:我发现,矩形就是特殊的平行四边形。因为矩形具有平行四边形的判定条件。小明:那么矩形必定具有平行四边形的所有的性质。1、矩形的两组对边分别平行且相等2、矩形的两组对角相等、邻角互补3、矩形两条对角线互相平分小方:既然矩形是特殊的平行四边形,那么矩形还有什么特殊的性质呢?小辉:我发现矩形的四个角都是直角。因为……BADC矩形的性质1:研究角的性质矩形的四个角都是直角.几何语言:∵四边形ABCD为矩形∴∠A=∠B=∠C=∠D=90°小宁看大家讨论的兴致很高,也加入了讨论,竟发现了新情况。小宁:我发现矩形的两条对角线是相等的。因为……已知:四边形ABCD是矩形求证:AC = BDABCD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC,BC = CB∴△ABC≌△DCB∴AC = BDO矩形的性质2:矩形的对角线相等符号语言:ABCD∵四边形ABCD是矩形∴AC = BDO正当大家沉浸在得出矩形的性质兴奋之中时,忽然小阳说:“我又发现一个结论:直角三角形斜边上的中线等于斜边的一半。 ”“因为根据平行四边形和矩形对角线的性质… … ”已知:在Rt△ABC中,∠ABC=900,BO是AC上的中线.求证: BO = AC.CBA证明:延长BO至D,使OD=BO,连结AD、DC.∵AO=OC, BO=OD∴四边形ABCD是平行四边形.∵∠ABC=900∴ ABCD是矩形∴AC=BD1212∴BO= BD= AC证明如下:DO直角三角形又一个性质:直角三角形斜边上的中线等于斜边的一半.符号语言:∵在Rt△ABC中,BO是斜边AC上的中线∴BO= ACCBAO例1:已知:矩形ABCD的两条对角线相交于O,∠AOD=120°,AB = 4cm.求矩形对角线的长.ABCDODCBA┓例2:已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线.(1)若BD=3㎝,则AC=______ ㎝;(2)若∠C=30°,AB=5㎝,则AC=_____㎝,BD=_____㎝.6510 1.矩形具有而一般平行四边形不具有的性质是()A.对角相等B.对边相等C.对角线相等D.对角线互相平分C牛刀小试:E.四个角的和是360°2.四边形ABCD是矩形1).若已知AB=8㎝,AD=6㎝,则AC=_______ ㎝ OB=_______ ㎝2).若已知AC=10㎝,BC=6㎝,则矩形的周长=____ cm,矩形的面积=_______㎝23).若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm,AB=_____cmODCBA510448284).直角三角形两直角边为5和12,则斜边上的中线长为.6.5牛刀小试:1.矩形的定义2.矩形的性质3.推论:直角三角形斜边上的中线等于斜边的一半课堂小结一个角是直角矩形两组对边分别平行平行四边形四边形(1)对边平行且相等;(2)四个角都是直角;(3)对角线互相平分且相等;作业:教材P88练习1,2两题教材P97习题19.3 1,2两题1. 如图,在四边形ABCD中∠ABC=∠ADC=900,M、N分别是AC、BD的中点。求证: MB=MD;MN⊥BD.●●拓展提高拓展提高2.如下图,BD,CE是△ABC的高,G,F分别是BC,DE的中点,求证:FG⊥DE..
一天,爱动脑筋的小丽拿着小明做的平行四边模型进行研究时,惊奇的发现一种比较熟悉的四边形,她急忙喊来小辉、小明等几位数学爱好者进行研究。竟然惊喜的研究出它的好多性质,真是意想不到的收获。他们究竟发现了什么呢?。。。。ADCB。。。。ADCB观察演示与思考,你知道他们的发现了吗?。。。。ADCB。。。。ADCB。。。。ADCB在四边形ABCD的变形过程中,什么变了?什么没变?四边形ABCD还是平行四边形吗?为什么?19.3矩形及矩形的性质。。。。ADCB。。。。ADCB。。。。ADCB平行四边形有一个角是直角矩形矩形的定义:1.像这样,有一个角是直角的平行四边形叫矩形。2.矩形的表示方法:矩形ABCD想一想:
你能举出在学习和日常生活和生产实践中,有哪些东西是矩形的?
木门
纸张
电脑显示器
小丽:我发现,矩形就是特殊的平行四边形。因为矩形具有平行四边形的判定条件。小明:那么矩形必定具有平行四边形的所有的性质。1、矩形的两组对边分别平行且相等2、矩形的两组对角相等、邻角互补3、矩形两条对角线互相平分小方:既然矩形是特殊的平行四边形,那么矩形还有什么特殊的性质呢?小辉:我发现矩形的四个角都是直角。因为……BADC矩形的性质1:研究角的性质矩形的四个角都是直角.几何语言:∵四边形ABCD为矩形∴∠A=∠B=∠C=∠D=90°小宁看大家讨论的兴致很高,也加入了讨论,竟发现了新情况。小宁:我发现矩形的两条对角线是相等的。因为……已知:四边形ABCD是矩形求证:AC = BDABCD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC,BC = CB∴△ABC≌△DCB∴AC = BDO矩形的性质2:矩形的对角线相等符号语言:ABCD∵四边形ABCD是矩形∴AC = BDO正当大家沉浸在得出矩形的性质兴奋之中时,忽然小阳说:“我又发现一个结论:直角三角形斜边上的中线等于斜边的一半。 ”“因为根据平行四边形和矩形对角线的性质… … ”已知:在Rt△ABC中,∠ABC=900,BO是AC上的中线.求证: BO = AC.CBA证明:延长BO至D,使OD=BO,连结AD、DC.∵AO=OC, BO=OD∴四边形ABCD是平行四边形.∵∠ABC=900∴ ABCD是矩形∴AC=BD1212∴BO= BD= AC证明如下:DO直角三角形又一个性质:直角三角形斜边上的中线等于斜边的一半.符号语言:∵在Rt△ABC中,BO是斜边AC上的中线∴BO= ACCBAO例1:已知:矩形ABCD的两条对角线相交于O,∠AOD=120°,AB = 4cm.求矩形对角线的长.ABCDODCBA┓例2:已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线.(1)若BD=3㎝,则AC=______ ㎝;(2)若∠C=30°,AB=5㎝,则AC=_____㎝,BD=_____㎝.6510 1.矩形具有而一般平行四边形不具有的性质是()A.对角相等B.对边相等C.对角线相等D.对角线互相平分C牛刀小试:E.四个角的和是360°2.四边形ABCD是矩形1).若已知AB=8㎝,AD=6㎝,则AC=_______ ㎝ OB=_______ ㎝2).若已知AC=10㎝,BC=6㎝,则矩形的周长=____ cm,矩形的面积=_______㎝23).若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm,AB=_____cmODCBA510448284).直角三角形两直角边为5和12,则斜边上的中线长为.6.5牛刀小试:1.矩形的定义2.矩形的性质3.推论:直角三角形斜边上的中线等于斜边的一半课堂小结一个角是直角矩形两组对边分别平行平行四边形四边形(1)对边平行且相等;(2)四个角都是直角;(3)对角线互相平分且相等;作业:教材P88练习1,2两题教材P97习题19.3 1,2两题1. 如图,在四边形ABCD中∠ABC=∠ADC=900,M、N分别是AC、BD的中点。求证: MB=MD;MN⊥BD.●●拓展提高拓展提高2.如下图,BD,CE是△ABC的高,G,F分别是BC,DE的中点,求证:FG⊥DE..
