沪科版数学八年级下册 17.1 一元二次方程 教案(表格式)
文档属性
| 名称 | 沪科版数学八年级下册 17.1 一元二次方程 教案(表格式) | 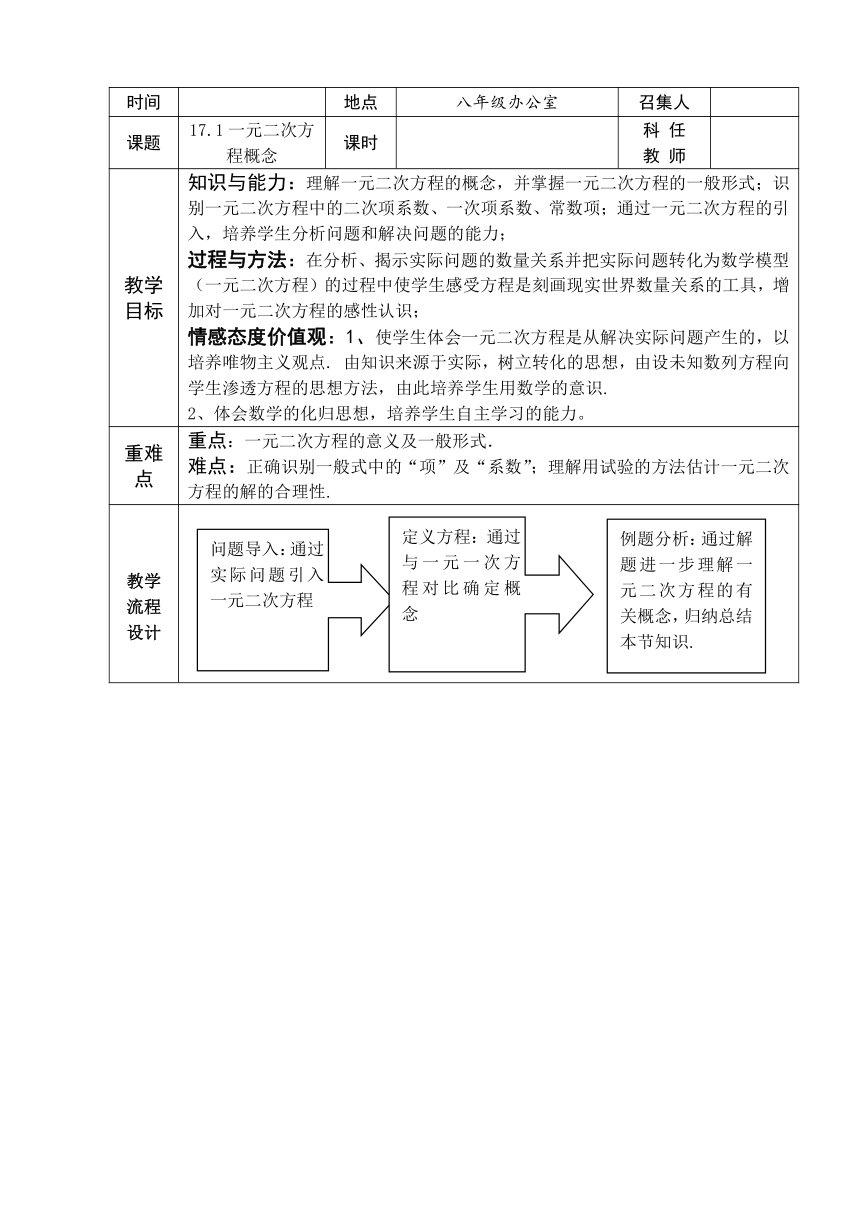 | |
| 格式 | docx | ||
| 文件大小 | 63.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-25 14:33:53 | ||
图片预览


文档简介
时间 地点 八年级办公室 召集人
课题 17.1一元二次方程概念 课时 科 任 教 师
教学 目标 知识与能力:理解一元二次方程的概念,并掌握一元二次方程的一般形式;识别一元二次方程中的二次项系数、一次项系数、常数项;通过一元二次方程的引入,培养学生分析问题和解决问题的能力; 过程与方法:在分析、揭示实际问题的数量关系并把实际问题转化为数学模型(一元二次方程)的过程中使学生感受方程是刻画现实世界数量关系的工具,增加对一元二次方程的感性认识; 情感态度价值观:1、使学生体会一元二次方程是从解决实际问题产生的,以培养唯物主义观点. 由知识来源于实际,树立转化的思想,由设未知数列方程向学生渗透方程的思想方法,由此培养学生用数学的意识. 2、体会数学的化归思想,培养学生自主学习的能力。
重难点 重点:一元二次方程的意义及一般形式. 难点:正确识别一般式中的“项”及“系数”;理解用试验的方法估计一元二次方程的解的合理性.
教学流程设计 (
问题导入:通过实际问题引入一元二次方程
定义方程:通过与一元一次方程对比确定概念
例题分析:通过解题进一步理解一元二次方程的有关概念,归纳总结本节知识.
)
教 学 过 程 教 学 过 程 一、知识回顾: 1.你还记得什么叫方程?什么叫方程的解吗? 2.什么是一元一次方程?它的 一般形式是什么? 3.下面的方程(组),你还认识吗? 二、创设问题情景 问题1 今天是个特别的日子,听班主任说我们班有好多人的生日都在今天.我特别的高兴,恰好老师的生日也在今天。为庆祝生日,我们凡是生日在今天的相互都送礼物,我们都不能吝啬啊,结果我们一共送了56件礼物,那知道今天我们班一共有多少人今天过生日? 分析:设一共有x人过生日,由已知知道,每个过生日的人要买(x-1)件礼物,即共买x(x-1)件. 不难列出方程 由题意得 x(x-1)=56 整理可得, x2-x-56=0.………(1) 问题2 为美化、绿化校园,增强学校的办学品位。我们移村中学准备在大操场南头,开辟面积为900㎡的一块长方形绿地,并且长比宽多10m,则绿地的长和宽各为多少 分析: 设长方形绿地的宽为xm,则长方形绿地的长为(x+10)m.根据题意,可列得方程 x(x+10)=900, 整理可得, x2+10x-900=0. ………(2) 三、探索新知 通过以上的分析和思考,问题1和问题2分别归纳为解方程(1)和(2),并结合2x2-33x+58=0,x2+2x-1=0.显然,这几个方程都不是一元一次方程,我们先来研究这两个方程与一元一次方程有什么异同点,以后再研究如何解决这类方程. 问题1:以上两个方程与一元一次方程的区别在哪里? 问题2:他们有什么共同点呢?(引导学生观察、思考、讨论后回答) 问题3:你能类比一元一次方程给上面两个方程起个名称吗? (一元二次方程,教师板书) 问题4:根据以上讨论的结果,能不能给一元二次方程下个定义吗? 归纳为:只含有一个未知数,并且未知数的最高次数是2的整式方程,叫做一元二次方程. 【说明】一元二次方程通常写成如下一般形式: ax2+bx+c=0(a、b、c是已知数,a≠0),其中ax2叫做二次项, a是二次项系数;bx叫做一次项,b是一次项系数; c叫做常数项. 提问:分别说出方程(1)(2)的二次项系数、一次项系数和常数项. 四、例题讲解巩固 例1 判断下列方程是否为一元二次方程? (1)3x+2=5y; (2) x=4 (3) . (4) x-4=(x+2) 下列方程中哪些是一元二次方程? 例2 将方程3x (x-1) = 2(x-2)-4 化为一元二次方程的一般形式,并写出二次项系数、一次项系数及常数项。 解 :去括号得:3 x-3x=2x-4-4 移项,合并同类项,整理得,3x-5x+8=0. 二次项是3x,二次项系数是3;一次项是-5x,一次项系数是-5;常数项是8. 五、课堂练习 1、填写下列表格 方程一般形式二次项系数一交次项系数常数项4x=3x(x-1)2-9=0x (x+2)=3(x+2)
2、方程(2a- 4)x2 —2bx+a=0, 在什么条件下此方程为一元二次方程?在什么条件下此方程为一元一次方程? 解:当(2a- 4)≠0,即a≠2时是一元二次方程; 当(2a- 4)=0,—2b≠0,即a=2,b≠0时是一元一次方程; 六、议一议 通过以上习题的练习的情况,你认为在确定一元二次方程的各项系数及常数项的时候,需要注意哪些? 在确定一元二次方程的二次项系数、一次项系数和常数项时,必须把方程化为一般形式才能进行。 二次项系数、一次项系数以及常数项都要连同它前面的符号. 二次项系数a≠0. 七、课堂小结 1、什么样的方程叫做一元二次方程. 2、一元二次方程的一般形式怎么表示? 3、一元二次方程二次项系数可以是任意实数吗? 4、如何确定一元二次方程一次项系数和常数项? 5、本节课你有哪些收获?困惑?与大家交流、分享. 八、作业布置 课本习题:2、3 讨论补充记录 讨论补充记录
板书 设计 17.1一元二次方程(1) 一、知识回顾: 五、课堂练习 二、创设问题情景 六、议一议 三、探索新知 七、课堂小结 四、例题讲解巩固 八、作业布置
课题 17.1一元二次方程概念 课时 科 任 教 师
教学 目标 知识与能力:理解一元二次方程的概念,并掌握一元二次方程的一般形式;识别一元二次方程中的二次项系数、一次项系数、常数项;通过一元二次方程的引入,培养学生分析问题和解决问题的能力; 过程与方法:在分析、揭示实际问题的数量关系并把实际问题转化为数学模型(一元二次方程)的过程中使学生感受方程是刻画现实世界数量关系的工具,增加对一元二次方程的感性认识; 情感态度价值观:1、使学生体会一元二次方程是从解决实际问题产生的,以培养唯物主义观点. 由知识来源于实际,树立转化的思想,由设未知数列方程向学生渗透方程的思想方法,由此培养学生用数学的意识. 2、体会数学的化归思想,培养学生自主学习的能力。
重难点 重点:一元二次方程的意义及一般形式. 难点:正确识别一般式中的“项”及“系数”;理解用试验的方法估计一元二次方程的解的合理性.
教学流程设计 (
问题导入:通过实际问题引入一元二次方程
定义方程:通过与一元一次方程对比确定概念
例题分析:通过解题进一步理解一元二次方程的有关概念,归纳总结本节知识.
)
教 学 过 程 教 学 过 程 一、知识回顾: 1.你还记得什么叫方程?什么叫方程的解吗? 2.什么是一元一次方程?它的 一般形式是什么? 3.下面的方程(组),你还认识吗? 二、创设问题情景 问题1 今天是个特别的日子,听班主任说我们班有好多人的生日都在今天.我特别的高兴,恰好老师的生日也在今天。为庆祝生日,我们凡是生日在今天的相互都送礼物,我们都不能吝啬啊,结果我们一共送了56件礼物,那知道今天我们班一共有多少人今天过生日? 分析:设一共有x人过生日,由已知知道,每个过生日的人要买(x-1)件礼物,即共买x(x-1)件. 不难列出方程 由题意得 x(x-1)=56 整理可得, x2-x-56=0.………(1) 问题2 为美化、绿化校园,增强学校的办学品位。我们移村中学准备在大操场南头,开辟面积为900㎡的一块长方形绿地,并且长比宽多10m,则绿地的长和宽各为多少 分析: 设长方形绿地的宽为xm,则长方形绿地的长为(x+10)m.根据题意,可列得方程 x(x+10)=900, 整理可得, x2+10x-900=0. ………(2) 三、探索新知 通过以上的分析和思考,问题1和问题2分别归纳为解方程(1)和(2),并结合2x2-33x+58=0,x2+2x-1=0.显然,这几个方程都不是一元一次方程,我们先来研究这两个方程与一元一次方程有什么异同点,以后再研究如何解决这类方程. 问题1:以上两个方程与一元一次方程的区别在哪里? 问题2:他们有什么共同点呢?(引导学生观察、思考、讨论后回答) 问题3:你能类比一元一次方程给上面两个方程起个名称吗? (一元二次方程,教师板书) 问题4:根据以上讨论的结果,能不能给一元二次方程下个定义吗? 归纳为:只含有一个未知数,并且未知数的最高次数是2的整式方程,叫做一元二次方程. 【说明】一元二次方程通常写成如下一般形式: ax2+bx+c=0(a、b、c是已知数,a≠0),其中ax2叫做二次项, a是二次项系数;bx叫做一次项,b是一次项系数; c叫做常数项. 提问:分别说出方程(1)(2)的二次项系数、一次项系数和常数项. 四、例题讲解巩固 例1 判断下列方程是否为一元二次方程? (1)3x+2=5y; (2) x=4 (3) . (4) x-4=(x+2) 下列方程中哪些是一元二次方程? 例2 将方程3x (x-1) = 2(x-2)-4 化为一元二次方程的一般形式,并写出二次项系数、一次项系数及常数项。 解 :去括号得:3 x-3x=2x-4-4 移项,合并同类项,整理得,3x-5x+8=0. 二次项是3x,二次项系数是3;一次项是-5x,一次项系数是-5;常数项是8. 五、课堂练习 1、填写下列表格 方程一般形式二次项系数一交次项系数常数项4x=3x(x-1)2-9=0x (x+2)=3(x+2)
2、方程(2a- 4)x2 —2bx+a=0, 在什么条件下此方程为一元二次方程?在什么条件下此方程为一元一次方程? 解:当(2a- 4)≠0,即a≠2时是一元二次方程; 当(2a- 4)=0,—2b≠0,即a=2,b≠0时是一元一次方程; 六、议一议 通过以上习题的练习的情况,你认为在确定一元二次方程的各项系数及常数项的时候,需要注意哪些? 在确定一元二次方程的二次项系数、一次项系数和常数项时,必须把方程化为一般形式才能进行。 二次项系数、一次项系数以及常数项都要连同它前面的符号. 二次项系数a≠0. 七、课堂小结 1、什么样的方程叫做一元二次方程. 2、一元二次方程的一般形式怎么表示? 3、一元二次方程二次项系数可以是任意实数吗? 4、如何确定一元二次方程一次项系数和常数项? 5、本节课你有哪些收获?困惑?与大家交流、分享. 八、作业布置 课本习题:2、3 讨论补充记录 讨论补充记录
板书 设计 17.1一元二次方程(1) 一、知识回顾: 五、课堂练习 二、创设问题情景 六、议一议 三、探索新知 七、课堂小结 四、例题讲解巩固 八、作业布置
