江西省南昌市八一中学、洪都中学、麻丘中学2012-2013学年高二下学期期中联考数学(文)试题
文档属性
| 名称 | 江西省南昌市八一中学、洪都中学、麻丘中学2012-2013学年高二下学期期中联考数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 192.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-20 11:25:40 | ||
图片预览



文档简介
南昌市八一中学、洪都中学、麻丘中学2012-2013学年高二下学期期中联考
数学文试题
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、在正方体中,下列几种说法正确的是 ( )
A、 B、 C、与成角 D、与成角
2. a,b,c表示直线,M表示平面,给出下列四个命题:①若a∥M,b∥M,则a∥b;
②若bM,a∥b,则a∥M;③若a⊥c,b⊥c,则a∥b;④若a⊥M,b⊥M,则a∥b.其中正确命题的个数有 ( )
A、0个 B、1个 C、2个 D、3个
3. 如图:直三棱柱ABC—A1B1C1的体积为V,点P、Q分别在侧棱AA1和
CC1上,AP=C1Q,则四棱锥B—APQC的体积为 ( )
A、 B、 C、 D、
4. 下列命题是真命题的为 ( )
A.若,则 B.若,则
C.若,则 D.若,则
5. 设的( )
A 充分不必要条件 B 必要不充分条件 C充要条件 D既不充分也不必要条件
6. 命题“存在R,0”的否定是( )
A. 不存在R, >0 B. 存在R, 0
C. 对任意的R, 0 D. 对任意的R, >0
7.一正四棱锥的高为2,侧棱与底面所成的角为45°,则这一正四棱锥的斜高等于( )
A.2 B. C.4 D.2
8 . P为矩形ABCD所在平面外一点,且PA⊥平面ABCD,P到B,C,D三点的距离分别是,,,则P到A点的距离是 ( )
(A)1 (B)2 (C) (D)4
9. 已知命题,命题恒成立。若为假命题,则实数的取值范围为( )
A、 B、或> -1 C、 D、
10. 曲线在处的切线平行于直线,则点的坐标为( )
A B
C 和 D 和
二、填空题(共5小题,每小题5分)
曲线在点 处的切线倾斜角为__________
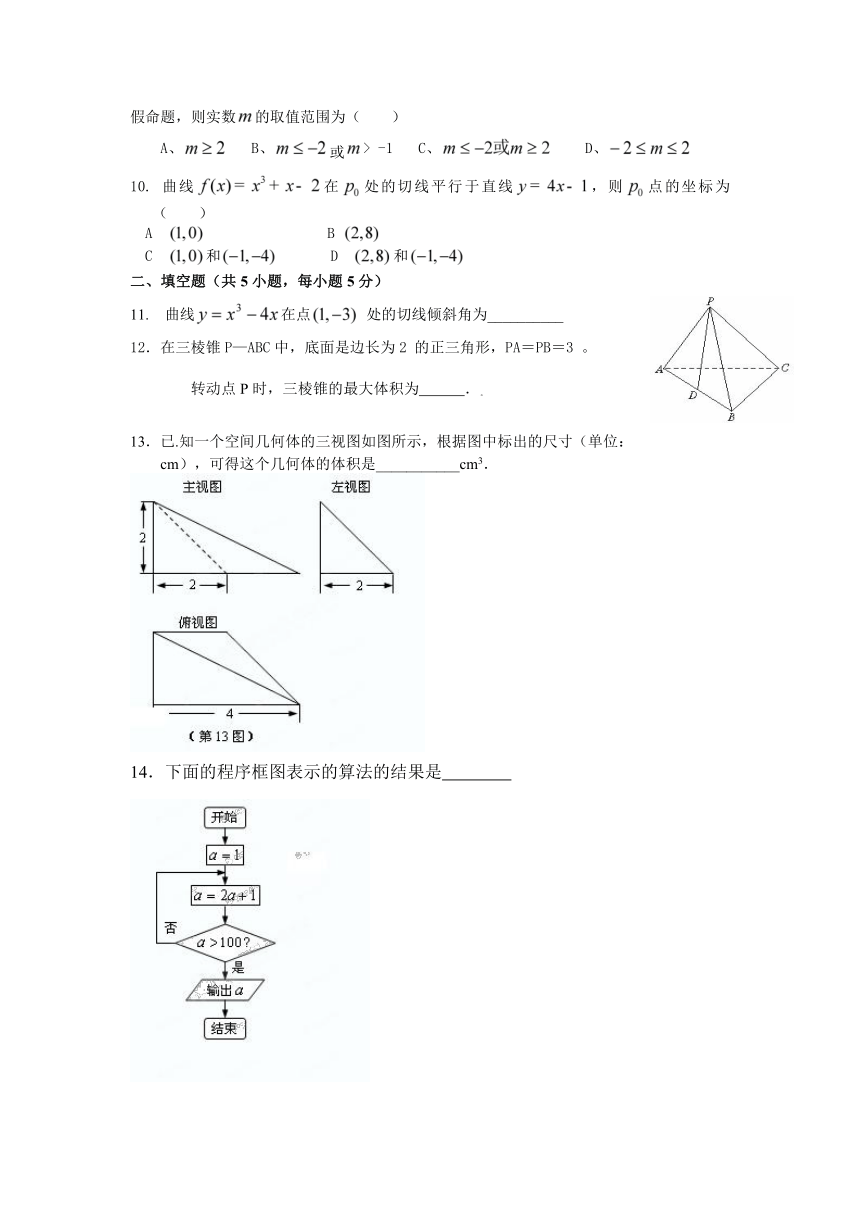
12.在三棱锥P—ABC中,底面是边长为2 的正三角形,PA=PB=3 。
转动点P时,三棱锥的最大体积为 .。
13.已.知一个空间几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是___________cm3.
14.下面的程序框图表示的算法的结果是
15.若命题“”是假命题,则实数的取值范围为_______,
三、解答题:(12分+12分+12分+12分+13分+14分)
16. 已知命题P:函数在定义域上单调递增;
命题Q:不等式对任意实数恒成立。
若是真命题,求实数的取值范围
17.ABCD为直角梯形,∠DAB=∠ABC=90°,AB=BC=a,AD=2a,PA⊥平面ABCD,PA=a,
(1)求证:PC⊥CD;(2)求点B到直线PC的距离。
18. 已知正三棱柱ABC-A1B1C1的底面边长为8,侧棱长为6,D为AC中点。
(1)求证:直线AB1∥平面C1DB;
(2)求异面直线AB1与BC1所成角的余弦值。
19. 如图,四边形ABCD是正方形,PB⊥平面ABCD,MA//PB,PB=AB=2MA,
(Ⅰ)证明:AC//平面PMD;
(Ⅱ)求直线BD与平面PCD所成的角的大小;
20.已知函数在与时都取得极值
(1)求的值与函数的单调区间
(2)若对,不等式恒成立,求的取值范围
21. 已知斜三棱柱,,,在底面上的射影恰为的中点,又知。
(I)求证:平面;
(II)求到平面的距离;
高二文科数学参考答案
17. 17.
18证明:(1)连BC交于E,连DE, 则DE∥,
而DE面CDB,面CDB, ∴
(2)由(1)知∠DEB为异面直线所成的角,在
。
19.(Ⅰ)证明:如图1,取PD的中点E,连EO,EM。
∵EO//PB,EO=PB,MA//PB,MA=PB,
∴EO//MA,且EO=MA
∴四边形MAOE是平行四边形,
∴ME//AC 。
又∵AC平面PMD,ME平面PMD,
∴AC//平面PMD 。
(Ⅱ)如图1,PB⊥平面ABCD,
CD平面ABCD, ∴CD⊥PB。
又∵CD⊥BC, ∴CD⊥平面PBC。
∵CD平面PCD, ∴平面PBC⊥平面PCD。
过B作BF⊥PC于F,则BF⊥平面PDC,连DF,
则DF为BD在平面PCD上的射影。
∴∠BDF是直线BD与平面PDC所成的角。
不妨设AB=2,则在Rt△BFD中,, ∴∠BDF=
∴直线BD与平面PCD所成的角是
20.解:(1)
由,得
,函数的单调区间如下表:
(
极大值
(
极小值
(
所以函数的递增区间是与,递减区间是;
(2),当时,
为极大值,而,则为最大值,要使
恒成立,则只需要,得
21.解:(I)因为平面,
所以平面平面,
又,所以平面,
得,又
所以平面;
(II)因为,所以四边形为
菱形,
数学文试题
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、在正方体中,下列几种说法正确的是 ( )
A、 B、 C、与成角 D、与成角
2. a,b,c表示直线,M表示平面,给出下列四个命题:①若a∥M,b∥M,则a∥b;
②若bM,a∥b,则a∥M;③若a⊥c,b⊥c,则a∥b;④若a⊥M,b⊥M,则a∥b.其中正确命题的个数有 ( )
A、0个 B、1个 C、2个 D、3个
3. 如图:直三棱柱ABC—A1B1C1的体积为V,点P、Q分别在侧棱AA1和
CC1上,AP=C1Q,则四棱锥B—APQC的体积为 ( )
A、 B、 C、 D、
4. 下列命题是真命题的为 ( )
A.若,则 B.若,则
C.若,则 D.若,则
5. 设的( )
A 充分不必要条件 B 必要不充分条件 C充要条件 D既不充分也不必要条件
6. 命题“存在R,0”的否定是( )
A. 不存在R, >0 B. 存在R, 0
C. 对任意的R, 0 D. 对任意的R, >0
7.一正四棱锥的高为2,侧棱与底面所成的角为45°,则这一正四棱锥的斜高等于( )
A.2 B. C.4 D.2
8 . P为矩形ABCD所在平面外一点,且PA⊥平面ABCD,P到B,C,D三点的距离分别是,,,则P到A点的距离是 ( )
(A)1 (B)2 (C) (D)4
9. 已知命题,命题恒成立。若为假命题,则实数的取值范围为( )
A、 B、或> -1 C、 D、
10. 曲线在处的切线平行于直线,则点的坐标为( )
A B
C 和 D 和
二、填空题(共5小题,每小题5分)
曲线在点 处的切线倾斜角为__________
12.在三棱锥P—ABC中,底面是边长为2 的正三角形,PA=PB=3 。
转动点P时,三棱锥的最大体积为 .。
13.已.知一个空间几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是___________cm3.
14.下面的程序框图表示的算法的结果是
15.若命题“”是假命题,则实数的取值范围为_______,
三、解答题:(12分+12分+12分+12分+13分+14分)
16. 已知命题P:函数在定义域上单调递增;
命题Q:不等式对任意实数恒成立。
若是真命题,求实数的取值范围
17.ABCD为直角梯形,∠DAB=∠ABC=90°,AB=BC=a,AD=2a,PA⊥平面ABCD,PA=a,
(1)求证:PC⊥CD;(2)求点B到直线PC的距离。
18. 已知正三棱柱ABC-A1B1C1的底面边长为8,侧棱长为6,D为AC中点。
(1)求证:直线AB1∥平面C1DB;
(2)求异面直线AB1与BC1所成角的余弦值。
19. 如图,四边形ABCD是正方形,PB⊥平面ABCD,MA//PB,PB=AB=2MA,
(Ⅰ)证明:AC//平面PMD;
(Ⅱ)求直线BD与平面PCD所成的角的大小;
20.已知函数在与时都取得极值
(1)求的值与函数的单调区间
(2)若对,不等式恒成立,求的取值范围
21. 已知斜三棱柱,,,在底面上的射影恰为的中点,又知。
(I)求证:平面;
(II)求到平面的距离;
高二文科数学参考答案
17. 17.
18证明:(1)连BC交于E,连DE, 则DE∥,
而DE面CDB,面CDB, ∴
(2)由(1)知∠DEB为异面直线所成的角,在
。
19.(Ⅰ)证明:如图1,取PD的中点E,连EO,EM。
∵EO//PB,EO=PB,MA//PB,MA=PB,
∴EO//MA,且EO=MA
∴四边形MAOE是平行四边形,
∴ME//AC 。
又∵AC平面PMD,ME平面PMD,
∴AC//平面PMD 。
(Ⅱ)如图1,PB⊥平面ABCD,
CD平面ABCD, ∴CD⊥PB。
又∵CD⊥BC, ∴CD⊥平面PBC。
∵CD平面PCD, ∴平面PBC⊥平面PCD。
过B作BF⊥PC于F,则BF⊥平面PDC,连DF,
则DF为BD在平面PCD上的射影。
∴∠BDF是直线BD与平面PDC所成的角。
不妨设AB=2,则在Rt△BFD中,, ∴∠BDF=
∴直线BD与平面PCD所成的角是
20.解:(1)
由,得
,函数的单调区间如下表:
(
极大值
(
极小值
(
所以函数的递增区间是与,递减区间是;
(2),当时,
为极大值,而,则为最大值,要使
恒成立,则只需要,得
21.解:(I)因为平面,
所以平面平面,
又,所以平面,
得,又
所以平面;
(II)因为,所以四边形为
菱形,
同课章节目录
