2021-2022学年高一下学期物理人教版(2019)必修第二册第六章圆周运动基础知识点小结(word版教案)
文档属性
| 名称 | 2021-2022学年高一下学期物理人教版(2019)必修第二册第六章圆周运动基础知识点小结(word版教案) |  | |
| 格式 | zip | ||
| 文件大小 | 215.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-25 08:58:34 | ||
图片预览



文档简介
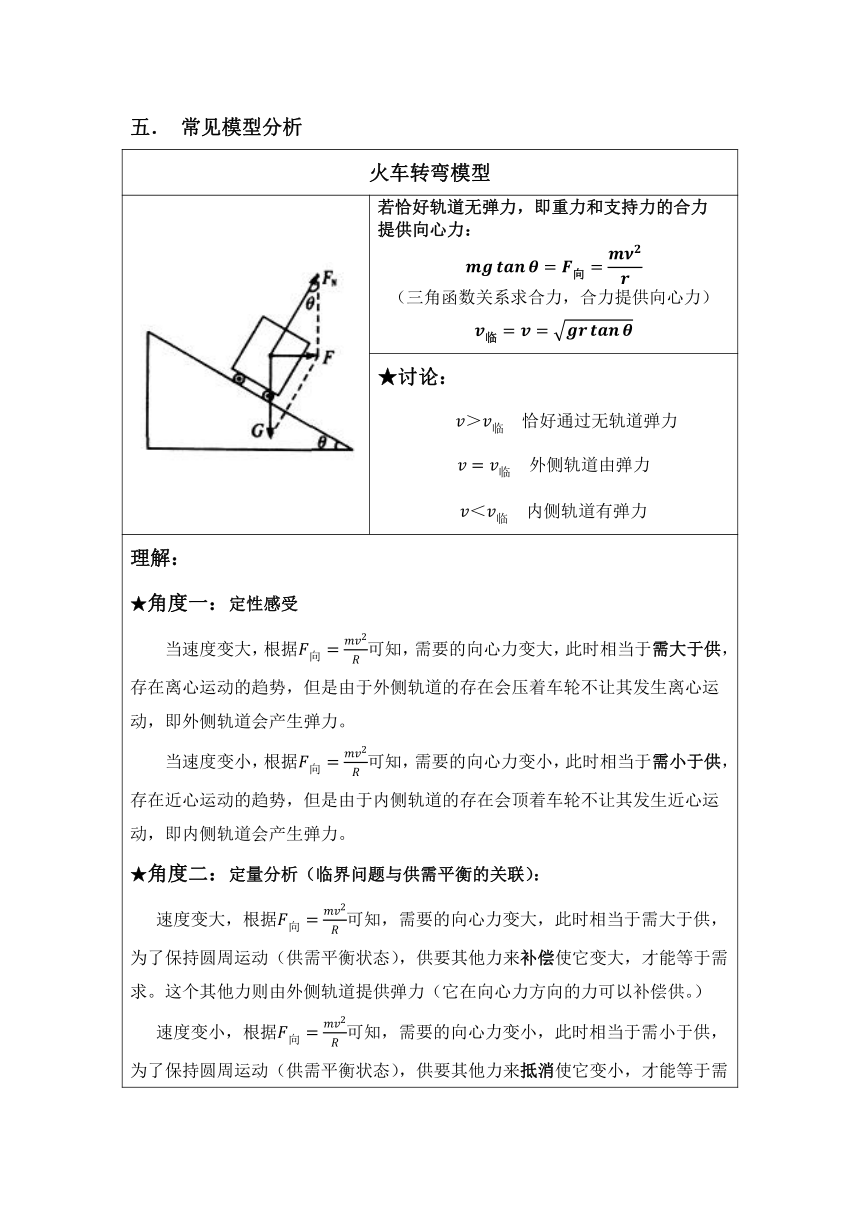
第六章 圆周运动知识点小结
一.基本物理量之间的关系:
注意:a与r即成反比,正比是因为它为定义式。
二. 传动 同轴转动模型
传动模型 同轴模型
特点 特点
注:齿轮模型等同于传动模型:齿数之比暗含半径之比。 应用: 1 定,定模型类别(注意特点) 2 找 找公式(包含已知量求解量的公式) 3 比 用已知量表示求解量,求比值
三. 物理概念
向心力 向心加速度:
始终指向圆心的力,根据效果命名为向心力(效果力) 始终指向圆心的加速度。(与向心力方向一致)
★特点:始终指向圆心,变力(方向时刻改变) ★作用效果:仅改变线速度方向,不改变大小 ★来源:由合力,分力,某个力提供 ★物理意义:描述线速度方向变化快慢的物理量 ★变加速度(方向时刻改变) (变加速=非匀=加速度改变)
圆周运动
匀速圆周运动 变速圆周运动
合力指向圆心,完全充当向心力 合力不指向圆心; 可分解为指向圆心的法向分力充当向心力,和沿着速度方向的切向分力使物体速度变化。
特点: 速度改变
注意: 一般的曲线运动,可在极短的位置处认为是圆弧的一部分,看做圆周运动来处理。
向心力实验
实验一:向心力演示仪
★注意一: 23为变速轮,为传动模型。即线速度相同,角速度之比为半径之比。而24,35为同轴转动模型,即对应角速度相同。所以23角速度之比即45角速度之比。 综上分析:变速轮的半径之比暗含小球转动角速度之比。 (变速轮半径)(球角速度) ★注意二: 控制变量法: 球质量,转动半径,转动角速度(改变变速轮半径)
五. 常见模型分析
火车转弯模型
若恰好轨道无弹力,即重力和支持力的合力 提供向心力: (三角函数关系求合力,合力提供向心力)
★讨论: 恰好通过无轨道弹力 外侧轨道由弹力 内侧轨道有弹力
理解: ★角度一:定性感受 当速度变大,根据可知,需要的向心力变大,此时相当于需大于供,存在离心运动的趋势,但是由于外侧轨道的存在会压着车轮不让其发生离心运动,即外侧轨道会产生弹力。 当速度变小,根据可知,需要的向心力变小,此时相当于需小于供,存在近心运动的趋势,但是由于内侧轨道的存在会顶着车轮不让其发生近心运动,即内侧轨道会产生弹力。 ★角度二:定量分析(临界问题与供需平衡的关联): 速度变大,根据可知,需要的向心力变大,此时相当于需大于供,为了保持圆周运动(供需平衡状态),供要其他力来补偿使它变大,才能等于需求。这个其他力则由外侧轨道提供弹力(它在向心力方向的力可以补偿供。) 速度变小,根据可知,需要的向心力变小,此时相当于需小于供,为了保持圆周运动(供需平衡状态),供要其他力来抵消使它变小,才能等于需求。这个其他力则由内侧轨道提供弹力(它在向心力方向的力可以抵消供。)
★拓展: 临界值,即恰好无弹力,无摩擦力等情景 做圆周运动的物体,总是具有从供需不等过渡到供需相等趋势
桥模型
凸形模型 凹形模型
公式: 公式:
失重(a向下) 超重(a向上)
★凸形模型讨论: N=0时,重力完全提供向心力。即: (若最高点,对地面无压力,物体将做平抛运动,且落在整圆外侧)
航天器的完全失重
将物体在地球表面的运动模型看成凸形模型: 根据 发现速度v上升,变小。当速度足够大,支持力可以为O。 N=0时,重力完全提供向心力,即: (以此速度运动,恰好对地面无压力,由于重力在个位置始终指向圆心,所以物体将围绕地球做匀速圆周运动)
离心运动
概念: 物体做圆周运动时,所提供的力突然消失,或小于需要的向心力时,物体将做离心运动。 条件:<
供需关系下的运动现象:
< 离心运动
近心运动
= 匀速圆周运动
沿切线飞出(离心运动)
六. 两类模型问题
(1)绳球模型
★B点: ★A点: ★通过A点的最小速度: 分析:→=0→=0 即 (此时恰好=0)
★讨论: 无法通过最高点 恰好通过 F绳=0 能通过,F绳向下 ★定性感受:若v,离心运动,因为有绳子拉着所有不会离心。 ★定量理解:若v,需要向心力大,原本的合力不够,需要F绳来弥补缺少的力,才能达到供需平衡。
(2)杆球模型
★B点: ★A点:(假设杆对球拉力) ★通过A点的最小速度: 分析:→=0→=-mg(杆对球支持力mg) 即: ★恰好通过A点的速度: 分析:恰好通过→=0 (此时恰好F杆=0)
★讨论: 杆对球产生向上支持力 恰好通过,F杆=0 杆对球产生向下拉力 定性感受(离心近心运动),定量理解(供需平衡)。
计算应用
受力分析 一重力二弹三摩擦,合力提供向心力 运动分析 定轨迹,定圆心,定半径,定方向
★列式计算: 法1:三角函数公式求出合力→→→→适用两力 法2:牛二正交分解法(x,y,摩擦力公式)→→→→适用多力 ★注意:正交分解的坐标系建立x轴指向半径方向,y轴垂直于半径方向。
八. 极限思想/临界情况简介
极限问题 临界问题
指某个力达到最大/小值的情况。 一般涉及最大摩擦力,绳/杆最大拉力等,沿着半径方向的合力提供向心力。当“供”达到最大/小值时,意味着物体运动的v,w等物理量达到最值,即为极限情况。 指某个力恰好为0的情况 一般涉及摩擦力,绳/杆弹力恰好为0。
处理方法: 先分析受力情况, 再找到受力的极值。 处理方法: 先计算出临界值, 再对实际值与临界值关系讨论分析。
一.基本物理量之间的关系:
注意:a与r即成反比,正比是因为它为定义式。
二. 传动 同轴转动模型
传动模型 同轴模型
特点 特点
注:齿轮模型等同于传动模型:齿数之比暗含半径之比。 应用: 1 定,定模型类别(注意特点) 2 找 找公式(包含已知量求解量的公式) 3 比 用已知量表示求解量,求比值
三. 物理概念
向心力 向心加速度:
始终指向圆心的力,根据效果命名为向心力(效果力) 始终指向圆心的加速度。(与向心力方向一致)
★特点:始终指向圆心,变力(方向时刻改变) ★作用效果:仅改变线速度方向,不改变大小 ★来源:由合力,分力,某个力提供 ★物理意义:描述线速度方向变化快慢的物理量 ★变加速度(方向时刻改变) (变加速=非匀=加速度改变)
圆周运动
匀速圆周运动 变速圆周运动
合力指向圆心,完全充当向心力 合力不指向圆心; 可分解为指向圆心的法向分力充当向心力,和沿着速度方向的切向分力使物体速度变化。
特点: 速度改变
注意: 一般的曲线运动,可在极短的位置处认为是圆弧的一部分,看做圆周运动来处理。
向心力实验
实验一:向心力演示仪
★注意一: 23为变速轮,为传动模型。即线速度相同,角速度之比为半径之比。而24,35为同轴转动模型,即对应角速度相同。所以23角速度之比即45角速度之比。 综上分析:变速轮的半径之比暗含小球转动角速度之比。 (变速轮半径)(球角速度) ★注意二: 控制变量法: 球质量,转动半径,转动角速度(改变变速轮半径)
五. 常见模型分析
火车转弯模型
若恰好轨道无弹力,即重力和支持力的合力 提供向心力: (三角函数关系求合力,合力提供向心力)
★讨论: 恰好通过无轨道弹力 外侧轨道由弹力 内侧轨道有弹力
理解: ★角度一:定性感受 当速度变大,根据可知,需要的向心力变大,此时相当于需大于供,存在离心运动的趋势,但是由于外侧轨道的存在会压着车轮不让其发生离心运动,即外侧轨道会产生弹力。 当速度变小,根据可知,需要的向心力变小,此时相当于需小于供,存在近心运动的趋势,但是由于内侧轨道的存在会顶着车轮不让其发生近心运动,即内侧轨道会产生弹力。 ★角度二:定量分析(临界问题与供需平衡的关联): 速度变大,根据可知,需要的向心力变大,此时相当于需大于供,为了保持圆周运动(供需平衡状态),供要其他力来补偿使它变大,才能等于需求。这个其他力则由外侧轨道提供弹力(它在向心力方向的力可以补偿供。) 速度变小,根据可知,需要的向心力变小,此时相当于需小于供,为了保持圆周运动(供需平衡状态),供要其他力来抵消使它变小,才能等于需求。这个其他力则由内侧轨道提供弹力(它在向心力方向的力可以抵消供。)
★拓展: 临界值,即恰好无弹力,无摩擦力等情景 做圆周运动的物体,总是具有从供需不等过渡到供需相等趋势
桥模型
凸形模型 凹形模型
公式: 公式:
失重(a向下) 超重(a向上)
★凸形模型讨论: N=0时,重力完全提供向心力。即: (若最高点,对地面无压力,物体将做平抛运动,且落在整圆外侧)
航天器的完全失重
将物体在地球表面的运动模型看成凸形模型: 根据 发现速度v上升,变小。当速度足够大,支持力可以为O。 N=0时,重力完全提供向心力,即: (以此速度运动,恰好对地面无压力,由于重力在个位置始终指向圆心,所以物体将围绕地球做匀速圆周运动)
离心运动
概念: 物体做圆周运动时,所提供的力突然消失,或小于需要的向心力时,物体将做离心运动。 条件:<
供需关系下的运动现象:
< 离心运动
近心运动
= 匀速圆周运动
沿切线飞出(离心运动)
六. 两类模型问题
(1)绳球模型
★B点: ★A点: ★通过A点的最小速度: 分析:→=0→=0 即 (此时恰好=0)
★讨论: 无法通过最高点 恰好通过 F绳=0 能通过,F绳向下 ★定性感受:若v,离心运动,因为有绳子拉着所有不会离心。 ★定量理解:若v,需要向心力大,原本的合力不够,需要F绳来弥补缺少的力,才能达到供需平衡。
(2)杆球模型
★B点: ★A点:(假设杆对球拉力) ★通过A点的最小速度: 分析:→=0→=-mg(杆对球支持力mg) 即: ★恰好通过A点的速度: 分析:恰好通过→=0 (此时恰好F杆=0)
★讨论: 杆对球产生向上支持力 恰好通过,F杆=0 杆对球产生向下拉力 定性感受(离心近心运动),定量理解(供需平衡)。
计算应用
受力分析 一重力二弹三摩擦,合力提供向心力 运动分析 定轨迹,定圆心,定半径,定方向
★列式计算: 法1:三角函数公式求出合力→→→→适用两力 法2:牛二正交分解法(x,y,摩擦力公式)→→→→适用多力 ★注意:正交分解的坐标系建立x轴指向半径方向,y轴垂直于半径方向。
八. 极限思想/临界情况简介
极限问题 临界问题
指某个力达到最大/小值的情况。 一般涉及最大摩擦力,绳/杆最大拉力等,沿着半径方向的合力提供向心力。当“供”达到最大/小值时,意味着物体运动的v,w等物理量达到最值,即为极限情况。 指某个力恰好为0的情况 一般涉及摩擦力,绳/杆弹力恰好为0。
处理方法: 先分析受力情况, 再找到受力的极值。 处理方法: 先计算出临界值, 再对实际值与临界值关系讨论分析。
