苏科版 七年级下册 12.3互逆命题 课件(共15张PPT)
文档属性
| 名称 | 苏科版 七年级下册 12.3互逆命题 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 86.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-25 19:58:44 | ||
图片预览





文档简介
(共15张PPT)
初 一 数 学
12.3 互逆命题
一般地,对某一件事情作出判断的句子叫做命题 .
命题由条件和结论两部分组成.
1.什么叫命题
2.命题由哪两部分组成
【温故知新】
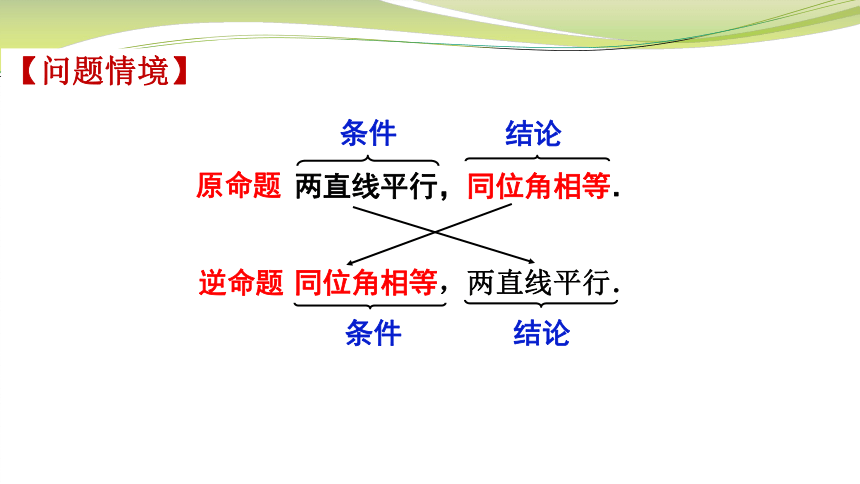
两直线平行,同位角相等.
条件
结论
同位角相等,两直线平行.
条件
结论
【问题情境】
原命题
逆命题
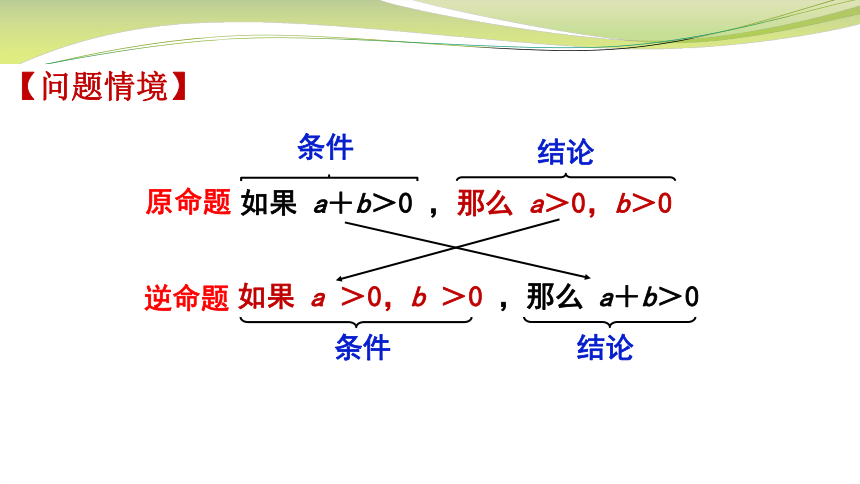
如果 a+b>0 ,那么 a>0,b>0
如果 a >0,b >0 ,那么 a+b>0
【问题情境】
条件
结论
条件
结论
原命题
逆命题
两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.
其中一个命题是另一个命题的逆命题.
【明确概念】
1.在下列命题中,哪些是互逆命题?
①直角都相等;
②内错角相等,两直线平行;
③如果a+b>0, 那么a>0,b>0;
④相等的角都是直角;
⑤如果a>0,b>0, 那么ab>0;
⑥两直线平行,内错角相等。
【尝试练习】
1.在下列命题中,哪些是互逆命题?
①直角都相等;
④相等的角都是直角;
②内错角相等,两直线平行;
⑥两直线平行,内错角相等。
【尝试练习】
把原命题的条件和结论互换就可以得到它的逆命题.
任何一个数学命题都有逆命题.
【明确概念】
(4)锐角与钝角互为补角.
逆命题:如果a=b,那么a2=b2 .
逆命题:如果两个角的平分线组成一个平角,那么这两个角是对顶角.
逆命题:能被5整除的数的末位数字是5.
逆命题:互为补角的两个角一个是锐角一个是钝角.
例1.指出下列命题的逆命题,并判断原命题和逆命题的真假性.
(1)如果a2=b2,那么a=b;
(2)如果两个角是对顶角,那么它们的平分线组成一个平角;
(3)末位数字是5的数,能被5整除;
【例题赏析】
假命题
真命题
真命题
真命题
真命题
假命题
假命题
假命题
例2.判断下列命题的真假性,并说明理由.
假命题
如:锐角300与钝角1000,而它们不是互为补角.
感悟:判断一个命题是假命题,只需举一个具体的反例.
像这样,举出一个具体例子来说明一个命题是假命题,这样的例子称为反例。
【例题赏析】
(1)如果 a2>0,那么a>0
(2)锐角与钝角互为补角
如:a=-5,(-5)2=25>0,而-5<0.
假命题
2. 举反例说明下列命题是假命题.
反例:a=10,b=-5,a+b>0,a>0,b<0.
)
)
反例:锐角400、750的和是钝角.
2
1
反例:如图,∠1与∠2是同位角,但不相等.
【尝试练习】
(3)两个锐角的和是直角
(2) 同位角一定相等.
(1)如果a+b>0,那么a>0,b>0;
【随堂检测】
1.下列各组命题是否是互逆命题:
(4)“同位角相等,两直线平行”与“同位角不相等,两直线不平行” .
(3)“对顶角相等”与“如果两个角相等,那么这两个角是对顶角”;
(2)“平面内,垂直于同一条直线的两条直线互相平行”与“如果平面内两两条直线都垂直于第三条直线,那么这两条直线互相平行”;
(1)“正方形的四个角都是直角”与“四个角都是直角的四边形是正方形”;
是互逆命题
不是互逆命题,是同一个命题
是互逆命题
不是互逆命题
(1)“两直线平行,内错角相等”的逆命题是
____________________________.
(2) 命题“对顶角相等”的逆命题是
___________________,这个逆命题是____命题.
(3) 请写出一个原命题是真命题,逆命题是假命题的命题:
_____________________ _______________________
内错角相等,两直线平行.
相等的角是对顶角
假
原命题:直角都相等.
逆命题:相等的角是直角.
2.填空题:
【随堂检测】
3.举反例说明下列命题是假命题:
【随堂检测】
(4)如果一点到线段两端的距离相等,那么这点是这条线段的中点.
(3)两个锐角的和是钝角;
(2)任何一个数的平方都大于0;
(1)如果|a|=|b| ,那么a=b;
反例:a=5,b=-5,|5|=|-5|,但5≠-5.
反例:02 = 0.
反例:锐角400与200的和是600,是锐角.
反例:如图,PA=PB,显然点P不是线段AB中点.
1、互为逆命题:会写出一个命题的逆命题;
【小结感悟】
3、假命题的证明:会举反例.
2、命题真假性:能判断真假命题;
初 一 数 学
12.3 互逆命题
一般地,对某一件事情作出判断的句子叫做命题 .
命题由条件和结论两部分组成.
1.什么叫命题
2.命题由哪两部分组成
【温故知新】
两直线平行,同位角相等.
条件
结论
同位角相等,两直线平行.
条件
结论
【问题情境】
原命题
逆命题
如果 a+b>0 ,那么 a>0,b>0
如果 a >0,b >0 ,那么 a+b>0
【问题情境】
条件
结论
条件
结论
原命题
逆命题
两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.
其中一个命题是另一个命题的逆命题.
【明确概念】
1.在下列命题中,哪些是互逆命题?
①直角都相等;
②内错角相等,两直线平行;
③如果a+b>0, 那么a>0,b>0;
④相等的角都是直角;
⑤如果a>0,b>0, 那么ab>0;
⑥两直线平行,内错角相等。
【尝试练习】
1.在下列命题中,哪些是互逆命题?
①直角都相等;
④相等的角都是直角;
②内错角相等,两直线平行;
⑥两直线平行,内错角相等。
【尝试练习】
把原命题的条件和结论互换就可以得到它的逆命题.
任何一个数学命题都有逆命题.
【明确概念】
(4)锐角与钝角互为补角.
逆命题:如果a=b,那么a2=b2 .
逆命题:如果两个角的平分线组成一个平角,那么这两个角是对顶角.
逆命题:能被5整除的数的末位数字是5.
逆命题:互为补角的两个角一个是锐角一个是钝角.
例1.指出下列命题的逆命题,并判断原命题和逆命题的真假性.
(1)如果a2=b2,那么a=b;
(2)如果两个角是对顶角,那么它们的平分线组成一个平角;
(3)末位数字是5的数,能被5整除;
【例题赏析】
假命题
真命题
真命题
真命题
真命题
假命题
假命题
假命题
例2.判断下列命题的真假性,并说明理由.
假命题
如:锐角300与钝角1000,而它们不是互为补角.
感悟:判断一个命题是假命题,只需举一个具体的反例.
像这样,举出一个具体例子来说明一个命题是假命题,这样的例子称为反例。
【例题赏析】
(1)如果 a2>0,那么a>0
(2)锐角与钝角互为补角
如:a=-5,(-5)2=25>0,而-5<0.
假命题
2. 举反例说明下列命题是假命题.
反例:a=10,b=-5,a+b>0,a>0,b<0.
)
)
反例:锐角400、750的和是钝角.
2
1
反例:如图,∠1与∠2是同位角,但不相等.
【尝试练习】
(3)两个锐角的和是直角
(2) 同位角一定相等.
(1)如果a+b>0,那么a>0,b>0;
【随堂检测】
1.下列各组命题是否是互逆命题:
(4)“同位角相等,两直线平行”与“同位角不相等,两直线不平行” .
(3)“对顶角相等”与“如果两个角相等,那么这两个角是对顶角”;
(2)“平面内,垂直于同一条直线的两条直线互相平行”与“如果平面内两两条直线都垂直于第三条直线,那么这两条直线互相平行”;
(1)“正方形的四个角都是直角”与“四个角都是直角的四边形是正方形”;
是互逆命题
不是互逆命题,是同一个命题
是互逆命题
不是互逆命题
(1)“两直线平行,内错角相等”的逆命题是
____________________________.
(2) 命题“对顶角相等”的逆命题是
___________________,这个逆命题是____命题.
(3) 请写出一个原命题是真命题,逆命题是假命题的命题:
_____________________ _______________________
内错角相等,两直线平行.
相等的角是对顶角
假
原命题:直角都相等.
逆命题:相等的角是直角.
2.填空题:
【随堂检测】
3.举反例说明下列命题是假命题:
【随堂检测】
(4)如果一点到线段两端的距离相等,那么这点是这条线段的中点.
(3)两个锐角的和是钝角;
(2)任何一个数的平方都大于0;
(1)如果|a|=|b| ,那么a=b;
反例:a=5,b=-5,|5|=|-5|,但5≠-5.
反例:02 = 0.
反例:锐角400与200的和是600,是锐角.
反例:如图,PA=PB,显然点P不是线段AB中点.
1、互为逆命题:会写出一个命题的逆命题;
【小结感悟】
3、假命题的证明:会举反例.
2、命题真假性:能判断真假命题;
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
