苏科版七年级下册12.2证明课件(共20张PPT)
文档属性
| 名称 | 苏科版七年级下册12.2证明课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-25 20:27:44 | ||
图片预览





文档简介
(共20张PPT)
12.2证明(3)
数学来源于生活
生活中有很多事情都是先知道结论,然后再去慢慢探究为什么?(如苹果熟了自然会从树上掉下来,牛顿就问为什么?)
数学来源于生活
(又如人们在游泳时会漂浮在水面上,阿基米德就问为什么?)
为什么?
1800
三角形内角和是
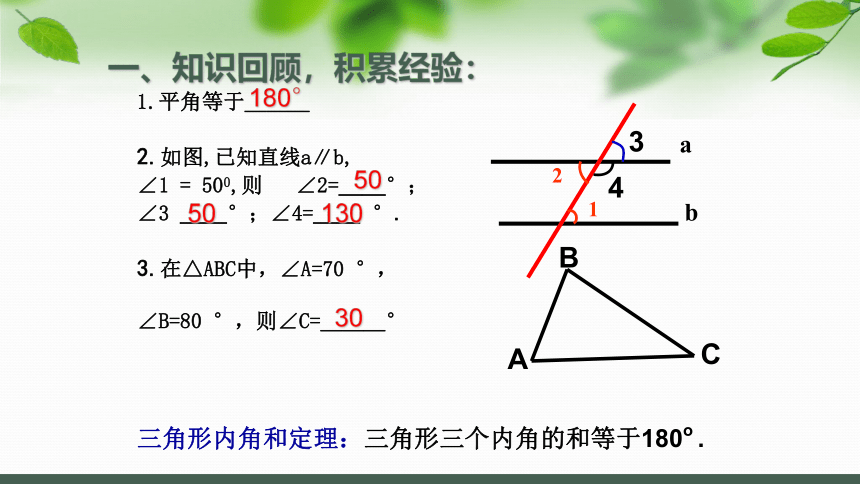
一、知识回顾,积累经验:
1.平角等于___
2.如图,已知直线a∥b,
∠1 = 500,则 ∠2=__°;
∠3 __°;∠4=__ °.
3.在△ABC中,∠A=70 °,
∠B=80 °,则∠C=___°
180°
a
b
1
2
3
4
B
C
A
三角形内角和定理:三角形三个内角的和等于180o .
50
50
130
30
二、情景再现,引入新课:
三角形内角和定理:三角形三个内角的和等于180o .
问题1:你有哪些方法验证三角形三个内角的和等于180o
(1) 测量法(量角器)
问题2:通过你的验证能说明所有三角形的内角和都 等于180°吗?为什么?
(2)拼图法(平角)
问题3:全班同学的验证结果能说明所有三角形的内角和
都等于180°吗?
问题4:那么怎样才能说明“三角形内角和是180°”呢?
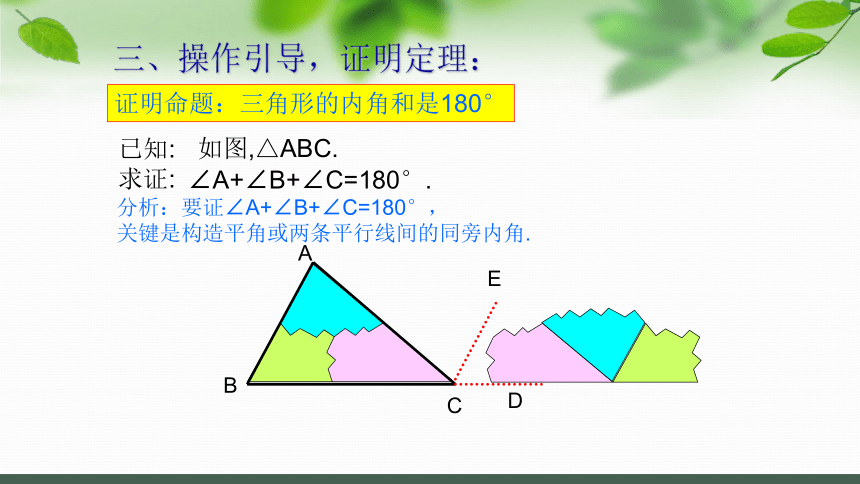
证明命题:三角形的内角和是180°
已知:
求证:
如图,△ABC.
∠A+∠B+∠C=180°.
分析:要证∠A+∠B+∠C=180°,
关键是构造平角或两条平行线间的同旁内角.
三、操作引导,证明定理:
A
B
C
D
E
关于辅助线:
辅助线是为了证明需要在原图上添画的线.(辅助线通常画成虚线)
它的作用是把分散的条件集中,把隐含的条件显现出来,起到牵线搭桥的作用.
添加辅助线,可构造新图形,形成新关系,找到联系已知与未知的桥梁,把问题转化,但辅助线的添法没有一定的规律,要根据需要而定,平时做题时要注意总结.
D
E
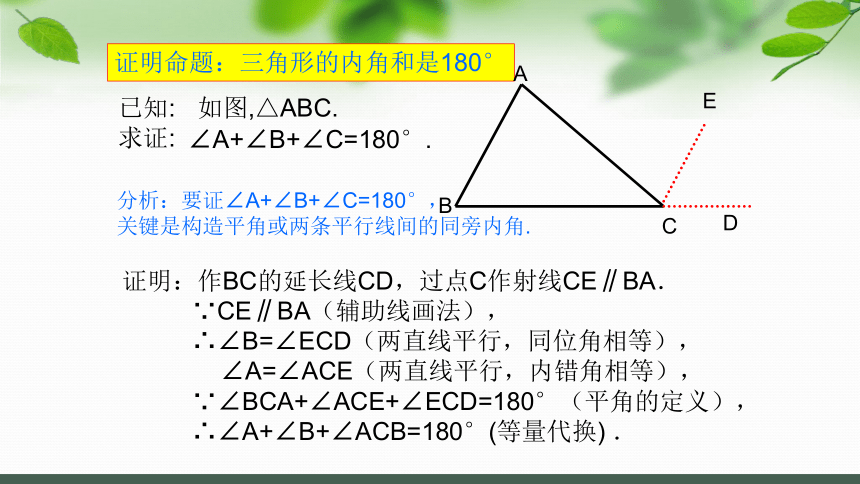
证明命题:三角形的内角和是180°
已知:
求证:
如图,△ABC.
∠A+∠B+∠C=180°.
分析:要证∠A+∠B+∠C=180°,
关键是构造平角或两条平行线间的同旁内角.
A
B
C
证明:作BC的延长线CD,过点C作射线CE∥BA.
∵CE∥BA(辅助线画法),
∴∠B=∠ECD(两直线平行,同位角相等),
∠A=∠ACE(两直线平行,内错角相等),
∵∠BCA+∠ACE+∠ECD=180°(平角的定义),
∴∠A+∠B+∠ACB=180°(等量代换) .
已知:
求证:
如图,△ABC.
∠A+∠B+∠C=180°.
证明命题:三角形的内角和是180°
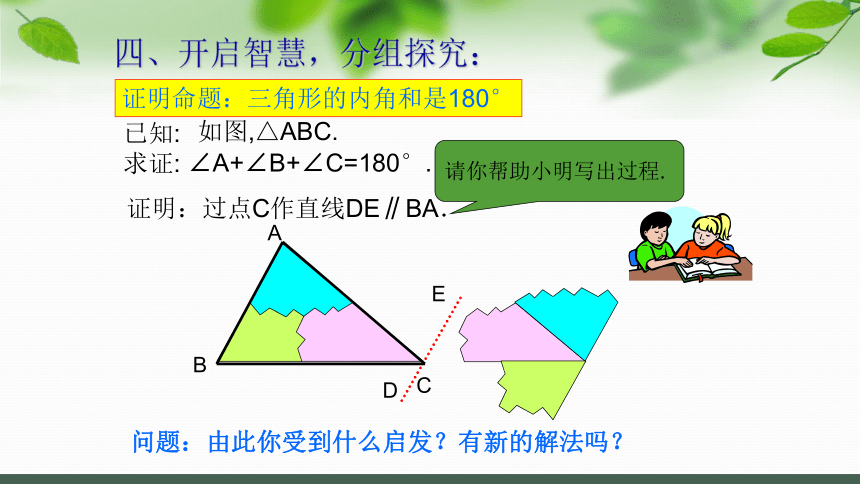
四、开启智慧,分组探究:
A
B
C
D
E
证明:过点C作直线DE∥BA.
请你帮助小明写出过程.
问题:由此你受到什么启发?有新的解法吗?
已知:
求证:
如图,△ABC.
∠A+∠B+∠C=180°.
证明命题:三角形的内角和是180°
一题多解,分组讨论:
A
B
C
.
思考:添加的这些辅助线有什么相同点和不同点?
不同点:取点不同;
相同点:过点作三边的平行线.
思路总结
为了说明三个角的和为1800,转化为一个平角或两直线平行的同旁内角互补,体现了数学中的转化思想;
为了证明的需要在原图上添加的辅助线的可构造新图形,形成新关系,找到联系已知与未知的桥梁,把新问题转化为我们已经会解决的问题,又体现了我们数学中的转化思想。
三角形内角和定理
三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.
这里的结论,以后可以直接运用.
A
B
C
“因”
“果”
“依据”
五、实践应用,培养能力:
议一议:三角形的一个外角与它不相邻的两个内角
有怎样的数量关系?
A
B
C
D
E
已知:∠ACD是△ABC的一个外角.
求证:∠ACD=∠A+∠B.
想一想:还有其它解法吗?
在△ABC中,
∠A+∠B+∠ACB= 180o (三角形的内角和等于180o ).
∴∠A+∠B =180°-∠ACB(等式性质).
∵∠ACB+∠ACD=180°(平角的定义),
∴∠ACD =180°-∠ACB(等式性质).
∴∠ACD=∠ A+∠B (等量代换).
证明:
三角形的外角等于与它不相邻的两个内角的和.
例题教学:
例2 已知:如图,AC、BD相交于点O.
求证:∠A+∠B=∠C+∠D.
在△AOB中,
∠A+∠B+∠AOB= 180o (三角形的内角和等于180o ).
∴∠A+∠B =180°-∠AOB(等式性质).
在△AOB中,同理得:∠C+∠D =180°-∠COD.
∵∠AOB=∠COD(对顶角相等).
∴∠A+∠B=∠C+∠D(等量代换).
证明:
B
A
C
D
O
变式训练
A
B
C
D
O
E
求∠A+∠B+∠C+∠D+∠E的度数.
1
(
2
(
已知:如图,AC、BD相交于点O,
求证:∠A+∠B=∠C+∠D.
例题
已知:如图,在△ABC中,DE∥BC,∠A=60°,
∠C=70°.
求证: ∠ADE=50°
随堂练习
相信你能行!
已知:如图,AD是△ABC的角平分线,E是BC
求证:∠ADE=∠DAE.
相信你能行!
延长线上一点,∠EAC=∠B.
随堂练习
(
(
(
(
1
2
六、畅谈收获,反思升华:
通过今天的学习,你有何收获和体会.把你的收获告诉你的同学。
知识树
三角形的内角和定理
推论
不同的证明方法
辅助线的作法、作用
转化角的方法
转化思想
12.2证明(3)
数学来源于生活
生活中有很多事情都是先知道结论,然后再去慢慢探究为什么?(如苹果熟了自然会从树上掉下来,牛顿就问为什么?)
数学来源于生活
(又如人们在游泳时会漂浮在水面上,阿基米德就问为什么?)
为什么?
1800
三角形内角和是
一、知识回顾,积累经验:
1.平角等于___
2.如图,已知直线a∥b,
∠1 = 500,则 ∠2=__°;
∠3 __°;∠4=__ °.
3.在△ABC中,∠A=70 °,
∠B=80 °,则∠C=___°
180°
a
b
1
2
3
4
B
C
A
三角形内角和定理:三角形三个内角的和等于180o .
50
50
130
30
二、情景再现,引入新课:
三角形内角和定理:三角形三个内角的和等于180o .
问题1:你有哪些方法验证三角形三个内角的和等于180o
(1) 测量法(量角器)
问题2:通过你的验证能说明所有三角形的内角和都 等于180°吗?为什么?
(2)拼图法(平角)
问题3:全班同学的验证结果能说明所有三角形的内角和
都等于180°吗?
问题4:那么怎样才能说明“三角形内角和是180°”呢?
证明命题:三角形的内角和是180°
已知:
求证:
如图,△ABC.
∠A+∠B+∠C=180°.
分析:要证∠A+∠B+∠C=180°,
关键是构造平角或两条平行线间的同旁内角.
三、操作引导,证明定理:
A
B
C
D
E
关于辅助线:
辅助线是为了证明需要在原图上添画的线.(辅助线通常画成虚线)
它的作用是把分散的条件集中,把隐含的条件显现出来,起到牵线搭桥的作用.
添加辅助线,可构造新图形,形成新关系,找到联系已知与未知的桥梁,把问题转化,但辅助线的添法没有一定的规律,要根据需要而定,平时做题时要注意总结.
D
E
证明命题:三角形的内角和是180°
已知:
求证:
如图,△ABC.
∠A+∠B+∠C=180°.
分析:要证∠A+∠B+∠C=180°,
关键是构造平角或两条平行线间的同旁内角.
A
B
C
证明:作BC的延长线CD,过点C作射线CE∥BA.
∵CE∥BA(辅助线画法),
∴∠B=∠ECD(两直线平行,同位角相等),
∠A=∠ACE(两直线平行,内错角相等),
∵∠BCA+∠ACE+∠ECD=180°(平角的定义),
∴∠A+∠B+∠ACB=180°(等量代换) .
已知:
求证:
如图,△ABC.
∠A+∠B+∠C=180°.
证明命题:三角形的内角和是180°
四、开启智慧,分组探究:
A
B
C
D
E
证明:过点C作直线DE∥BA.
请你帮助小明写出过程.
问题:由此你受到什么启发?有新的解法吗?
已知:
求证:
如图,△ABC.
∠A+∠B+∠C=180°.
证明命题:三角形的内角和是180°
一题多解,分组讨论:
A
B
C
.
思考:添加的这些辅助线有什么相同点和不同点?
不同点:取点不同;
相同点:过点作三边的平行线.
思路总结
为了说明三个角的和为1800,转化为一个平角或两直线平行的同旁内角互补,体现了数学中的转化思想;
为了证明的需要在原图上添加的辅助线的可构造新图形,形成新关系,找到联系已知与未知的桥梁,把新问题转化为我们已经会解决的问题,又体现了我们数学中的转化思想。
三角形内角和定理
三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.
这里的结论,以后可以直接运用.
A
B
C
“因”
“果”
“依据”
五、实践应用,培养能力:
议一议:三角形的一个外角与它不相邻的两个内角
有怎样的数量关系?
A
B
C
D
E
已知:∠ACD是△ABC的一个外角.
求证:∠ACD=∠A+∠B.
想一想:还有其它解法吗?
在△ABC中,
∠A+∠B+∠ACB= 180o (三角形的内角和等于180o ).
∴∠A+∠B =180°-∠ACB(等式性质).
∵∠ACB+∠ACD=180°(平角的定义),
∴∠ACD =180°-∠ACB(等式性质).
∴∠ACD=∠ A+∠B (等量代换).
证明:
三角形的外角等于与它不相邻的两个内角的和.
例题教学:
例2 已知:如图,AC、BD相交于点O.
求证:∠A+∠B=∠C+∠D.
在△AOB中,
∠A+∠B+∠AOB= 180o (三角形的内角和等于180o ).
∴∠A+∠B =180°-∠AOB(等式性质).
在△AOB中,同理得:∠C+∠D =180°-∠COD.
∵∠AOB=∠COD(对顶角相等).
∴∠A+∠B=∠C+∠D(等量代换).
证明:
B
A
C
D
O
变式训练
A
B
C
D
O
E
求∠A+∠B+∠C+∠D+∠E的度数.
1
(
2
(
已知:如图,AC、BD相交于点O,
求证:∠A+∠B=∠C+∠D.
例题
已知:如图,在△ABC中,DE∥BC,∠A=60°,
∠C=70°.
求证: ∠ADE=50°
随堂练习
相信你能行!
已知:如图,AD是△ABC的角平分线,E是BC
求证:∠ADE=∠DAE.
相信你能行!
延长线上一点,∠EAC=∠B.
随堂练习
(
(
(
(
1
2
六、畅谈收获,反思升华:
通过今天的学习,你有何收获和体会.把你的收获告诉你的同学。
知识树
三角形的内角和定理
推论
不同的证明方法
辅助线的作法、作用
转化角的方法
转化思想
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
