苏科版七年级下册11.5用一元一次不等式解决问题复习课件(共17张PPT)
文档属性
| 名称 | 苏科版七年级下册11.5用一元一次不等式解决问题复习课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 814.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-25 20:47:23 | ||
图片预览






文档简介
(共17张PPT)
用一元一次不等式解决问题复习
【要点梳理】
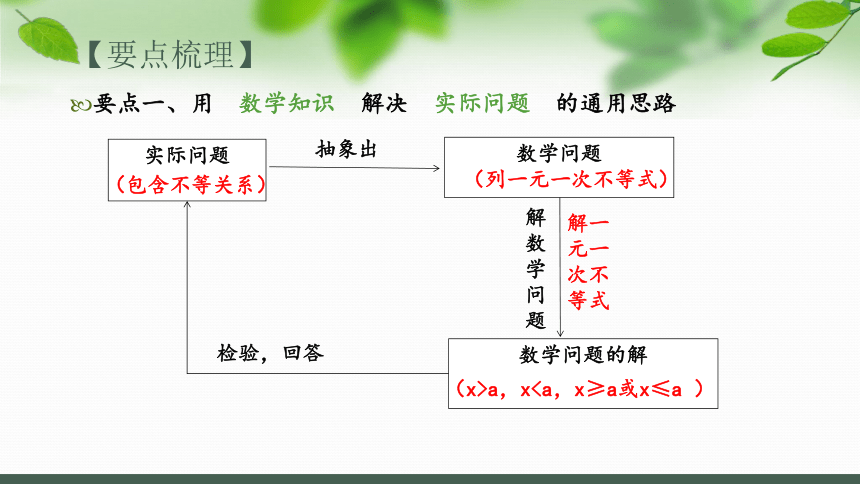
要点一、用 数学知识 解决 实际问题 的通用思路
实际问题
数学问题
数学问题的解
检验,回答
(包含不等关系)
(列一元一次不等式)
(x>a,x抽象出
解数学问题
解一元一次不等式
【要点梳理】
要点二、列不等式解决实际问题的步骤
列一元一次不等式解决实际问题与列一元一次方程、二元一次方程组解决实际问题类似,通常也需要经过以下几个步骤:
(1)审:认真审题,分清已知量、未知量及其关系,找出题中不等关系要抓住题中的关键字眼,如“大于”、“小于”、“不大于”、“至少”、“超过”、“不超过”等;
(2)设:设出适当的未知数。在设未知数时,表示不等关系的文字如“至少”“最多”等不能出现,即应给出肯定的未知数的设法;
(3)列:根据题中的不等关系,列出不等式;
(4)解:解所列的不等式;
(5)验:检验求得的解集是否正确、是否符合实际意义;
(6)答:写出答案,把表示不等关系的文字补上。
【基础练习】
1.某汽车厂改进生产工艺后,每天生产的汽车比原来每天生产的汽车多6辆,那么现在15天的产量就超过了原来20天的产量,设原来每天生产汽车x辆,则列出的不等式为( )
A.15x>20(x+6) B.15(x+6)>20x C.15x>20(x-6) D.15(x-6)>20x
【解析】 由题意得:15(x+6)>20x
B
2.喜迎建党100周年,某校举行党史知识竞赛,共30道题,每道题都给出4个答案,其中只有一个答案正确,选对得4分,不选或选错扣2分,得分不低于80分得奖,那么得奖至少应选对的题数是( )
A.23 B.24 C.25 D.26
B
【解析】设选对x道题,则不选或选错(30﹣x)道题,
依题意,得:4x﹣2(30﹣x)≥80,
解得: .
∵x为正整数,
∴要得奖至少应选对24道题
【基础练习】
3.某种商品的进价为500元,出售时标价为750元,由于换季,商店准备打折销售,但要保持利润不低于20%,那么至多打( )
A.6折 B.7折 C.8折 D.9折
C
【解析】设该商品打x折销售,
依题意得: ,
解得:x≥8.
【基础练习】
4.“垃圾分类做得好,明天生活会更好”,学校需要购买分类垃圾桶10个,放在校园的公共区域,市场上有A型和B型两种分类垃圾桶,A型分类垃圾桶350元/个,B型分类垃圾桶400元/个,总费用不超过3650元,则不同的购买方式有( )
A.2种 B.3种 C.4种 D.5种
【解析】设购买A型分类垃圾桶x个,则购买B型分类垃圾桶(10﹣x)个
依题意,得:350x+400(10﹣x)≤3650,
解得:x≥7.
∵x,(10﹣x)均为非负整数,
∴x可以为7,8,9,10,
∴共有4种购买方案.
C
【基础练习】
计算提醒:先同除以50,再去括号计算
7x+8(10-x)≤73
5.某种型号汽车每行驶100km耗油10L,其油箱容量为40L.为了有效延长汽车使用寿命,厂家建议每次加油时油箱内剩余油量不低于油箱容量的 ,按此建议,一辆加满油的该型号汽车最多行驶的路程是 _____ km.
350
【解析】设行驶xkm,
∵油箱内剩余油量不低于油箱容量的,
∴ .
∴x≤350
故该辆汽车最多行驶的路程是350km。
【基础练习】
6.小明受《乌鸦喝水》故事的启发,利用量筒和体积相同的小球进行了如下操作,请根据图中给出的信息,量筒中至少放入 个小球时有水溢出.
11
不等关系:原来水的高度+放入x个小球后水上升的高度>量筒的高度
【解析】由题意可得每添加一个球,水面上升 cm
设放入x个小球时有水溢出,则
解得
即至少放入11个小球时有水溢出.
【基础练习】
【典型例题】类型一、营销问题
例1.(2020春 常州期末)2020年初,由于新冠病毒的蔓延,口罩市场出现热销,小明的爸爸用18000元购进甲、乙两种型号的口罩,在自家药店销售,销售完后共获利3900元,进价和售价如表所示:
价格型号 甲种型号口罩 乙种型号口罩
进价(元/袋) 20 30
售价(元/袋) 25 36
(1)小明爸爸的药店购进甲、乙两种型号的口罩各多少袋?
解:(1)设小明爸爸的商店购进甲种型号口罩x袋,乙种型号口罩y袋,
根据题意得,
解得:
答:小明爸爸的药店购进甲种型号口罩300袋,乙种型号口罩400袋;
例1.(2020春 常州期末)2020年初,由于新冠病毒的蔓延,口罩市场出现热销,小明的爸爸用18000元购进甲、乙两种型号的口罩,在自家药店销售,销售完后共获利3900元,进价和售价如表所示:
价格型号 甲种型号口罩 乙种型号口罩
进价(元/袋) 20 30
售价(元/袋) 25 36
(2)设需购进a袋乙种型号的口罩,则需购进甲种型号的口罩(800-a)袋
根据题意得,(25﹣20)(800﹣a)+(36﹣30)a≥4500.
解这个不等式,得a≥500.
答:至少需购进500袋乙种型号的口罩.
(2)由于需求量大,口罩很快售完,小明的爸爸决定再一次购进甲、乙两种型号的口罩共800袋.如果要使这800袋口罩全部售完后所得利润不低于4500元,那么至少需购进多少袋乙种型号的口罩?
【典型例题】类型一、营销问题
例2.计划对河道进行改造,现有甲乙两个工程队参加改造施工,受条件限制,每天只能由一个工程队施工.若甲工程队先单独施工3天,再由乙工程队单独施工5天,则可以完成550米施工任务;若甲工程队先单独施工2天,再由乙工程对单独施工4天,则可以完成420米的施工任务.
(1)求甲、乙两个工程队平均每天分别能完成多少米施工任务?
(2)该河道全长6000米,若两队合作工期不能超过90天,乙工程队至少施工多少天?
解:(1)设甲工程队平均每天施工x米,
乙工程队平均每天施工y米,
根据题意得:
解得:
答:甲工程队平均每天能完成施工任务50米,
乙工程队平均每天能完成施工任务80米.
(2)设乙工程队施工a天,
则甲工程队施工(90-a)天
根据题意得:50(90-a)+80a≥6000,
解得:a≥50,
答:乙工程队至少施工50天.
【典型例题】类型二、工程问题
如果工作90天,完成的河道应不少于6000米
例3.联通公司推出两种手机收费方案.方案一:月租费36元,本地通话话费0.1元/分;方案二:不收月租费,本地通话费为0.6元/分.设小明的爸爸一个月通话时间为x分钟.小明爸爸选择哪种方案才合算呢?
解:
由题意得,方案一需付费(36+0.1x)元,
方案二需付费0.6x元。
∴当36+0.1x<0.6x,即x>72时,方案一比方案二优惠,此时小明爸爸选择方案一合算;
当36+0.1x=0.6x,即x=72时,两种方案费用相同,小明爸爸均可选择;
当36+0.1x>0.6x,即x<72时,方案二比方案一优惠,此时小明爸爸选择方案二合算。
【典型例题】类型三、方案选择
例4.为了让市民树立起“珍惜水、节约水、保护水”的用水理念,居民生活用水按阶梯式计算水价,水价计算方式如表所示,每吨水还需另加污水处理费0.60元.已知小明家今年1月份用水20吨,交水费60元;2月份用水25吨,交水费79元.(友情提示:水费=水价+污水处理费)
(1)求m,n的值.
解:(1)由题意得
解得
答:m的值为2.4,n的值为3.2。
(2)2%×11650=233(元),
由(1)得m=2.4,n=3.2,
当用水量为30吨时,水费为:20×2.4+10×3.2+30×0.6=98(元),
∵233>98,∴小明家3月份用水量超过30吨.
可设小明家3月份用水x吨,
由题意得20×2.4+10×3.2+2×2.4(x﹣30)+0.6x≤233
或98+(2×2.4+0.6)(x﹣30)≤233,
解得x≤55,答:小明家3月份最多能用水55吨.
【典型例题】类型四、分段收费
用水量 水价(元/吨)
不超过20吨 m
超过20吨且不超过30吨的部分 n
超过30吨的部分 2m
(2)为了节省开支,小明计划把3月份的水费控制在不超过家庭月收入的2%.若小明家的月收入为11650元,则小明家3月份最多能用水多少吨?
【应用迁移】
一个不等式常常可以有不同的实际意义。
例如,不等式3x+4≤21的实际意义可以是:
小明准备用21元钱买笔和笔记本。已知笔每支3元,笔记本每本4元,如果小明买了1本笔记本,那么他最多还可以买几支笔?
你能给出这个不等式不同的实际意义吗?
小结反思
用一元一次不等式的知识解决实际问题务必注意:
1、静心读题,弄清题意,找出题中不等关系;标出关键的词语和句子,让题意清晰简单化;对于有图表的问题,要认真分析图表中的每个量,单位都不能放过。
2、设未知数后,根据关键的句子,用含未知数的代数式表示相关的量,再根据不等关系建立不等式。
谢谢聆听!
用一元一次不等式解决问题复习
【要点梳理】
要点一、用 数学知识 解决 实际问题 的通用思路
实际问题
数学问题
数学问题的解
检验,回答
(包含不等关系)
(列一元一次不等式)
(x>a,x
解数学问题
解一元一次不等式
【要点梳理】
要点二、列不等式解决实际问题的步骤
列一元一次不等式解决实际问题与列一元一次方程、二元一次方程组解决实际问题类似,通常也需要经过以下几个步骤:
(1)审:认真审题,分清已知量、未知量及其关系,找出题中不等关系要抓住题中的关键字眼,如“大于”、“小于”、“不大于”、“至少”、“超过”、“不超过”等;
(2)设:设出适当的未知数。在设未知数时,表示不等关系的文字如“至少”“最多”等不能出现,即应给出肯定的未知数的设法;
(3)列:根据题中的不等关系,列出不等式;
(4)解:解所列的不等式;
(5)验:检验求得的解集是否正确、是否符合实际意义;
(6)答:写出答案,把表示不等关系的文字补上。
【基础练习】
1.某汽车厂改进生产工艺后,每天生产的汽车比原来每天生产的汽车多6辆,那么现在15天的产量就超过了原来20天的产量,设原来每天生产汽车x辆,则列出的不等式为( )
A.15x>20(x+6) B.15(x+6)>20x C.15x>20(x-6) D.15(x-6)>20x
【解析】 由题意得:15(x+6)>20x
B
2.喜迎建党100周年,某校举行党史知识竞赛,共30道题,每道题都给出4个答案,其中只有一个答案正确,选对得4分,不选或选错扣2分,得分不低于80分得奖,那么得奖至少应选对的题数是( )
A.23 B.24 C.25 D.26
B
【解析】设选对x道题,则不选或选错(30﹣x)道题,
依题意,得:4x﹣2(30﹣x)≥80,
解得: .
∵x为正整数,
∴要得奖至少应选对24道题
【基础练习】
3.某种商品的进价为500元,出售时标价为750元,由于换季,商店准备打折销售,但要保持利润不低于20%,那么至多打( )
A.6折 B.7折 C.8折 D.9折
C
【解析】设该商品打x折销售,
依题意得: ,
解得:x≥8.
【基础练习】
4.“垃圾分类做得好,明天生活会更好”,学校需要购买分类垃圾桶10个,放在校园的公共区域,市场上有A型和B型两种分类垃圾桶,A型分类垃圾桶350元/个,B型分类垃圾桶400元/个,总费用不超过3650元,则不同的购买方式有( )
A.2种 B.3种 C.4种 D.5种
【解析】设购买A型分类垃圾桶x个,则购买B型分类垃圾桶(10﹣x)个
依题意,得:350x+400(10﹣x)≤3650,
解得:x≥7.
∵x,(10﹣x)均为非负整数,
∴x可以为7,8,9,10,
∴共有4种购买方案.
C
【基础练习】
计算提醒:先同除以50,再去括号计算
7x+8(10-x)≤73
5.某种型号汽车每行驶100km耗油10L,其油箱容量为40L.为了有效延长汽车使用寿命,厂家建议每次加油时油箱内剩余油量不低于油箱容量的 ,按此建议,一辆加满油的该型号汽车最多行驶的路程是 _____ km.
350
【解析】设行驶xkm,
∵油箱内剩余油量不低于油箱容量的,
∴ .
∴x≤350
故该辆汽车最多行驶的路程是350km。
【基础练习】
6.小明受《乌鸦喝水》故事的启发,利用量筒和体积相同的小球进行了如下操作,请根据图中给出的信息,量筒中至少放入 个小球时有水溢出.
11
不等关系:原来水的高度+放入x个小球后水上升的高度>量筒的高度
【解析】由题意可得每添加一个球,水面上升 cm
设放入x个小球时有水溢出,则
解得
即至少放入11个小球时有水溢出.
【基础练习】
【典型例题】类型一、营销问题
例1.(2020春 常州期末)2020年初,由于新冠病毒的蔓延,口罩市场出现热销,小明的爸爸用18000元购进甲、乙两种型号的口罩,在自家药店销售,销售完后共获利3900元,进价和售价如表所示:
价格型号 甲种型号口罩 乙种型号口罩
进价(元/袋) 20 30
售价(元/袋) 25 36
(1)小明爸爸的药店购进甲、乙两种型号的口罩各多少袋?
解:(1)设小明爸爸的商店购进甲种型号口罩x袋,乙种型号口罩y袋,
根据题意得,
解得:
答:小明爸爸的药店购进甲种型号口罩300袋,乙种型号口罩400袋;
例1.(2020春 常州期末)2020年初,由于新冠病毒的蔓延,口罩市场出现热销,小明的爸爸用18000元购进甲、乙两种型号的口罩,在自家药店销售,销售完后共获利3900元,进价和售价如表所示:
价格型号 甲种型号口罩 乙种型号口罩
进价(元/袋) 20 30
售价(元/袋) 25 36
(2)设需购进a袋乙种型号的口罩,则需购进甲种型号的口罩(800-a)袋
根据题意得,(25﹣20)(800﹣a)+(36﹣30)a≥4500.
解这个不等式,得a≥500.
答:至少需购进500袋乙种型号的口罩.
(2)由于需求量大,口罩很快售完,小明的爸爸决定再一次购进甲、乙两种型号的口罩共800袋.如果要使这800袋口罩全部售完后所得利润不低于4500元,那么至少需购进多少袋乙种型号的口罩?
【典型例题】类型一、营销问题
例2.计划对河道进行改造,现有甲乙两个工程队参加改造施工,受条件限制,每天只能由一个工程队施工.若甲工程队先单独施工3天,再由乙工程队单独施工5天,则可以完成550米施工任务;若甲工程队先单独施工2天,再由乙工程对单独施工4天,则可以完成420米的施工任务.
(1)求甲、乙两个工程队平均每天分别能完成多少米施工任务?
(2)该河道全长6000米,若两队合作工期不能超过90天,乙工程队至少施工多少天?
解:(1)设甲工程队平均每天施工x米,
乙工程队平均每天施工y米,
根据题意得:
解得:
答:甲工程队平均每天能完成施工任务50米,
乙工程队平均每天能完成施工任务80米.
(2)设乙工程队施工a天,
则甲工程队施工(90-a)天
根据题意得:50(90-a)+80a≥6000,
解得:a≥50,
答:乙工程队至少施工50天.
【典型例题】类型二、工程问题
如果工作90天,完成的河道应不少于6000米
例3.联通公司推出两种手机收费方案.方案一:月租费36元,本地通话话费0.1元/分;方案二:不收月租费,本地通话费为0.6元/分.设小明的爸爸一个月通话时间为x分钟.小明爸爸选择哪种方案才合算呢?
解:
由题意得,方案一需付费(36+0.1x)元,
方案二需付费0.6x元。
∴当36+0.1x<0.6x,即x>72时,方案一比方案二优惠,此时小明爸爸选择方案一合算;
当36+0.1x=0.6x,即x=72时,两种方案费用相同,小明爸爸均可选择;
当36+0.1x>0.6x,即x<72时,方案二比方案一优惠,此时小明爸爸选择方案二合算。
【典型例题】类型三、方案选择
例4.为了让市民树立起“珍惜水、节约水、保护水”的用水理念,居民生活用水按阶梯式计算水价,水价计算方式如表所示,每吨水还需另加污水处理费0.60元.已知小明家今年1月份用水20吨,交水费60元;2月份用水25吨,交水费79元.(友情提示:水费=水价+污水处理费)
(1)求m,n的值.
解:(1)由题意得
解得
答:m的值为2.4,n的值为3.2。
(2)2%×11650=233(元),
由(1)得m=2.4,n=3.2,
当用水量为30吨时,水费为:20×2.4+10×3.2+30×0.6=98(元),
∵233>98,∴小明家3月份用水量超过30吨.
可设小明家3月份用水x吨,
由题意得20×2.4+10×3.2+2×2.4(x﹣30)+0.6x≤233
或98+(2×2.4+0.6)(x﹣30)≤233,
解得x≤55,答:小明家3月份最多能用水55吨.
【典型例题】类型四、分段收费
用水量 水价(元/吨)
不超过20吨 m
超过20吨且不超过30吨的部分 n
超过30吨的部分 2m
(2)为了节省开支,小明计划把3月份的水费控制在不超过家庭月收入的2%.若小明家的月收入为11650元,则小明家3月份最多能用水多少吨?
【应用迁移】
一个不等式常常可以有不同的实际意义。
例如,不等式3x+4≤21的实际意义可以是:
小明准备用21元钱买笔和笔记本。已知笔每支3元,笔记本每本4元,如果小明买了1本笔记本,那么他最多还可以买几支笔?
你能给出这个不等式不同的实际意义吗?
小结反思
用一元一次不等式的知识解决实际问题务必注意:
1、静心读题,弄清题意,找出题中不等关系;标出关键的词语和句子,让题意清晰简单化;对于有图表的问题,要认真分析图表中的每个量,单位都不能放过。
2、设未知数后,根据关键的句子,用含未知数的代数式表示相关的量,再根据不等关系建立不等式。
谢谢聆听!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
