华师大版数学七年级上册同步课件:2.3相反数(共16张PPT)
文档属性
| 名称 | 华师大版数学七年级上册同步课件:2.3相反数(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 257.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-25 18:35:21 | ||
图片预览





文档简介
(共16张PPT)
第二章 有理数
2.3 相反数
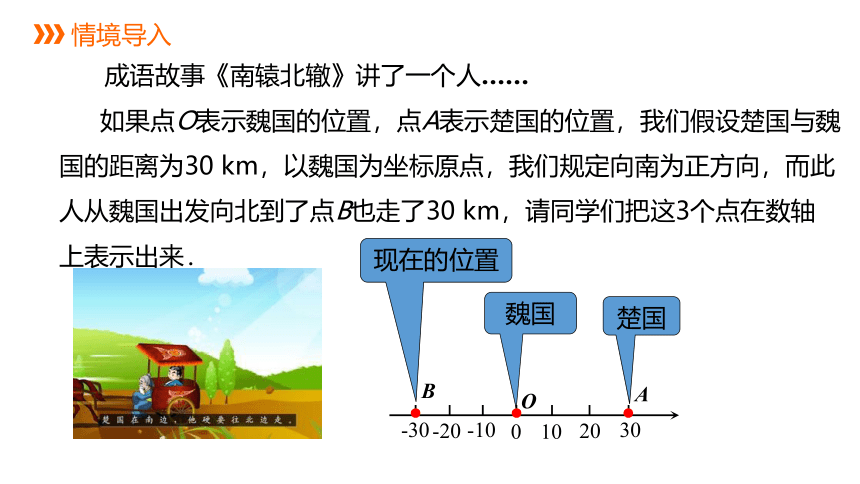
成语故事《南辕北辙》讲了一个人……
如果点O表示魏国的位置,点A表示楚国的位置,我们假设楚国与魏国的距离为30 km,以魏国为坐标原点,我们规定向南为正方向,而此人从魏国出发向北到了点B也走了30 km,请同学们把这3个点在数轴上表示出来.
现在的位置
魏国
楚国
O
A
-30
-20
-10
0
10
20
30
●
●
●
B
情境导入
O
A
●
●
●
B
-30
-10
0
10
20
30
-20
40
50
-40
-50
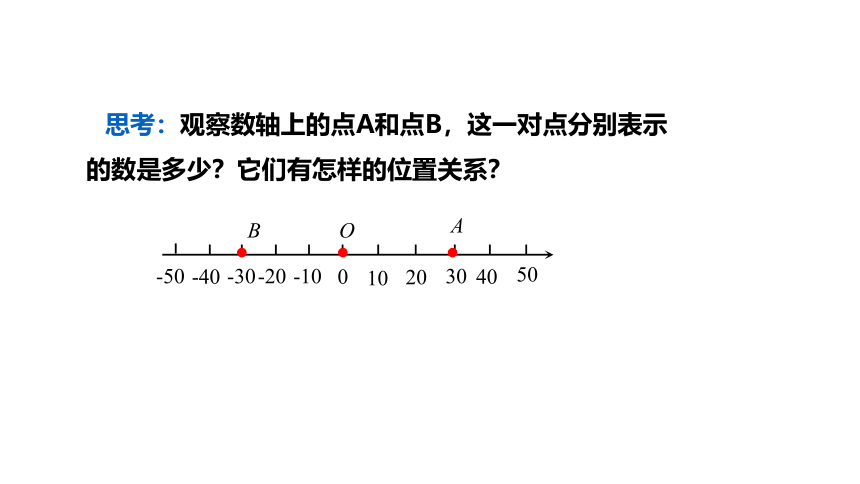
思考:观察数轴上的点A和点B,这一对点分别表示的数是多少?它们有怎样的位置关系?
知识回顾
这两对数有什么共同点?
每对中的两个数,都只有正负号不同.
做一做:
在数轴上,画出表示以下两对数的点:
-6和6,1.5和-1.5.
像30和-30, 6和-6,1.5和-1.5这样,只有正负号不同的两个数称
互为相反数.也就是说,其中一个数是另一个数的相反数.
例如,6和-6互为相反数,
6是-6的相反数,
-6是6的相反数.
相反数是成对出现的.
只有正负号不同
包含两层意义:
(1)符号相反;
(2)所含的数字相同.
1.代数意义:只有正负号不同的两个数称互为相反数.
特殊规定:0的相反数是0.
几何意义:在数轴上表示互为相反数的两个点分别位于原点的两旁,且与原点的距离相等.
获取新知
要点精析:
(1)相反数是两个数之间的特殊关系,是成对出现的,不能单独存在.
(2)任何一个有理数,都只有一个相反数.
(3)“只有”指的是除符号不同外,其他完全相同.
(4)相反数与前面所学的“相反意义的量”是不同的概念.
例题讲解
例1 分别写出下列各数的相反数:
+5,-7, ,11.2.
解:+5的相反数是-5,-7的相反数是7,
的相反数是
11.2的相反数是-11.2.
总结:正数的相反数是负数,负数的相反数是正数.
1. 相反数的求法:
(1)求一个数的相反数就是在这个数的前面加上“-”号,
即a的相反数是-a,(这里a可以是正数、负数、0)
(2)求一个式子的相反数,一定要将整个式子加上括号,再在括号前面添上“-”号.例如:a-b的相反数是-(a-b)
当a是正数时,-a是_____
负数
当a是负数时,-a是_____
正数
当a是0时,-a是___
0
注意:-a不一定是负数哦!
0是唯一一个相反数等于它本身的数.
2. 相反数的性质:
若a、b互为相反数,则a+b=0(a=-b,b=-a);反过来,
若a+b=0,则a、b互为相反数.
即:
a、b互为相反数
a+b=0.
获取新知
多重符号的化简
我们通常在一个数的前面添上“﹣”号,表示这个数的相反数.
例如:﹣4的相反数为:﹣(﹣4)=4
+5.5的相反数为:﹣(+5.5)=﹣5.5.
在一个数的前面添上“+”号,仍表示这个数本身.
例如:+(﹣4)=﹣4, +(+12)=12.
例题讲解
例2 化简:(先读后写)
(1)-( +10); (2) +( -0.15); (3) +( +3); ⑷-(-20).
(5)-[+(-7)] (6)-[-(-1.1)]
解:(1)-( +10)=-10.
(2)+ (- 0. 15)= - 0. 15.
(3)+( + 3) = + 3 = 3.
(4)- ( -20) =20.
(5)-[+(-7)] =7
(6) -[-(-1.1)]=-1.1
由内向外依次去括号
多重符号的化简技巧:
含有多种符号时,“+”的个数不影响化简的结果,
若一个数的前面有偶数个“-”号,则化简后的结果为正;
若一个数的前面有奇数个“-”号,则化简后的结果为负.
简记为“奇负、偶正”
随堂演练
1.在数轴上,数2和-2所对应的点位于原点的 ,且与原点的距
离都等于 ,则2的相反数为 ,-2的相反数为 .
2.下列四组数中,相等的一组是 ( )
A.+2与+(-2) B.-(+8)与+8
C.-(-2)与-2 D.+(-1)与-(+1)
两旁
2
-2
2
D
3.数轴上表示互为相反数的两点的距离为10个单位长度,则这两个数分别为( )
A. 0 和 10 B. -10 和 0
C. 10 和 -10 D. -5 和 5
D
课堂小结
知识点一 相反数的概念
正负号不同
零
知识点二 相反数的几何意义
两旁
相等
知识点三 带多重符号的化简
相反数
相等
第二章 有理数
2.3 相反数
成语故事《南辕北辙》讲了一个人……
如果点O表示魏国的位置,点A表示楚国的位置,我们假设楚国与魏国的距离为30 km,以魏国为坐标原点,我们规定向南为正方向,而此人从魏国出发向北到了点B也走了30 km,请同学们把这3个点在数轴上表示出来.
现在的位置
魏国
楚国
O
A
-30
-20
-10
0
10
20
30
●
●
●
B
情境导入
O
A
●
●
●
B
-30
-10
0
10
20
30
-20
40
50
-40
-50
思考:观察数轴上的点A和点B,这一对点分别表示的数是多少?它们有怎样的位置关系?
知识回顾
这两对数有什么共同点?
每对中的两个数,都只有正负号不同.
做一做:
在数轴上,画出表示以下两对数的点:
-6和6,1.5和-1.5.
像30和-30, 6和-6,1.5和-1.5这样,只有正负号不同的两个数称
互为相反数.也就是说,其中一个数是另一个数的相反数.
例如,6和-6互为相反数,
6是-6的相反数,
-6是6的相反数.
相反数是成对出现的.
只有正负号不同
包含两层意义:
(1)符号相反;
(2)所含的数字相同.
1.代数意义:只有正负号不同的两个数称互为相反数.
特殊规定:0的相反数是0.
几何意义:在数轴上表示互为相反数的两个点分别位于原点的两旁,且与原点的距离相等.
获取新知
要点精析:
(1)相反数是两个数之间的特殊关系,是成对出现的,不能单独存在.
(2)任何一个有理数,都只有一个相反数.
(3)“只有”指的是除符号不同外,其他完全相同.
(4)相反数与前面所学的“相反意义的量”是不同的概念.
例题讲解
例1 分别写出下列各数的相反数:
+5,-7, ,11.2.
解:+5的相反数是-5,-7的相反数是7,
的相反数是
11.2的相反数是-11.2.
总结:正数的相反数是负数,负数的相反数是正数.
1. 相反数的求法:
(1)求一个数的相反数就是在这个数的前面加上“-”号,
即a的相反数是-a,(这里a可以是正数、负数、0)
(2)求一个式子的相反数,一定要将整个式子加上括号,再在括号前面添上“-”号.例如:a-b的相反数是-(a-b)
当a是正数时,-a是_____
负数
当a是负数时,-a是_____
正数
当a是0时,-a是___
0
注意:-a不一定是负数哦!
0是唯一一个相反数等于它本身的数.
2. 相反数的性质:
若a、b互为相反数,则a+b=0(a=-b,b=-a);反过来,
若a+b=0,则a、b互为相反数.
即:
a、b互为相反数
a+b=0.
获取新知
多重符号的化简
我们通常在一个数的前面添上“﹣”号,表示这个数的相反数.
例如:﹣4的相反数为:﹣(﹣4)=4
+5.5的相反数为:﹣(+5.5)=﹣5.5.
在一个数的前面添上“+”号,仍表示这个数本身.
例如:+(﹣4)=﹣4, +(+12)=12.
例题讲解
例2 化简:(先读后写)
(1)-( +10); (2) +( -0.15); (3) +( +3); ⑷-(-20).
(5)-[+(-7)] (6)-[-(-1.1)]
解:(1)-( +10)=-10.
(2)+ (- 0. 15)= - 0. 15.
(3)+( + 3) = + 3 = 3.
(4)- ( -20) =20.
(5)-[+(-7)] =7
(6) -[-(-1.1)]=-1.1
由内向外依次去括号
多重符号的化简技巧:
含有多种符号时,“+”的个数不影响化简的结果,
若一个数的前面有偶数个“-”号,则化简后的结果为正;
若一个数的前面有奇数个“-”号,则化简后的结果为负.
简记为“奇负、偶正”
随堂演练
1.在数轴上,数2和-2所对应的点位于原点的 ,且与原点的距
离都等于 ,则2的相反数为 ,-2的相反数为 .
2.下列四组数中,相等的一组是 ( )
A.+2与+(-2) B.-(+8)与+8
C.-(-2)与-2 D.+(-1)与-(+1)
两旁
2
-2
2
D
3.数轴上表示互为相反数的两点的距离为10个单位长度,则这两个数分别为( )
A. 0 和 10 B. -10 和 0
C. 10 和 -10 D. -5 和 5
D
课堂小结
知识点一 相反数的概念
正负号不同
零
知识点二 相反数的几何意义
两旁
相等
知识点三 带多重符号的化简
相反数
相等
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
