华师大版数学七年级上册同步课件:2.9.2第1课时有理数的乘法交换律和结合律(共20张PPT)
文档属性
| 名称 | 华师大版数学七年级上册同步课件:2.9.2第1课时有理数的乘法交换律和结合律(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 325.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-25 19:03:32 | ||
图片预览







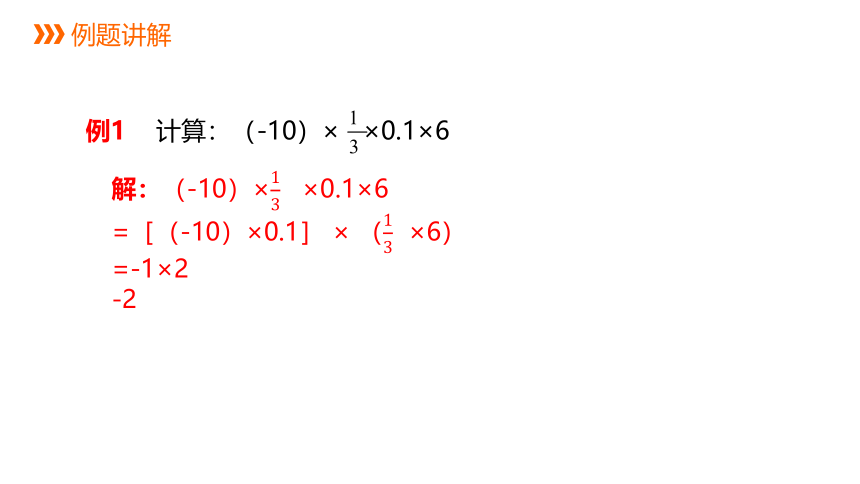

文档简介
(共20张PPT)
第二章 有理数
2.9.2 第1课时 有理数的乘法交换律和结合律
知识回顾
1.有理数的乘法法则是什么?
3.小学学过乘法的哪些运算律?
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数和零相乘,都得0
乘法交换律、乘法结合律、乘法分配律
2.有理数相乘的步骤:
先确定积的符号,再把绝对值相乘,当有一个因数为零时,积为零.
获取新知
3×5=5×3
(3×5)×2=3×(5×2)
3×(5+2)=3×5+3×2
思考:引入负数后,三种运算律是否还成立呢?
在小学里,我们都知道,数的乘法满足交换律、结合律和分配律,例如
(1)任意选择两个有理数(至少有一个是负数),
分别填人下列□和〇内,并比较两个运算结果:
□ ×〇和〇 × □ ;
获取新知
探究
例如:5×(-6)=-30
(-6)×5 =-30
5×(-6)=(-6)×5
比较它们的结果,你发现了什么?
有理数的乘法仍满足交换律
乘法交换律:两个数相乘,交换因数的位置,积不变.
ab = ba.
(2)任意选择三个有理数(至少有一个是负数),
分别填入下列□、〇和◇内,并比较两个运算
结果:(□×〇)× ◇ 和□×(〇 × ◇).
你能发现什么?
获取新知
探究
[3×(-4)]×(-5)=(-12)×(-5)=60
3×[(-4)×(-5)]=3×20=60
比较它们的结果,你发现了什么?
[3×(-4)]×(-5)=3×[(-4)×(-5)]
有理数的乘法仍满足结合律.
乘法结合律:三个数相乘,先把前两个数相乘,或者先把
后两个数相乘,积不变.
(ab)c = a(bc) .
根据乘法交换律和结合律,三个或三个以上的有理
数相乘,可以任意交换因数的位置,也可以先把其中的几
个数相乘.
例题讲解
例1 计算:(-10)× ×0.1×6
解:(-10)× ×0.1×6
=[(-10)×0.1] × ( ×6)
=-1×2
-2
从例1的解答过程中,你能得到什么启发?试直接
写出下列各式的结果:
(- 10) ×(- ) × 0.1 × 6 = ;
(-10) × (- ) ×(-0.1) × 6= ;
(-10) × (- ) ×( - 0.1) ×( - 6) = .
2
-2
2
几个不等于0的数相乘,你发现结果的符号与哪些因素有关 如果其中一个因数是0,结果又是多少?
思考
几个不等于零的数相乘,积的符号由______________决定.
当负因数有_____个时,积为负;
当负因数有_____个时,积为正.
要点归纳:
负因数的个数
奇数
偶数
}
奇负偶正
几个不等于零的数相乘,首先确定积的正负号,然后把绝对值相乘.
试一试
(-5)×(-8.1)×3.14×0=__________.
几个数相乘,有一个因数为零,积就为零.
(-5)×(- )×3×(-2)×2=_____________
-30
0
例题讲解
例2 计算:
(1)8+(- )×(-8)×
(2)(-3)× ×(- )×(- )
(3)(- )×5×0×
解:(1)8+(- )×(-8)×
=8+3
=11
运算顺序:先计算三个有理数相乘,再算加法.三个不等于零的有理数相乘,先根据“负因数的个数确定积的正负号,再把绝对值相乘.
(2)(-3)× ×(- )×(- )
四个不等于零的数相乘,先确定积的正负号,再把绝对值相乘.
奇负偶正
= - 3× × ×
=-
(3)(- )×5×0× =0
根据”几个数相乘,有一个因数为零,积就为零.
思考
三个数相乘,如果积为负,其中可能有几个因
数为负数?四个数相乘,如果积为正,其中可能有
几个因数为负数?
三个数相乘,若积为负,负数的个数是奇数个,因而可能是1个或3个因数为负数.
四个数相乘,若积为正,则负数的个数是偶数个,因而可能是0个或2个或4个因素是负数.
1. 若五个有理数相乘的积为正数,则五个数中负数的个数是( )
A.0 B.2 C.4 D.0或2或4
2. 有2 016个有理数相乘,如果积为0,那么在2 016个有理数中( )
A.全部为0 B.只有一个因数为0
C.至少有一个为0 D.有两个数互为相反数
D
C
随堂演练
3.计算:
解:
课堂小结
知识点一 有理数乘法的运算律
知识点二 多个数相乘
第二章 有理数
2.9.2 第1课时 有理数的乘法交换律和结合律
知识回顾
1.有理数的乘法法则是什么?
3.小学学过乘法的哪些运算律?
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数和零相乘,都得0
乘法交换律、乘法结合律、乘法分配律
2.有理数相乘的步骤:
先确定积的符号,再把绝对值相乘,当有一个因数为零时,积为零.
获取新知
3×5=5×3
(3×5)×2=3×(5×2)
3×(5+2)=3×5+3×2
思考:引入负数后,三种运算律是否还成立呢?
在小学里,我们都知道,数的乘法满足交换律、结合律和分配律,例如
(1)任意选择两个有理数(至少有一个是负数),
分别填人下列□和〇内,并比较两个运算结果:
□ ×〇和〇 × □ ;
获取新知
探究
例如:5×(-6)=-30
(-6)×5 =-30
5×(-6)=(-6)×5
比较它们的结果,你发现了什么?
有理数的乘法仍满足交换律
乘法交换律:两个数相乘,交换因数的位置,积不变.
ab = ba.
(2)任意选择三个有理数(至少有一个是负数),
分别填入下列□、〇和◇内,并比较两个运算
结果:(□×〇)× ◇ 和□×(〇 × ◇).
你能发现什么?
获取新知
探究
[3×(-4)]×(-5)=(-12)×(-5)=60
3×[(-4)×(-5)]=3×20=60
比较它们的结果,你发现了什么?
[3×(-4)]×(-5)=3×[(-4)×(-5)]
有理数的乘法仍满足结合律.
乘法结合律:三个数相乘,先把前两个数相乘,或者先把
后两个数相乘,积不变.
(ab)c = a(bc) .
根据乘法交换律和结合律,三个或三个以上的有理
数相乘,可以任意交换因数的位置,也可以先把其中的几
个数相乘.
例题讲解
例1 计算:(-10)× ×0.1×6
解:(-10)× ×0.1×6
=[(-10)×0.1] × ( ×6)
=-1×2
-2
从例1的解答过程中,你能得到什么启发?试直接
写出下列各式的结果:
(- 10) ×(- ) × 0.1 × 6 = ;
(-10) × (- ) ×(-0.1) × 6= ;
(-10) × (- ) ×( - 0.1) ×( - 6) = .
2
-2
2
几个不等于0的数相乘,你发现结果的符号与哪些因素有关 如果其中一个因数是0,结果又是多少?
思考
几个不等于零的数相乘,积的符号由______________决定.
当负因数有_____个时,积为负;
当负因数有_____个时,积为正.
要点归纳:
负因数的个数
奇数
偶数
}
奇负偶正
几个不等于零的数相乘,首先确定积的正负号,然后把绝对值相乘.
试一试
(-5)×(-8.1)×3.14×0=__________.
几个数相乘,有一个因数为零,积就为零.
(-5)×(- )×3×(-2)×2=_____________
-30
0
例题讲解
例2 计算:
(1)8+(- )×(-8)×
(2)(-3)× ×(- )×(- )
(3)(- )×5×0×
解:(1)8+(- )×(-8)×
=8+3
=11
运算顺序:先计算三个有理数相乘,再算加法.三个不等于零的有理数相乘,先根据“负因数的个数确定积的正负号,再把绝对值相乘.
(2)(-3)× ×(- )×(- )
四个不等于零的数相乘,先确定积的正负号,再把绝对值相乘.
奇负偶正
= - 3× × ×
=-
(3)(- )×5×0× =0
根据”几个数相乘,有一个因数为零,积就为零.
思考
三个数相乘,如果积为负,其中可能有几个因
数为负数?四个数相乘,如果积为正,其中可能有
几个因数为负数?
三个数相乘,若积为负,负数的个数是奇数个,因而可能是1个或3个因数为负数.
四个数相乘,若积为正,则负数的个数是偶数个,因而可能是0个或2个或4个因素是负数.
1. 若五个有理数相乘的积为正数,则五个数中负数的个数是( )
A.0 B.2 C.4 D.0或2或4
2. 有2 016个有理数相乘,如果积为0,那么在2 016个有理数中( )
A.全部为0 B.只有一个因数为0
C.至少有一个为0 D.有两个数互为相反数
D
C
随堂演练
3.计算:
解:
课堂小结
知识点一 有理数乘法的运算律
知识点二 多个数相乘
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
