华师大版数学七年级上册同步课件:3.1.1用字母表示数(共17张PPT)
文档属性
| 名称 | 华师大版数学七年级上册同步课件:3.1.1用字母表示数(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 673.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-25 19:20:13 | ||
图片预览






文档简介
(共17张PPT)
第三章 整式的加减
3.1列代数式
第1课时 用字母表示数
情景导入
鸡1只,兔1只,有头____个,脚____只;
鸡3只,兔4只,有头____个,脚____只;
鸡2只,兔2只,有头____个,脚____只;
鸡a只,兔b只,有头多少个 脚多少只?
2
6
4
12
7
22
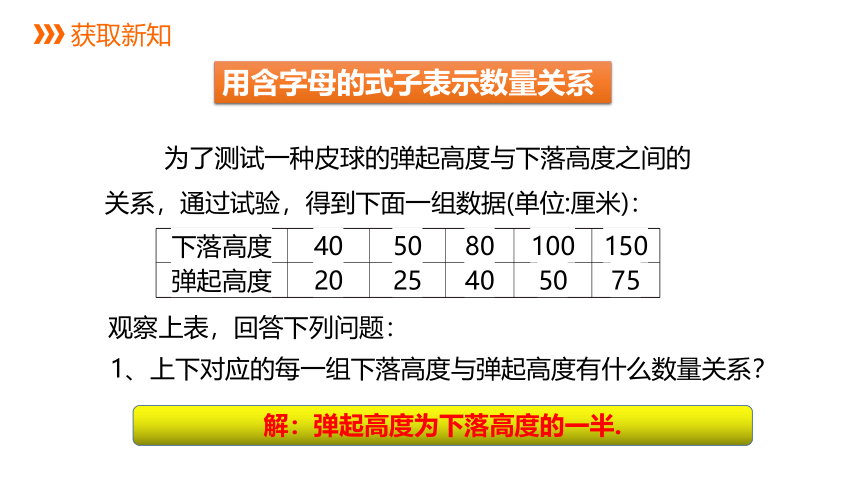
获取新知
用含字母的式子表示数量关系
为了测试一种皮球的弹起高度与下落高度之间的
关系,通过试验,得到下面一组数据(单位:厘米):
下落高度 40 50 80 100 150
弹起高度 20 25 40 50 75
观察上表,回答下列问题:
1、上下对应的每一组下落高度与弹起高度有什么数量关系?
解:弹起高度为下落高度的一半.
2、如果我们用字母b表示下落高度的厘米数,那么对应的弹起高度为________(厘米).
让我们再看几个用字母表示数的例子:
(1)如果用a、b表示任意两个有理数,那么加法交
换律可以表示为:a + b = b + a.
乘法交换律可以表示为:ab = ba.
你能用字母表示有理数的其它几个运算律吗?试一试.
(2)某种大米每千克的售价是4. 8元,购买这种大米2
千克、2.5千克、5千克、10千克各需付款多少元?
购买这种大米2千克需付款4. 8×2=9. 6(元);
购买这种大米2. 5千克需付款4. 8×2. 5=12(元);
购买这种大米5千克需付款______________(元);
购买这种大米10千克需付款______________(元);
4. 8×5=24
4. 8×10=48
如果用字母n表示购买这种大米的千克数,那么
需 付款_______元.
用这个式子,可由
购买大米的千克数(n),
箅出所需的付款数.
4.8n
(3)我们知道,长方形的面积等于长与宽的积.如果
用a、b分别表示长方形的长和宽,用S表示长方形
的面积,则有长方形的面积公式:S=ab.
意义:用字母表示数之后,有些数量之间的关系用含有字母的式子表示,看上去更加简明,更具有普遍意义了.
例1 填空:
(1)某地为了治理河山,改造环境,计划在第十
二个五年计划期间植树绿化荒山,如果每年
植树绿化n公顷,那么这五年内可以植树绿化
荒山______公顷;
5n
例题讲解
(2)每本练习本m元,甲买了5本,乙买了2本,两人一花了___________元,甲比乙多花了___________元;
(3)1 500米跑步测试,如果某同学跑完全程的成绩是t秒,
那么他跑步的平均速度是_______米/秒.
(5m+2m)
(5m-2m)
(1)数字与字母相乘或字母与字母相乘,乘号通常写作“ ”或省略不写,如这里5×n常写作5 n或5n; 但数与数相乘,仍使用“×”号.
(2)数字与字母相乘时,数字通常写在字母前面,如5n
一 般不写成n5;
(3)除法运算写成分数形式,如1 500÷t 通常写作
(t≠0).
!
用字母表示数的书写要求:
(4)带分数与字母相乘时,带分数要写成假分数.如 xy应写成 xy
(5)式子是和(或差)的形式,且后面有单位时,式子要用括号括起来(如例题2题).
随堂演练
1 填空:
(1) 一打铅笔有12支,n打铅笔有_______支;
(2)三角形的三边长分别为3a、4a、5a,其周长为
______;
(3)如图,某广场四角铺上了四分之
一圆形的草地,若圆形的半径为
r 米,则共有草地_____平方米.
12n
12a
πr2
2.“比a的 倍大1的数”用式子表示为( )
A. B.
C. D.
A
问题:鸡a只,兔b只,有头多少个 脚多少只?
你会了吗 ?
解:有头(a+b)个,脚有(2a+4b)只.
课堂小结
知识点 用字母表示数
用字母表示数的书写要求:
(1)数字与字母相乘或字母与字母相乘,乘号通常写作“ ”
或省略不写,但数与数相乘,仍使用“×”号.
(2)数字与字母相乘时,数字通常写在字母前面.
(3)除法运算写成分数形式.
(4)带分数与字母相乘时,带分数要写成假分数.
(5)式子是和(或差)的形式,且后面有单位时,式子
要用括号括起来.
第三章 整式的加减
3.1列代数式
第1课时 用字母表示数
情景导入
鸡1只,兔1只,有头____个,脚____只;
鸡3只,兔4只,有头____个,脚____只;
鸡2只,兔2只,有头____个,脚____只;
鸡a只,兔b只,有头多少个 脚多少只?
2
6
4
12
7
22
获取新知
用含字母的式子表示数量关系
为了测试一种皮球的弹起高度与下落高度之间的
关系,通过试验,得到下面一组数据(单位:厘米):
下落高度 40 50 80 100 150
弹起高度 20 25 40 50 75
观察上表,回答下列问题:
1、上下对应的每一组下落高度与弹起高度有什么数量关系?
解:弹起高度为下落高度的一半.
2、如果我们用字母b表示下落高度的厘米数,那么对应的弹起高度为________(厘米).
让我们再看几个用字母表示数的例子:
(1)如果用a、b表示任意两个有理数,那么加法交
换律可以表示为:a + b = b + a.
乘法交换律可以表示为:ab = ba.
你能用字母表示有理数的其它几个运算律吗?试一试.
(2)某种大米每千克的售价是4. 8元,购买这种大米2
千克、2.5千克、5千克、10千克各需付款多少元?
购买这种大米2千克需付款4. 8×2=9. 6(元);
购买这种大米2. 5千克需付款4. 8×2. 5=12(元);
购买这种大米5千克需付款______________(元);
购买这种大米10千克需付款______________(元);
4. 8×5=24
4. 8×10=48
如果用字母n表示购买这种大米的千克数,那么
需 付款_______元.
用这个式子,可由
购买大米的千克数(n),
箅出所需的付款数.
4.8n
(3)我们知道,长方形的面积等于长与宽的积.如果
用a、b分别表示长方形的长和宽,用S表示长方形
的面积,则有长方形的面积公式:S=ab.
意义:用字母表示数之后,有些数量之间的关系用含有字母的式子表示,看上去更加简明,更具有普遍意义了.
例1 填空:
(1)某地为了治理河山,改造环境,计划在第十
二个五年计划期间植树绿化荒山,如果每年
植树绿化n公顷,那么这五年内可以植树绿化
荒山______公顷;
5n
例题讲解
(2)每本练习本m元,甲买了5本,乙买了2本,两人一花了___________元,甲比乙多花了___________元;
(3)1 500米跑步测试,如果某同学跑完全程的成绩是t秒,
那么他跑步的平均速度是_______米/秒.
(5m+2m)
(5m-2m)
(1)数字与字母相乘或字母与字母相乘,乘号通常写作“ ”或省略不写,如这里5×n常写作5 n或5n; 但数与数相乘,仍使用“×”号.
(2)数字与字母相乘时,数字通常写在字母前面,如5n
一 般不写成n5;
(3)除法运算写成分数形式,如1 500÷t 通常写作
(t≠0).
!
用字母表示数的书写要求:
(4)带分数与字母相乘时,带分数要写成假分数.如 xy应写成 xy
(5)式子是和(或差)的形式,且后面有单位时,式子要用括号括起来(如例题2题).
随堂演练
1 填空:
(1) 一打铅笔有12支,n打铅笔有_______支;
(2)三角形的三边长分别为3a、4a、5a,其周长为
______;
(3)如图,某广场四角铺上了四分之
一圆形的草地,若圆形的半径为
r 米,则共有草地_____平方米.
12n
12a
πr2
2.“比a的 倍大1的数”用式子表示为( )
A. B.
C. D.
A
问题:鸡a只,兔b只,有头多少个 脚多少只?
你会了吗 ?
解:有头(a+b)个,脚有(2a+4b)只.
课堂小结
知识点 用字母表示数
用字母表示数的书写要求:
(1)数字与字母相乘或字母与字母相乘,乘号通常写作“ ”
或省略不写,但数与数相乘,仍使用“×”号.
(2)数字与字母相乘时,数字通常写在字母前面.
(3)除法运算写成分数形式.
(4)带分数与字母相乘时,带分数要写成假分数.
(5)式子是和(或差)的形式,且后面有单位时,式子
要用括号括起来.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
