华师大版数学七年级上册同步课件:3.3.2多项式(共12张PPT)
文档属性
| 名称 | 华师大版数学七年级上册同步课件:3.3.2多项式(共12张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 314.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-25 19:31:51 | ||
图片预览





文档简介
(共12张PPT)
第三章 整式的加减
3.3 整式 第2课时 多项式
知识回顾
列代数式:
(1)若三角形的三条边长分别为a、b、c,则三角形
的周长是__________ ;
(2)某班有男生x人,女生21人,这个班的学生一共
有_________人;
a+b+c
(x+21)
(3)图中阴影部分的面积为___________.
列出的这些代数式有什
么共同特点 它们与单
项式有什么区别?
2ar-πr2
获取新知
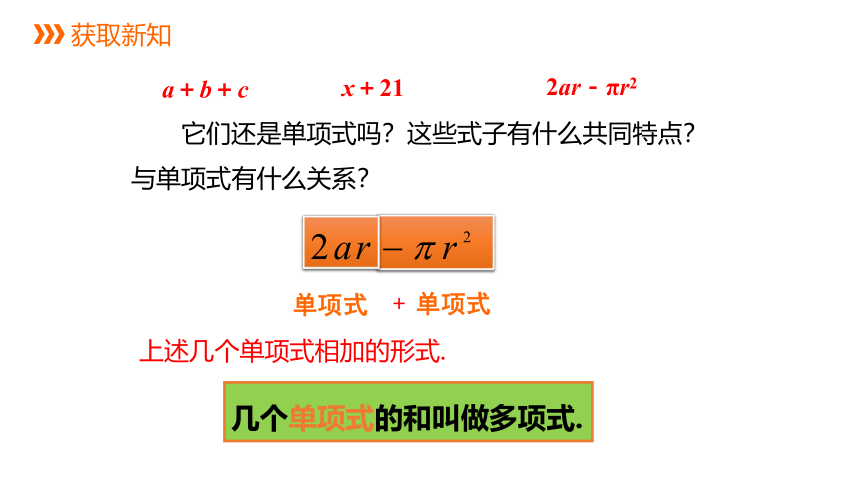
几个单项式的和叫做多项式.
它们还是单项式吗?这些式子有什么共同特点?与单项式有什么关系?
单项式
单项式
+
上述几个单项式相加的形式.
a+b+c
x+21
2ar-πr2
多项式及其有关概念:
1.几个单项式的和叫做多项式;
2.在多项式中,每个单项式叫做多项式的项.
3.不含字母的项叫做常数项.
4.多项式里次数最高项的次数就是多项式的次数.
5.一个多项式含有几项,就叫做迹几项式.
总结归纳
注意:找多项式的项,必须连同前面的正负号,切记:符号不能丢哦!
多项式的次数:多项式里,次数最高项的次数,就是这个多项式的次数.
3x2-2x+5,这是___________,有______项,分别是________________,其中5是_________,3x2的次数是______,-2x的次数是_____,这个多项式的次数是________.
多项式
三
3x2 、-2x、5
常数项
2
1
2
一个多项式含有几项,就叫做几项式.
注意:确定多项式的次数时,①先找出每一项(即每一个单项式)的次数②取次数最高的.
思考:3x2-2x+5是几次几项式呢?
二次三项式.
例题讲解
解: (1)多项式 a3-a2b+ab2-b3的项有 a3、-a2b、ab2、
-b3 ,次数是 3.
(2)多项式3n4-2n2+1 的项有3n4 、-2n2 、1,次数
是4.
例1 指出下列多项式的项与次数:
(1)a3-a2b+ab2-b3;(2)3n4-2n2+1.
试一试:回答(1)中的多项式是几次几项式?
解:三次四项式.
(2)中的多项式是几次几项式呢?
例2 指出下列多项式是几次几项式:
(1) x3-x+1; (2) x3-2x2y2+3y2.
解: (1) x3-x+1是三次三项式.
(2) x3-2x2y2+3y2是四次三项式.
(2)多项式x3-2x2y2+3y2 的项有____项,分别是___________________,其中四次项的系数是_____,二次项是______,次数最高的项是_________.
三
x3、-2x2y2、3y2
-2
3y2
-2x2y2
单项式与多项式统称整式
随堂演练
1.多项式-4a2b+3ab-5的项为 ( )
A.-4a2b,3ab,5 B.-4a2b+3ab-5
C.-4a2b,3ab,-5 D.4a2b,3ab,5
2.已知一个多项式是三次二项式,则这个多项式可以是 ( )
A.x2-2x+1 B.2x3+1
C.x2-2x D.x3-2x2+1
C
B
3. 将式子:
填入相应的大括号中.
单项式:{ ,…};
多项式:{ ,…};
整式:{ ,…}.
次数:所有字母的指数的和.
系数:单项式中的数字因数.
次数:多项式中次数最高的项的次数.
整式
课堂小结
项:式中的每个单项式叫多项式的项.
(其中不含字母的项叫做常数项)
第三章 整式的加减
3.3 整式 第2课时 多项式
知识回顾
列代数式:
(1)若三角形的三条边长分别为a、b、c,则三角形
的周长是__________ ;
(2)某班有男生x人,女生21人,这个班的学生一共
有_________人;
a+b+c
(x+21)
(3)图中阴影部分的面积为___________.
列出的这些代数式有什
么共同特点 它们与单
项式有什么区别?
2ar-πr2
获取新知
几个单项式的和叫做多项式.
它们还是单项式吗?这些式子有什么共同特点?与单项式有什么关系?
单项式
单项式
+
上述几个单项式相加的形式.
a+b+c
x+21
2ar-πr2
多项式及其有关概念:
1.几个单项式的和叫做多项式;
2.在多项式中,每个单项式叫做多项式的项.
3.不含字母的项叫做常数项.
4.多项式里次数最高项的次数就是多项式的次数.
5.一个多项式含有几项,就叫做迹几项式.
总结归纳
注意:找多项式的项,必须连同前面的正负号,切记:符号不能丢哦!
多项式的次数:多项式里,次数最高项的次数,就是这个多项式的次数.
3x2-2x+5,这是___________,有______项,分别是________________,其中5是_________,3x2的次数是______,-2x的次数是_____,这个多项式的次数是________.
多项式
三
3x2 、-2x、5
常数项
2
1
2
一个多项式含有几项,就叫做几项式.
注意:确定多项式的次数时,①先找出每一项(即每一个单项式)的次数②取次数最高的.
思考:3x2-2x+5是几次几项式呢?
二次三项式.
例题讲解
解: (1)多项式 a3-a2b+ab2-b3的项有 a3、-a2b、ab2、
-b3 ,次数是 3.
(2)多项式3n4-2n2+1 的项有3n4 、-2n2 、1,次数
是4.
例1 指出下列多项式的项与次数:
(1)a3-a2b+ab2-b3;(2)3n4-2n2+1.
试一试:回答(1)中的多项式是几次几项式?
解:三次四项式.
(2)中的多项式是几次几项式呢?
例2 指出下列多项式是几次几项式:
(1) x3-x+1; (2) x3-2x2y2+3y2.
解: (1) x3-x+1是三次三项式.
(2) x3-2x2y2+3y2是四次三项式.
(2)多项式x3-2x2y2+3y2 的项有____项,分别是___________________,其中四次项的系数是_____,二次项是______,次数最高的项是_________.
三
x3、-2x2y2、3y2
-2
3y2
-2x2y2
单项式与多项式统称整式
随堂演练
1.多项式-4a2b+3ab-5的项为 ( )
A.-4a2b,3ab,5 B.-4a2b+3ab-5
C.-4a2b,3ab,-5 D.4a2b,3ab,5
2.已知一个多项式是三次二项式,则这个多项式可以是 ( )
A.x2-2x+1 B.2x3+1
C.x2-2x D.x3-2x2+1
C
B
3. 将式子:
填入相应的大括号中.
单项式:{ ,…};
多项式:{ ,…};
整式:{ ,…}.
次数:所有字母的指数的和.
系数:单项式中的数字因数.
次数:多项式中次数最高的项的次数.
整式
课堂小结
项:式中的每个单项式叫多项式的项.
(其中不含字母的项叫做常数项)
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
