华师大版数学七年级上册同步课件:4.2.2由视图到立体图形(共14张PPT)
文档属性
| 名称 | 华师大版数学七年级上册同步课件:4.2.2由视图到立体图形(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 261.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-25 19:24:26 | ||
图片预览



文档简介
(共14张PPT)
第四章 图形的初步认识
4.2 立体图形的视图
第2课时 由视图到立体图形
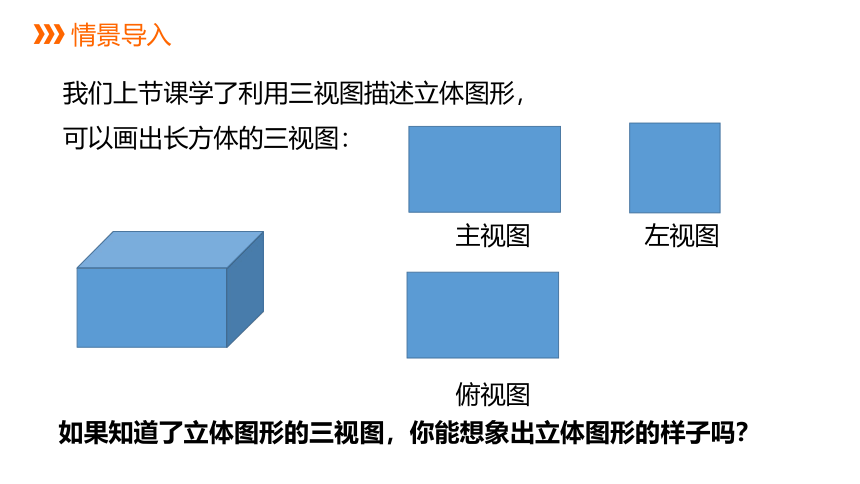
情景导入
我们上节课学了利用三视图描述立体图形,
可以画出长方体的三视图:
主视图 左视图
俯视图
如果知道了立体图形的三视图,你能想象出立体图形的样子吗?
获取新知
由三视图想象立体图形时,要先分别根据主视图、俯视图、左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
主 视 图
左 视 图
俯视图
例题讲解
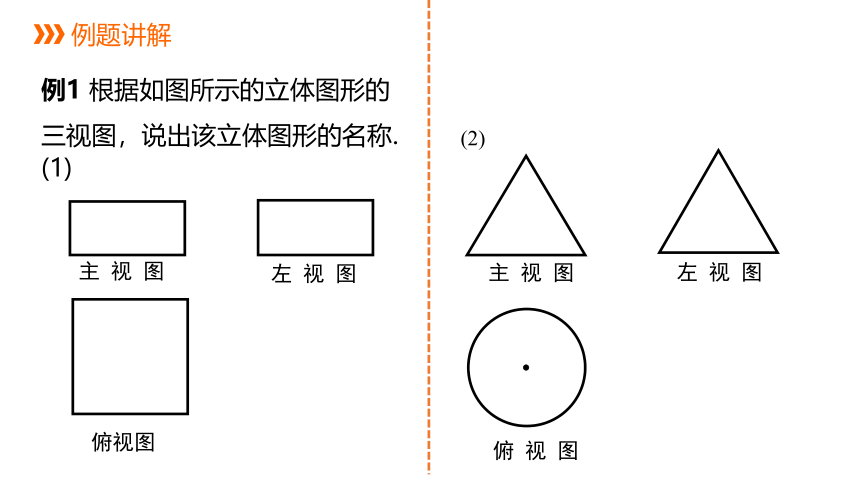
例1 根据如图所示的立体图形的三视图,说出该立体图形的名称.
(1)
俯 视 图
左 视 图
主 视 图
(2)
分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
解:(1) 从三个方向看立体图形,图形都是矩形,可以想象出:整体是长方体,如图所示.
解:(2)从正面、侧面看立体图形,图形都是等腰三角形;从上面看,图形是圆;可以想象出:整体是圆锥,如图所示.
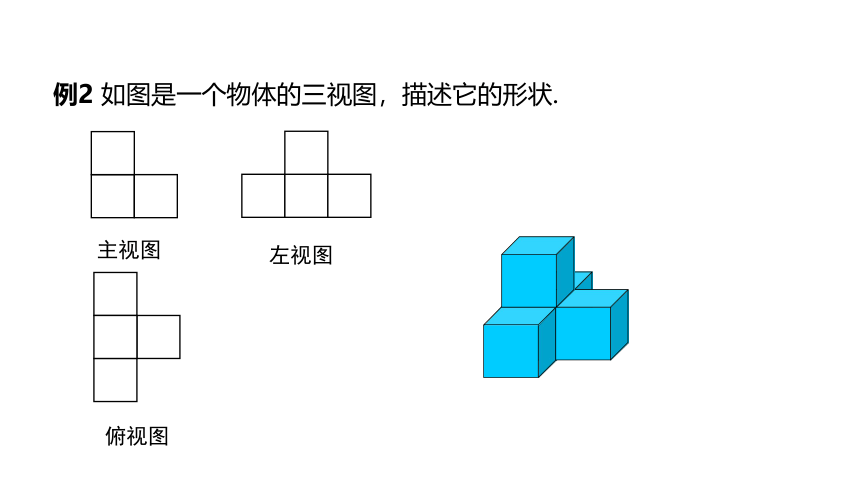
例2 如图是一个物体的三视图,描述它的形状.
主视图
左视图
俯视图
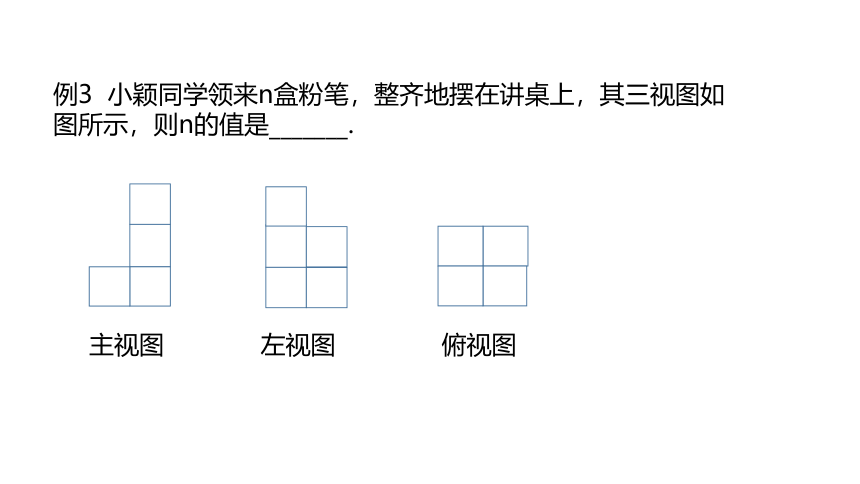
例3 小颖同学领来n盒粉笔,整齐地摆在讲桌上,其三视图如图所示,则n的值是_______.
主视图
左视图
俯视图
分析:①先根据主视图和左视图确定俯视图中每个小正方形相应位置上的小立方块的个数,②根据“去大留小”确定,③求出组成这个几何体的小立方块的个数.
1
1
3
3
1、主视图第一列有1个,第二列3个.
2、左视图第一行3个,第二行2个.
3
3
2
2
3、去大留小,将最后结果相加.
1
3
1
2
n的值是7.
例4 下列两个图是由几个相同的小正方体堆成的物体的视图,那么堆成这个物体的小正方体的个数可能是_________个.
主视图
俯视图
主视图
俯视图
分析:本题只给出了主视图和俯视图,该几何体所需小立方体的个数是不确定的,因而应充分考虑各种可能性.
解:①主视图第一列有2个,第二列1个.
2
2
1
构成这个几何体的小正方体的个数可能是4个或5个.
俯视图第一列两个小方格中,最少有3个小立方块,最多有4个立方块.
1.某立体图形的主视图和左视图如图所示,则该立体图形可能是 ( )
C
随堂演练
A.长方体 B.圆锥
C.圆柱 D.球
A
2.由四个相同的小正方体搭建了一个积木,它的三视图如图所示,
则这个积木是 ( )
3、如图是一个几何体的三视图,根据图示,该几何体的侧面积是_________
解析:从三视图可知,该几何体是圆柱,圆柱的底面直径是8,高是13,圆柱的侧面积是底面周长乘以高.
104π
课堂小结
由三视图描述几何体(或实物原型),一般步骤为:
① 想象:根据各视图想象从各个方向看到的几何体形状;
② 定形:综合确定几何体(或实物原型)的形状;
③ 定大小位置:根据三个视图“长对正,高平齐,宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸.
第四章 图形的初步认识
4.2 立体图形的视图
第2课时 由视图到立体图形
情景导入
我们上节课学了利用三视图描述立体图形,
可以画出长方体的三视图:
主视图 左视图
俯视图
如果知道了立体图形的三视图,你能想象出立体图形的样子吗?
获取新知
由三视图想象立体图形时,要先分别根据主视图、俯视图、左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
主 视 图
左 视 图
俯视图
例题讲解
例1 根据如图所示的立体图形的三视图,说出该立体图形的名称.
(1)
俯 视 图
左 视 图
主 视 图
(2)
分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
解:(1) 从三个方向看立体图形,图形都是矩形,可以想象出:整体是长方体,如图所示.
解:(2)从正面、侧面看立体图形,图形都是等腰三角形;从上面看,图形是圆;可以想象出:整体是圆锥,如图所示.
例2 如图是一个物体的三视图,描述它的形状.
主视图
左视图
俯视图
例3 小颖同学领来n盒粉笔,整齐地摆在讲桌上,其三视图如图所示,则n的值是_______.
主视图
左视图
俯视图
分析:①先根据主视图和左视图确定俯视图中每个小正方形相应位置上的小立方块的个数,②根据“去大留小”确定,③求出组成这个几何体的小立方块的个数.
1
1
3
3
1、主视图第一列有1个,第二列3个.
2、左视图第一行3个,第二行2个.
3
3
2
2
3、去大留小,将最后结果相加.
1
3
1
2
n的值是7.
例4 下列两个图是由几个相同的小正方体堆成的物体的视图,那么堆成这个物体的小正方体的个数可能是_________个.
主视图
俯视图
主视图
俯视图
分析:本题只给出了主视图和俯视图,该几何体所需小立方体的个数是不确定的,因而应充分考虑各种可能性.
解:①主视图第一列有2个,第二列1个.
2
2
1
构成这个几何体的小正方体的个数可能是4个或5个.
俯视图第一列两个小方格中,最少有3个小立方块,最多有4个立方块.
1.某立体图形的主视图和左视图如图所示,则该立体图形可能是 ( )
C
随堂演练
A.长方体 B.圆锥
C.圆柱 D.球
A
2.由四个相同的小正方体搭建了一个积木,它的三视图如图所示,
则这个积木是 ( )
3、如图是一个几何体的三视图,根据图示,该几何体的侧面积是_________
解析:从三视图可知,该几何体是圆柱,圆柱的底面直径是8,高是13,圆柱的侧面积是底面周长乘以高.
104π
课堂小结
由三视图描述几何体(或实物原型),一般步骤为:
① 想象:根据各视图想象从各个方向看到的几何体形状;
② 定形:综合确定几何体(或实物原型)的形状;
③ 定大小位置:根据三个视图“长对正,高平齐,宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
