华师大版数学七年级上册5.1.2垂线 同步课件(共19张PPT)
文档属性
| 名称 | 华师大版数学七年级上册5.1.2垂线 同步课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 06:07:36 | ||
图片预览





文档简介
(共19张PPT)
第五章 相交线和平行线
5.1.2垂线
情景导入
日常生活中,如下图中的两条直线的关系很常见,你能再举出其他例子吗?
获取新知
在相交线的模型中,固定木条a,转动木条b,
当b的位置变化时,a、b所成的角α也会发生变化.
)
α
a
b
b
b
b
b
)
α
垂线的概念
一
定义:当两条直线AB和CD所构成的四个角中有一个为直角时,其他三个角也都成为直角,此时,直线AB,CD互相垂直,记作“AB⊥CD”,其中一条直线叫做另一条直线的垂线,它们的交点 O叫做垂足.如图.
垂直的表示方法:①AB⊥CD,垂足为点O.
②AB⊥CD于点O.
两条直线垂直
相交所成的角是90°.
∵AB⊥CD
∴∠AOC=∠BOC=∠AOD=∠BOD=90°.
两条直线相交所成的角是90°
两条直线垂直
∵∠AOC=∠BOC=∠AOD=∠BOD=90°
∴AB⊥CD.
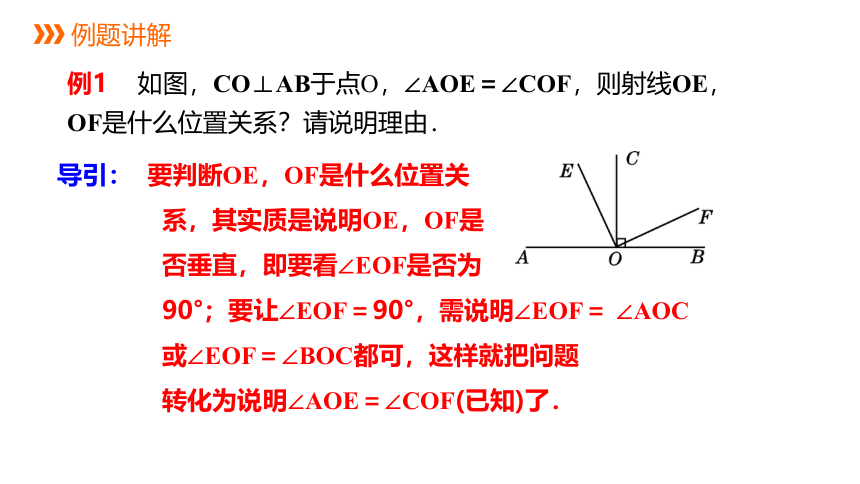
导引: 要判断OE,OF是什么位置关
系,其实质是说明OE,OF是
否垂直,即要看∠EOF是否为
90°;要让∠EOF=90°,需说明∠EOF= ∠AOC
或∠EOF=∠BOC都可,这样就把问题
转化为说明∠AOE=∠COF(已知)了.
例1 如图,CO⊥AB于点O,∠AOE=∠COF,则射线OE,OF是什么位置关系?请说明理由.
例题讲解
解:射线OE,OF互相垂直.理由如下:
因为CO⊥AB,所以∠AOC=90°.
又因为∠AOE=∠COF,
所以∠AOE+∠COE=∠COF+∠COE,
即∠AOC=∠EOF=90°.
所以OE与OF互相垂直(垂直定义).
1.放
2.靠
3.画
l
O
P·
1.经过直线l外一点P,画出垂直于l的直线,你能画出几条垂线?
【做一做】
垂线的基本事实
二
2.经过直线l上一点A,画出垂直于l的直线,你能画出几条垂线?
l
A
B
1.放
2.靠
3.移
4.画
根据以上操作,你能得出什么结论
过一点有且只有一条直线与已知直线垂直.
(1)“过一点”中的点,可以在已知直线上,也可以在已知直线外;
(2)“有且只有”中,“有”指存在,“只有”指唯一性.
注意:
垂线段及其性质
三
连接直线外一点与直线上各点的所有线段中垂线段最短.
线段AB叫做点A到直线l的垂线段;
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离
例2 如图,小鹏家在A村庄,村庄不远处有一条小河,为了把河水引入村庄,准备在河边l建一个水泵站.为了节省投资,怎样确定水泵站的位置 请在图上把最佳的位置画出来.
[解析] 根据直线外一点与直线上各点所连的线段中,垂线段最短,过点A作直线 l 的垂线,垂足即为最佳位置.
解:过点A 作AB⊥l,垂足为B,则线段AB 就是村庄A到河边的最短路线,所以水泵站的最佳位置应在点B 处.
B
垂线段最短
随堂演练
2 . 在同一平面内,下列语句正确的是( )
A.过一点有无数条直线与已知直线垂直
B.和一条直线垂直的直线有两条
C.过一点有且只有一条直线与已知直线垂直
D.两直线相交,则一定垂直
C
1 . 垂直定义的应用格式:如图,
(1)因为∠AOC=90°,所以______.
(2)因为AB⊥CD,所以∠AOC=_____°.
AB⊥CD
90
3.如图, AC⊥BC, ∠C=90° ,线段AC、BC、CD中最短的是
( )
A. AC B. BC
C. CD D. 不能确定
D
A
B
C
C
3.如图, AC⊥BC, ∠C=90° ,其中可以看作点到直线的距离的线段有( )条.
A. 3 B. 4
C. 5 D. 不能确定
D
A
B
C
C
课堂小结
知识点一 两条直线垂直的概念
定义:在两条直线相交所成的四个角中,有一个角是 时,其他三个角也都是直角,此时这两条直线互相垂直,其中一条直线是另一条直线的 ,它们的交点叫做 .
直角
垂线
垂足
知识点二 垂线的基本事实
过一点有且只有 条直线与已知直线垂直.
一
直线外
垂线段的长度
知识点三 垂线段及其性质
定义:过 一点作已知直线的垂线,这个点与垂足之间的线段叫做 ,这条 叫做这点到这条直线的距离.
性质:直线外一点与直线上各点连结所得到的所有线段中,
最短.
垂线段
垂线段
第五章 相交线和平行线
5.1.2垂线
情景导入
日常生活中,如下图中的两条直线的关系很常见,你能再举出其他例子吗?
获取新知
在相交线的模型中,固定木条a,转动木条b,
当b的位置变化时,a、b所成的角α也会发生变化.
)
α
a
b
b
b
b
b
)
α
垂线的概念
一
定义:当两条直线AB和CD所构成的四个角中有一个为直角时,其他三个角也都成为直角,此时,直线AB,CD互相垂直,记作“AB⊥CD”,其中一条直线叫做另一条直线的垂线,它们的交点 O叫做垂足.如图.
垂直的表示方法:①AB⊥CD,垂足为点O.
②AB⊥CD于点O.
两条直线垂直
相交所成的角是90°.
∵AB⊥CD
∴∠AOC=∠BOC=∠AOD=∠BOD=90°.
两条直线相交所成的角是90°
两条直线垂直
∵∠AOC=∠BOC=∠AOD=∠BOD=90°
∴AB⊥CD.
导引: 要判断OE,OF是什么位置关
系,其实质是说明OE,OF是
否垂直,即要看∠EOF是否为
90°;要让∠EOF=90°,需说明∠EOF= ∠AOC
或∠EOF=∠BOC都可,这样就把问题
转化为说明∠AOE=∠COF(已知)了.
例1 如图,CO⊥AB于点O,∠AOE=∠COF,则射线OE,OF是什么位置关系?请说明理由.
例题讲解
解:射线OE,OF互相垂直.理由如下:
因为CO⊥AB,所以∠AOC=90°.
又因为∠AOE=∠COF,
所以∠AOE+∠COE=∠COF+∠COE,
即∠AOC=∠EOF=90°.
所以OE与OF互相垂直(垂直定义).
1.放
2.靠
3.画
l
O
P·
1.经过直线l外一点P,画出垂直于l的直线,你能画出几条垂线?
【做一做】
垂线的基本事实
二
2.经过直线l上一点A,画出垂直于l的直线,你能画出几条垂线?
l
A
B
1.放
2.靠
3.移
4.画
根据以上操作,你能得出什么结论
过一点有且只有一条直线与已知直线垂直.
(1)“过一点”中的点,可以在已知直线上,也可以在已知直线外;
(2)“有且只有”中,“有”指存在,“只有”指唯一性.
注意:
垂线段及其性质
三
连接直线外一点与直线上各点的所有线段中垂线段最短.
线段AB叫做点A到直线l的垂线段;
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离
例2 如图,小鹏家在A村庄,村庄不远处有一条小河,为了把河水引入村庄,准备在河边l建一个水泵站.为了节省投资,怎样确定水泵站的位置 请在图上把最佳的位置画出来.
[解析] 根据直线外一点与直线上各点所连的线段中,垂线段最短,过点A作直线 l 的垂线,垂足即为最佳位置.
解:过点A 作AB⊥l,垂足为B,则线段AB 就是村庄A到河边的最短路线,所以水泵站的最佳位置应在点B 处.
B
垂线段最短
随堂演练
2 . 在同一平面内,下列语句正确的是( )
A.过一点有无数条直线与已知直线垂直
B.和一条直线垂直的直线有两条
C.过一点有且只有一条直线与已知直线垂直
D.两直线相交,则一定垂直
C
1 . 垂直定义的应用格式:如图,
(1)因为∠AOC=90°,所以______.
(2)因为AB⊥CD,所以∠AOC=_____°.
AB⊥CD
90
3.如图, AC⊥BC, ∠C=90° ,线段AC、BC、CD中最短的是
( )
A. AC B. BC
C. CD D. 不能确定
D
A
B
C
C
3.如图, AC⊥BC, ∠C=90° ,其中可以看作点到直线的距离的线段有( )条.
A. 3 B. 4
C. 5 D. 不能确定
D
A
B
C
C
课堂小结
知识点一 两条直线垂直的概念
定义:在两条直线相交所成的四个角中,有一个角是 时,其他三个角也都是直角,此时这两条直线互相垂直,其中一条直线是另一条直线的 ,它们的交点叫做 .
直角
垂线
垂足
知识点二 垂线的基本事实
过一点有且只有 条直线与已知直线垂直.
一
直线外
垂线段的长度
知识点三 垂线段及其性质
定义:过 一点作已知直线的垂线,这个点与垂足之间的线段叫做 ,这条 叫做这点到这条直线的距离.
性质:直线外一点与直线上各点连结所得到的所有线段中,
最短.
垂线段
垂线段
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
