华师大版数学七年级上册5.1.1对顶角 同步课件(共16张PPT)
文档属性
| 名称 | 华师大版数学七年级上册5.1.1对顶角 同步课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 06:08:59 | ||
图片预览






文档简介
(共16张PPT)
第五章 相交线与平行线
5.1.1对顶角
情景导入
观察下列图片,说一说直线与直线的位置关系.
相交
获取新知
A
B
C
D
O
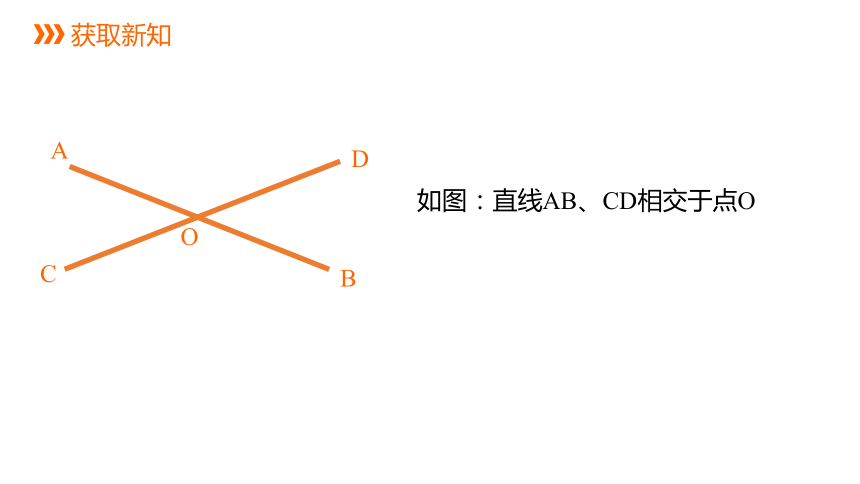
如图:直线AB、CD相交于点O
如图:两条直线相交形成了∠1、∠2、∠3、∠4.
角 ∠1和∠2 ∠2和∠3 ……
位置关系 ……
数量关系 ……
相邻
互补
相邻
互补
从位置关系与数量关系上看,图中还有哪些角之间存在某种关系呢?
定义:两个角具有相同的顶点,并且一个角的两边与另一个角的两边互为反向延长线,我们把这样的两个角叫做对顶角.如图,∠1和∠3是对顶角,∠2和∠4也是对顶角.
判断两个角是否互为对顶角的方法:
一看它们有没有公共顶点;
二看这两个角的两边是否互为反向延长线,实质就是看这两个角是否是两条直线相交所成的没有公共边的两个角.
猜想:∠1和∠3具有什么关系呢?
∠1=∠3
你会说明吗?
解:∵∠1+∠2=180°,∠3+∠2=180°
∴∠1=∠3(同角的补角相等)
对顶角相等.
例题讲解
例1 如图,两条直线相交所形成的四个角中,已知∠1=30°,那么∠2、∠3和∠4各等于多少度
解: ∵ ∠1 与∠2互补,(已知)
∴ ∠2=180°-∠1=180°-30°=150°. (互补的定义)
∵ ∠1与∠3, ∠2与∠4分别是对顶角,(已知)
∴ ∠3=∠1=30°, (对顶角相等)
∠4=∠2=150°. (对顶角相等)
对顶角的性质:对顶角相等.
请你猜一猜,剪刀剪东西的过程中,∠AOC和∠BOD这两个角的大小保持怎样的关系?
例2 如图,直线AB、CD相交于点E,∠AEC=50°,
求∠BED的度数.
解:因为直线AB、CD相交于点
E,所以∠AEC与∠BED是
对顶角.根据对顶角相等,得
∠BED =∠AEC = 50°.
随堂演练
1. 如图,∠1与∠2是对顶角的是( )
B
2.下列说法中,正确的有( )
①对顶角相等.
②相等的角是对顶角.
③不是对顶角的两个角就不相等.
④不相等的角不是对顶角.
A.1个 B.2个 C.3个 D.4个
B
3.如图,直线m,n相交于一点, ∠1+∠2=180°,∠1+∠3 =180°,则∠2=∠3的理由是 ( )
A.如果两个角的和等于90°,那么这两个角互余
B.同角(等角)的余角相等
C.如果两个角的和等于180°,那么这两个角互补
D.同角(等角)的补角相等
D
4.如图,直线AB,CD相交于点O,OA平分∠EOC,∠BOD=35°,
求∠EOC 的度数.
解:因为∠AOC与∠BOD是对顶角,
所以∠AOC=∠BOD=35°.
因为OA平分∠EOC,
所以∠EOC=2∠AOC=70°.
课堂小结
知识点一 对顶角的概念
若两角具有相同的顶点,且两角的两边互为反向延长线,则具有这种位置关系的两个角互为对顶角.
知识点二 对顶角的性质
对顶角 .
相等
第五章 相交线与平行线
5.1.1对顶角
情景导入
观察下列图片,说一说直线与直线的位置关系.
相交
获取新知
A
B
C
D
O
如图:直线AB、CD相交于点O
如图:两条直线相交形成了∠1、∠2、∠3、∠4.
角 ∠1和∠2 ∠2和∠3 ……
位置关系 ……
数量关系 ……
相邻
互补
相邻
互补
从位置关系与数量关系上看,图中还有哪些角之间存在某种关系呢?
定义:两个角具有相同的顶点,并且一个角的两边与另一个角的两边互为反向延长线,我们把这样的两个角叫做对顶角.如图,∠1和∠3是对顶角,∠2和∠4也是对顶角.
判断两个角是否互为对顶角的方法:
一看它们有没有公共顶点;
二看这两个角的两边是否互为反向延长线,实质就是看这两个角是否是两条直线相交所成的没有公共边的两个角.
猜想:∠1和∠3具有什么关系呢?
∠1=∠3
你会说明吗?
解:∵∠1+∠2=180°,∠3+∠2=180°
∴∠1=∠3(同角的补角相等)
对顶角相等.
例题讲解
例1 如图,两条直线相交所形成的四个角中,已知∠1=30°,那么∠2、∠3和∠4各等于多少度
解: ∵ ∠1 与∠2互补,(已知)
∴ ∠2=180°-∠1=180°-30°=150°. (互补的定义)
∵ ∠1与∠3, ∠2与∠4分别是对顶角,(已知)
∴ ∠3=∠1=30°, (对顶角相等)
∠4=∠2=150°. (对顶角相等)
对顶角的性质:对顶角相等.
请你猜一猜,剪刀剪东西的过程中,∠AOC和∠BOD这两个角的大小保持怎样的关系?
例2 如图,直线AB、CD相交于点E,∠AEC=50°,
求∠BED的度数.
解:因为直线AB、CD相交于点
E,所以∠AEC与∠BED是
对顶角.根据对顶角相等,得
∠BED =∠AEC = 50°.
随堂演练
1. 如图,∠1与∠2是对顶角的是( )
B
2.下列说法中,正确的有( )
①对顶角相等.
②相等的角是对顶角.
③不是对顶角的两个角就不相等.
④不相等的角不是对顶角.
A.1个 B.2个 C.3个 D.4个
B
3.如图,直线m,n相交于一点, ∠1+∠2=180°,∠1+∠3 =180°,则∠2=∠3的理由是 ( )
A.如果两个角的和等于90°,那么这两个角互余
B.同角(等角)的余角相等
C.如果两个角的和等于180°,那么这两个角互补
D.同角(等角)的补角相等
D
4.如图,直线AB,CD相交于点O,OA平分∠EOC,∠BOD=35°,
求∠EOC 的度数.
解:因为∠AOC与∠BOD是对顶角,
所以∠AOC=∠BOD=35°.
因为OA平分∠EOC,
所以∠EOC=2∠AOC=70°.
课堂小结
知识点一 对顶角的概念
若两角具有相同的顶点,且两角的两边互为反向延长线,则具有这种位置关系的两个角互为对顶角.
知识点二 对顶角的性质
对顶角 .
相等
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
