华师大版数学九年级上册23.3.2 第1课时 相似三角形判定定理1 同步课件(共16张PPT)
文档属性
| 名称 | 华师大版数学九年级上册23.3.2 第1课时 相似三角形判定定理1 同步课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 332.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
23.3.2 第1课时 相似三角形的判定定理1
第23章 图形的相似
知识回顾
我们现在判定两个三角形是否相似,必须要知道它们的对应边是否成比例,对应角是否相等.那么是否存在判定两个三角形相似的简便方法呢?
三角形全等的判定方法有哪些呢?
定义 判定方法 全等三角形
相似三角形
角边角
A
S
A
角角边
A
A
S
边边边
S
S
S
边角边
S
A
S
斜边、直角边
H
L
三角、三边对应相等的两个三角形全等
三角对应相等,三边对应成比例的两个三角形相似
获取新知
让我们先从最常见的三角尺开始.
观察你和同伴的直角三角尺,同样角度(30°与 60°,或45°与45°)
的三角尺看起来是相似的.这样从直观来看,一个三角形的三个角分别与另一个三角形的三个角对应相等时,它们就“应该”相似了.确实是这样吗?
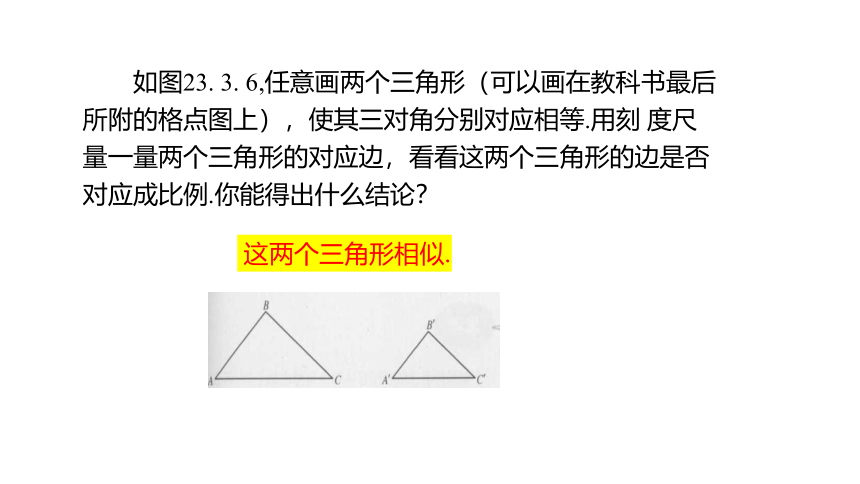
如图23. 3. 6,任意画两个三角形(可以画在教科书最后所附的格点图上),使其三对角分别对应相等.用刻 度尺量一量两个三角形的对应边,看看这两个三角形的边是否对应成比例.你能得出什么结论?
这两个三角形相似.
相似三角形的判定定理1:两角分别相等的两个三角形相似.
数学表达式:在△ABC与△A′B′C′中,
∵∠A=∠A′,∠B=∠B′,
∴△ABC∽△A′B′C′.
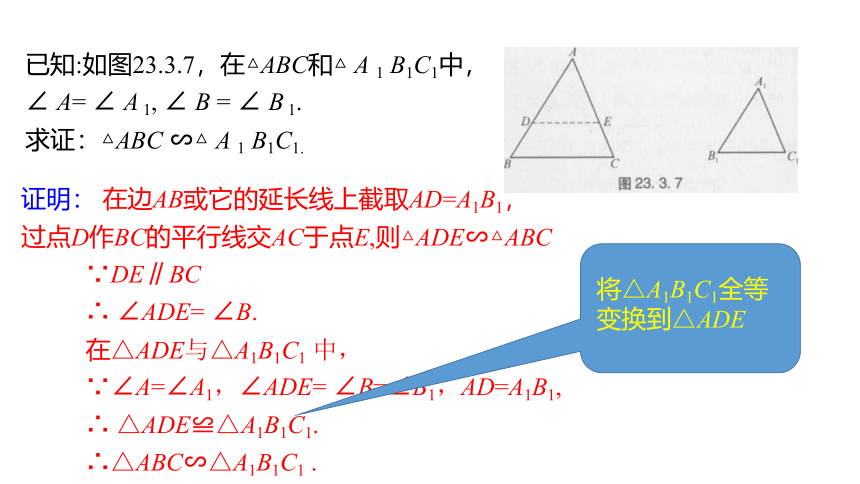
已知:如图23.3.7,在△ABC和△ A 1 B1C1中,
∠ A= ∠ A 1, ∠ B = ∠ B 1.
求证:△ABC ∽△ A 1 B1C1.
证明: 在边AB或它的延长线上截取AD=A1B1,
过点D作BC的平行线交AC于点E,则△ADE∽△ABC
∵DE∥BC
∴ ∠ADE= ∠B.
在△ADE与△A1B1C1 中,
∵∠A=∠A1,∠ADE= ∠B=∠B1,AD=A1B1,
∴ △ADE≌△A1B1C1.
∴△ABC∽△A1B1C1 .
将△A1B1C1全等变换到△ADE
例题讲解
B
例1 如图,在Rt△ABC和Rt△A ′ B ′ C ′中, ∠C 与 ∠C ′
都是直角, ∠ A = ∠ A ′ .
求证: △ABC ∽ △A ′ B ′ C ′.
推论:有一对锐角对应相等的两个直角三角形是相似的
证明:∵ ∠C= ∠C ′=90°,∠ A = ∠ A ′ ,
∴△ABC ∽ △A ′ B ′ C ′(两角分别相等的两个三角形相似).
A
B
C
D
E
F
例2 如图,在△ABC中,DE // BC,EF // AB .
求证: △ADE ∽ △EFC .
证明:∵ DE // BC,
∴∠ADE=∠B,∠AED=∠C.
又∵ EF // AB
∴ ∠EFC=∠B,
∴∠ADE=∠EFC,
∴△ADE ∽ △EFC(两角分别相等的两个三角形相似)
随堂演练
1.下列说法中错误的是( )
A.两个全等三角形一定相似
B.两个直角三角形一定相似
C.两个相似三角形的对应角相等,对应边成比例
D.相似的两个三角形不一定全等
B
随堂演练
2. 如图,已知 AB∥DE,∠AFC =∠E,则图中相似三角形共有( )
A. 1对 B. 2对 C. 3对 D. 4对
C
3.如图,D,E分别是△ABC的边AB,AC上的点,且∠ADE=∠ACB,若AD=2,AB=6,AC=4,则AE的长是( )
A.1 B.2 C.3 D.4
C
4.如图,已知P是Rt△ABC的斜边BC上任意一点,若过点P作直线PD与直角边AB或AC相交于点D,截得的小三角形与△ABC相似,则点D的位置最多有___处.
3
5.如图,∠1=∠2=∠3,求证:△ABC ∽△ADE.
证明:∵∠BAC= ∠1+ ∠DAC,
∠DAE= ∠3+ ∠DAC,∠1=∠3,
∴ ∠BAC=∠DAE.
∵ ∠C=180°-∠2-∠DOC ,
∠E=180°-∠3-∠AOE,
∠DOC =∠AOE(对顶角相等),
∴ ∠C= ∠E.
∴ △ABC∽△ADE.
A
B
C
D
E
1
3
2
O
6. 如图,为了测量一个大峡谷的宽度,地质勘探人员在对面的岩石上观察到一个明显的标志点O,再在他们所在的这一侧选点A,B,D,使得AB⊥AO,DB⊥AB,然后确定DO和AB的交点C.测得AC=120m,CB=60m,BD=50m,你能帮助他们算出峡谷的宽AO吗?
课堂小结
利用两角判定三角形相似
定理:两角分别相等的两个三角形相似
等角的寻找方法:
1.角的和与差;
2.平行线的性质;
3.对顶角相等;
4.同角(或等角)的补角(或余角)......
23.3.2 第1课时 相似三角形的判定定理1
第23章 图形的相似
知识回顾
我们现在判定两个三角形是否相似,必须要知道它们的对应边是否成比例,对应角是否相等.那么是否存在判定两个三角形相似的简便方法呢?
三角形全等的判定方法有哪些呢?
定义 判定方法 全等三角形
相似三角形
角边角
A
S
A
角角边
A
A
S
边边边
S
S
S
边角边
S
A
S
斜边、直角边
H
L
三角、三边对应相等的两个三角形全等
三角对应相等,三边对应成比例的两个三角形相似
获取新知
让我们先从最常见的三角尺开始.
观察你和同伴的直角三角尺,同样角度(30°与 60°,或45°与45°)
的三角尺看起来是相似的.这样从直观来看,一个三角形的三个角分别与另一个三角形的三个角对应相等时,它们就“应该”相似了.确实是这样吗?
如图23. 3. 6,任意画两个三角形(可以画在教科书最后所附的格点图上),使其三对角分别对应相等.用刻 度尺量一量两个三角形的对应边,看看这两个三角形的边是否对应成比例.你能得出什么结论?
这两个三角形相似.
相似三角形的判定定理1:两角分别相等的两个三角形相似.
数学表达式:在△ABC与△A′B′C′中,
∵∠A=∠A′,∠B=∠B′,
∴△ABC∽△A′B′C′.
已知:如图23.3.7,在△ABC和△ A 1 B1C1中,
∠ A= ∠ A 1, ∠ B = ∠ B 1.
求证:△ABC ∽△ A 1 B1C1.
证明: 在边AB或它的延长线上截取AD=A1B1,
过点D作BC的平行线交AC于点E,则△ADE∽△ABC
∵DE∥BC
∴ ∠ADE= ∠B.
在△ADE与△A1B1C1 中,
∵∠A=∠A1,∠ADE= ∠B=∠B1,AD=A1B1,
∴ △ADE≌△A1B1C1.
∴△ABC∽△A1B1C1 .
将△A1B1C1全等变换到△ADE
例题讲解
B
例1 如图,在Rt△ABC和Rt△A ′ B ′ C ′中, ∠C 与 ∠C ′
都是直角, ∠ A = ∠ A ′ .
求证: △ABC ∽ △A ′ B ′ C ′.
推论:有一对锐角对应相等的两个直角三角形是相似的
证明:∵ ∠C= ∠C ′=90°,∠ A = ∠ A ′ ,
∴△ABC ∽ △A ′ B ′ C ′(两角分别相等的两个三角形相似).
A
B
C
D
E
F
例2 如图,在△ABC中,DE // BC,EF // AB .
求证: △ADE ∽ △EFC .
证明:∵ DE // BC,
∴∠ADE=∠B,∠AED=∠C.
又∵ EF // AB
∴ ∠EFC=∠B,
∴∠ADE=∠EFC,
∴△ADE ∽ △EFC(两角分别相等的两个三角形相似)
随堂演练
1.下列说法中错误的是( )
A.两个全等三角形一定相似
B.两个直角三角形一定相似
C.两个相似三角形的对应角相等,对应边成比例
D.相似的两个三角形不一定全等
B
随堂演练
2. 如图,已知 AB∥DE,∠AFC =∠E,则图中相似三角形共有( )
A. 1对 B. 2对 C. 3对 D. 4对
C
3.如图,D,E分别是△ABC的边AB,AC上的点,且∠ADE=∠ACB,若AD=2,AB=6,AC=4,则AE的长是( )
A.1 B.2 C.3 D.4
C
4.如图,已知P是Rt△ABC的斜边BC上任意一点,若过点P作直线PD与直角边AB或AC相交于点D,截得的小三角形与△ABC相似,则点D的位置最多有___处.
3
5.如图,∠1=∠2=∠3,求证:△ABC ∽△ADE.
证明:∵∠BAC= ∠1+ ∠DAC,
∠DAE= ∠3+ ∠DAC,∠1=∠3,
∴ ∠BAC=∠DAE.
∵ ∠C=180°-∠2-∠DOC ,
∠E=180°-∠3-∠AOE,
∠DOC =∠AOE(对顶角相等),
∴ ∠C= ∠E.
∴ △ABC∽△ADE.
A
B
C
D
E
1
3
2
O
6. 如图,为了测量一个大峡谷的宽度,地质勘探人员在对面的岩石上观察到一个明显的标志点O,再在他们所在的这一侧选点A,B,D,使得AB⊥AO,DB⊥AB,然后确定DO和AB的交点C.测得AC=120m,CB=60m,BD=50m,你能帮助他们算出峡谷的宽AO吗?
课堂小结
利用两角判定三角形相似
定理:两角分别相等的两个三角形相似
等角的寻找方法:
1.角的和与差;
2.平行线的性质;
3.对顶角相等;
4.同角(或等角)的补角(或余角)......
