华师大版数学九年级上册23.3.3 相似三角形的性质 同步课件(共20张PPT)
文档属性
| 名称 | 华师大版数学九年级上册23.3.3 相似三角形的性质 同步课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 312.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 00:00:00 | ||
图片预览



文档简介
(共20张PPT)
23.3.3 相似三角形的性质
第23章 图形的相似
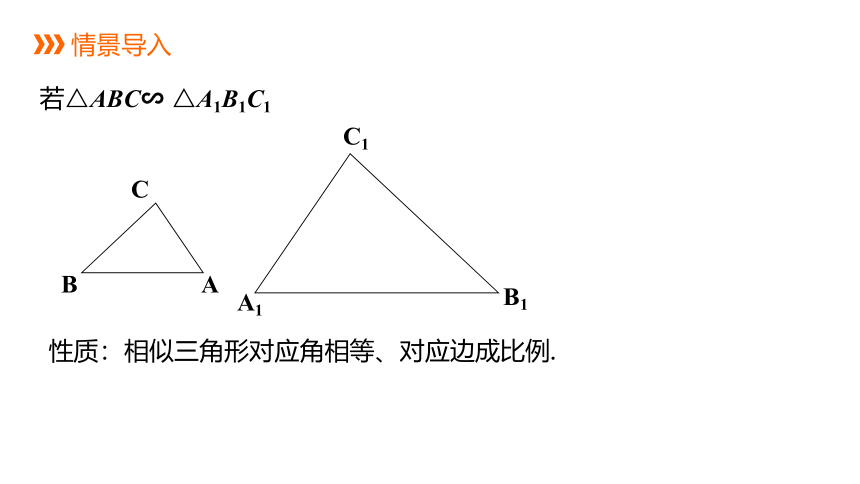
情景导入
A
C
B
A1
C1
B1
性质:相似三角形对应角相等、对应边成比例.
若△ABC∽ △A1B1C1
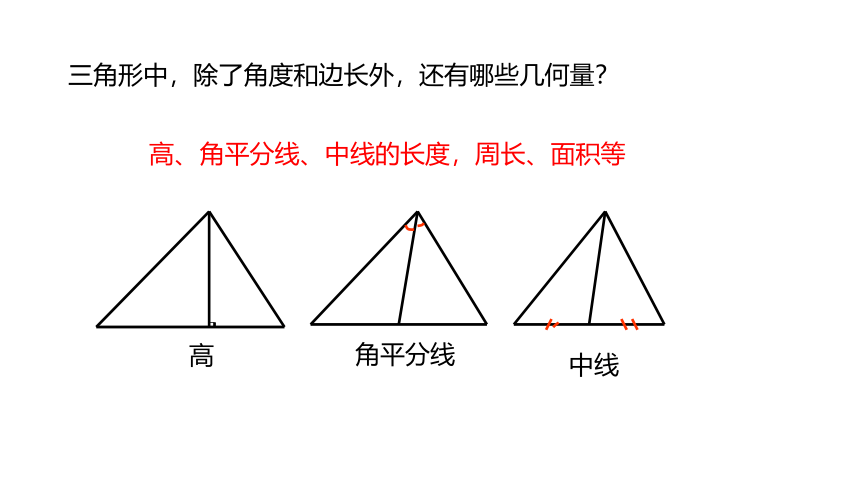
三角形中,除了角度和边长外,还有哪些几何量?
高、角平分线、中线的长度,周长、面积等
高
角平分线
中线
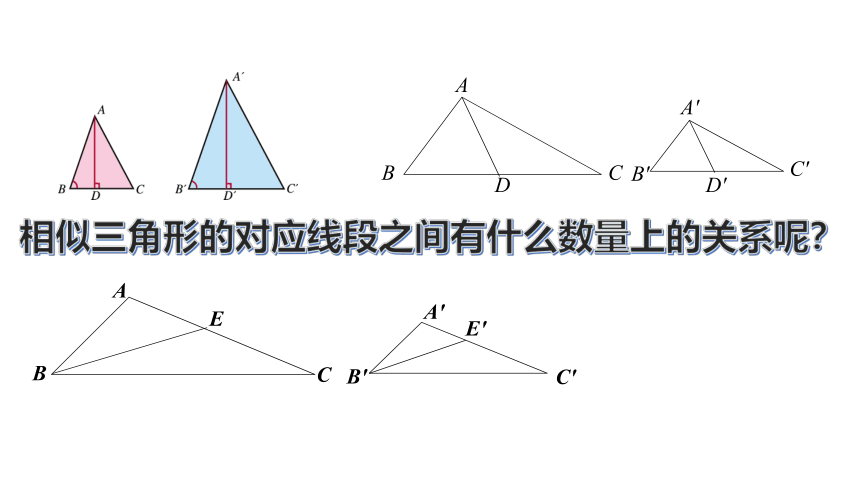
A'
B'
D'
C'
A
B
C
D
A'
B'
C'
E'
A
B
C
E
相似三角形的对应线段之间有什么数量上的关系呢?
获取新知
△ABD和△A'B ' D'都是直角三角形,且∠B=∠B',因为有两个角对应相等,所以这两个三角形相似. 因此
结论1.相似三角形对应边上的高的比等于相似比
一、相似三角形对应边上的高的比等于相似比
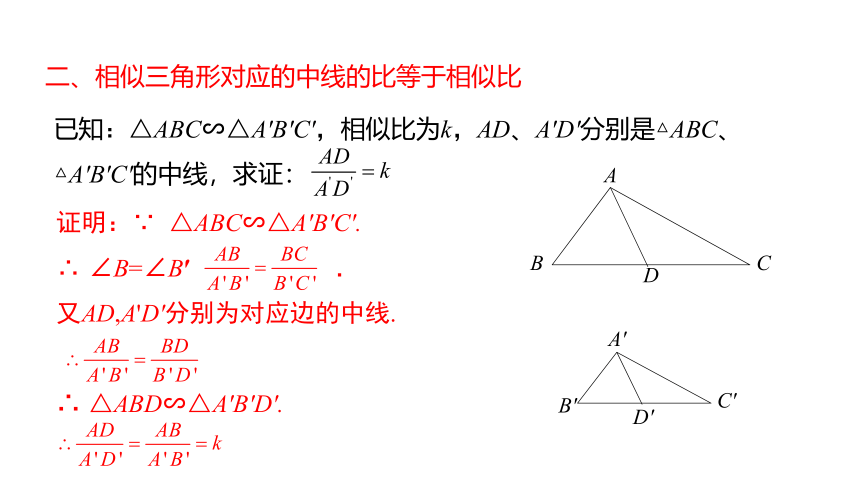
二、相似三角形对应的中线的比等于相似比
已知:△ABC∽△A′B′C′,相似比为k,AD、A′D′分别是△ABC、△A′B′C′的中线,求证:
证明:∵ △ABC∽△A′B′C′.
∴ ∠B=∠B′ .
又AD,A'D′分别为对应边的中线.
∴ △ABD∽△A′B′D′.
A'
B'
D'
C'
A
B
C
D
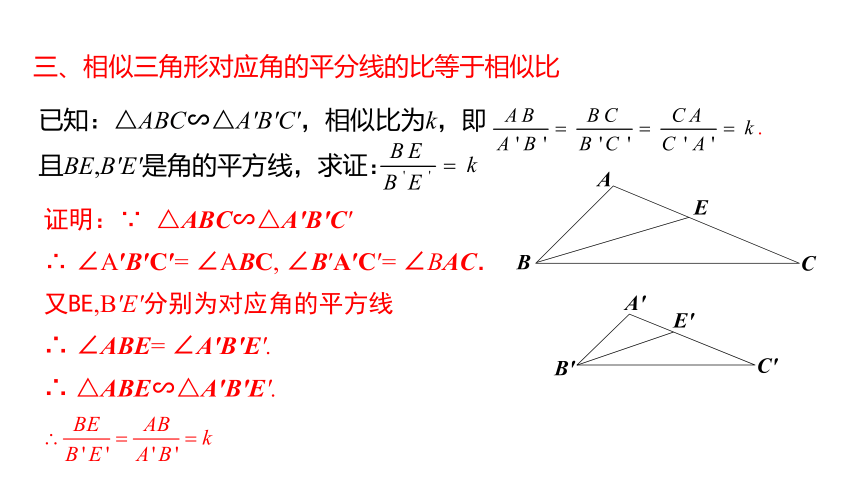
三、相似三角形对应角的平分线的比等于相似比
A'
B'
C'
E'
A
B
C
E
已知:△ABC∽△A′B′C′,相似比为k,即
且BE,B′E′是角的平方线,求证:
证明:∵ △ABC∽△A′B′C′
∴ ∠A′B′C′= ∠ABC, ∠B′A′C′= ∠BAC.
又BE,B′E′分别为对应角的平方线
∴ ∠ABE= ∠A′B′E′.
∴ △ABE∽△A′B′E′.
四、相似三角形周长的比等于相似比
证明:设△ABC∽△A1B1C1,相似比为k,
求证:相似三角形的周长比等于相似比.
A
B
C
A1
B1
C1
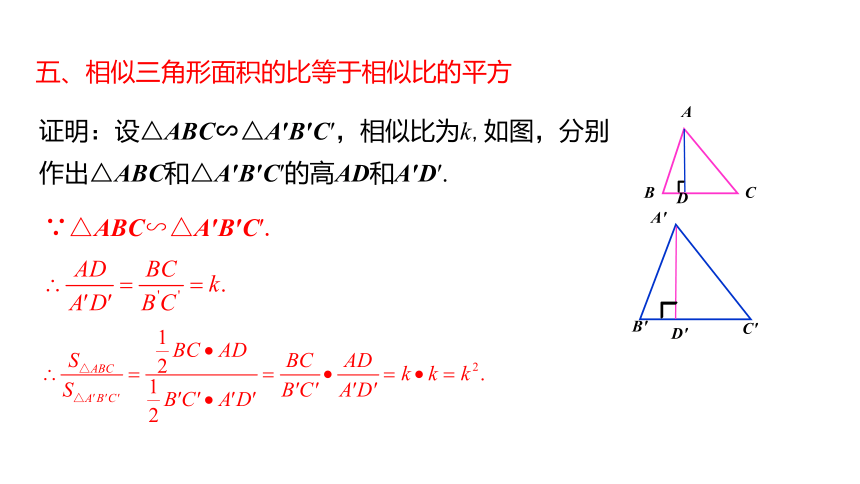
五、相似三角形面积的比等于相似比的平方
证明:设△ABC∽△A′B′C′,相似比为k,如图,分别作出△ABC和△A′B′C′的高AD和A′D′.
∵△ABC∽△A′B′C′.
A
B
C
A′
B′
C′
D
D′
1. 相似三角形对应边上的高的比等于相似比.
2. 相似三角形对应边上的中线的比等于相似比.
3. 相似三角形对应角的平分线的比等于相似比.
4. 相似三角形的周长之比等于相似比;
5.相似三角形面积的比等于相似比的平方;
易错警示:利用相似三角形的性质时,
要注意“对应”两字,要找准对应线段.
例题讲解
例1 如图,AD是△ABC的高,AD=h,点R在AC边上,点S在AB边上,SR⊥AD,垂足为E.
当SR= BC时,求DE的长.如果SR= BC呢?
解:∵ SR⊥AD, BC⊥AD,∴ SR∥BC.
∴ ∠ASR=∠B, ∠ARS=∠C.
∴ △ASR∽△ ABC(两角分别相等的两个三角形相似).
(相似三角形对应高的比等于相似比),
当SR= BC时,得 解得DE= h.
当SR= BC时,得 解得DE= h.
例2 已知:如图,□ ABCD中,E是BC边上一点,且BE= EC,BD,AE相交于F点.
(1)求△BEF的周长与△AFD的周长之比;
(2)若△BEF的面积为6 cm2,求△AFD的面积.
解:(1)∵四边形ABCD是平行四边形,
∴BC∥AD,BC=AD.
∴△BEF∽△DAF.
∵BE= EC,
∴BE∶DA=BE∶BC=1∶3.
∴△BEF的周长与△AFD的周长之比为1∶3.
(2)由(1)可知△BEF与△AFD的相似比为
∴S△BEF∶S△AFD=1∶9.
又∵S△BEF=6 cm2,∴S△AFD=54 cm2.
随堂演练
1.如果两个相似三角形对应边的比为2∶3,那么这两个相似三角形面积的比是( )
A.2∶3 B.
C.4∶9 D.8∶27
C
2.如图,△ABC∽△A′B′C′,AD,BE分别是△ABC的高和中线,A′D′,B′E′分别是△A′B′C′的高和中线,且AD=4,A′D′=3,BE=6,则B′E′的长为( )
D
3.如图是一个照相机成像的示意图,如果底片AB宽40 mm,焦距是60 mm,求所拍摄的2 m外景物的宽CD.
解:由题意,可知△ABE∽△DCE,
答:所拍摄的2 m外景物的宽CD为
4.已知△ABC∽△A'B'C', ,AB边上的中线CD=4cm,
△ABC的周长为20cm,△A'B'C'的面积为64 cm2,求:
(1)A'B'边上的中线C'D'的长;
(2)△A'B'C'的周长;
(3)△ABC的面积.
课堂小结
相似三角形的性质
相似三角形对应线段的比等于相似比(高、中线、角平分线)
相似三角形周长比等于相似比
相似三角形面积的比等于相似比的平方(反之,为算术平方根)
23.3.3 相似三角形的性质
第23章 图形的相似
情景导入
A
C
B
A1
C1
B1
性质:相似三角形对应角相等、对应边成比例.
若△ABC∽ △A1B1C1
三角形中,除了角度和边长外,还有哪些几何量?
高、角平分线、中线的长度,周长、面积等
高
角平分线
中线
A'
B'
D'
C'
A
B
C
D
A'
B'
C'
E'
A
B
C
E
相似三角形的对应线段之间有什么数量上的关系呢?
获取新知
△ABD和△A'B ' D'都是直角三角形,且∠B=∠B',因为有两个角对应相等,所以这两个三角形相似. 因此
结论1.相似三角形对应边上的高的比等于相似比
一、相似三角形对应边上的高的比等于相似比
二、相似三角形对应的中线的比等于相似比
已知:△ABC∽△A′B′C′,相似比为k,AD、A′D′分别是△ABC、△A′B′C′的中线,求证:
证明:∵ △ABC∽△A′B′C′.
∴ ∠B=∠B′ .
又AD,A'D′分别为对应边的中线.
∴ △ABD∽△A′B′D′.
A'
B'
D'
C'
A
B
C
D
三、相似三角形对应角的平分线的比等于相似比
A'
B'
C'
E'
A
B
C
E
已知:△ABC∽△A′B′C′,相似比为k,即
且BE,B′E′是角的平方线,求证:
证明:∵ △ABC∽△A′B′C′
∴ ∠A′B′C′= ∠ABC, ∠B′A′C′= ∠BAC.
又BE,B′E′分别为对应角的平方线
∴ ∠ABE= ∠A′B′E′.
∴ △ABE∽△A′B′E′.
四、相似三角形周长的比等于相似比
证明:设△ABC∽△A1B1C1,相似比为k,
求证:相似三角形的周长比等于相似比.
A
B
C
A1
B1
C1
五、相似三角形面积的比等于相似比的平方
证明:设△ABC∽△A′B′C′,相似比为k,如图,分别作出△ABC和△A′B′C′的高AD和A′D′.
∵△ABC∽△A′B′C′.
A
B
C
A′
B′
C′
D
D′
1. 相似三角形对应边上的高的比等于相似比.
2. 相似三角形对应边上的中线的比等于相似比.
3. 相似三角形对应角的平分线的比等于相似比.
4. 相似三角形的周长之比等于相似比;
5.相似三角形面积的比等于相似比的平方;
易错警示:利用相似三角形的性质时,
要注意“对应”两字,要找准对应线段.
例题讲解
例1 如图,AD是△ABC的高,AD=h,点R在AC边上,点S在AB边上,SR⊥AD,垂足为E.
当SR= BC时,求DE的长.如果SR= BC呢?
解:∵ SR⊥AD, BC⊥AD,∴ SR∥BC.
∴ ∠ASR=∠B, ∠ARS=∠C.
∴ △ASR∽△ ABC(两角分别相等的两个三角形相似).
(相似三角形对应高的比等于相似比),
当SR= BC时,得 解得DE= h.
当SR= BC时,得 解得DE= h.
例2 已知:如图,□ ABCD中,E是BC边上一点,且BE= EC,BD,AE相交于F点.
(1)求△BEF的周长与△AFD的周长之比;
(2)若△BEF的面积为6 cm2,求△AFD的面积.
解:(1)∵四边形ABCD是平行四边形,
∴BC∥AD,BC=AD.
∴△BEF∽△DAF.
∵BE= EC,
∴BE∶DA=BE∶BC=1∶3.
∴△BEF的周长与△AFD的周长之比为1∶3.
(2)由(1)可知△BEF与△AFD的相似比为
∴S△BEF∶S△AFD=1∶9.
又∵S△BEF=6 cm2,∴S△AFD=54 cm2.
随堂演练
1.如果两个相似三角形对应边的比为2∶3,那么这两个相似三角形面积的比是( )
A.2∶3 B.
C.4∶9 D.8∶27
C
2.如图,△ABC∽△A′B′C′,AD,BE分别是△ABC的高和中线,A′D′,B′E′分别是△A′B′C′的高和中线,且AD=4,A′D′=3,BE=6,则B′E′的长为( )
D
3.如图是一个照相机成像的示意图,如果底片AB宽40 mm,焦距是60 mm,求所拍摄的2 m外景物的宽CD.
解:由题意,可知△ABE∽△DCE,
答:所拍摄的2 m外景物的宽CD为
4.已知△ABC∽△A'B'C', ,AB边上的中线CD=4cm,
△ABC的周长为20cm,△A'B'C'的面积为64 cm2,求:
(1)A'B'边上的中线C'D'的长;
(2)△A'B'C'的周长;
(3)△ABC的面积.
课堂小结
相似三角形的性质
相似三角形对应线段的比等于相似比(高、中线、角平分线)
相似三角形周长比等于相似比
相似三角形面积的比等于相似比的平方(反之,为算术平方根)
