华师大版数学九年级上册23.4 中位线 同步课件(共17张PPT)
文档属性
| 名称 | 华师大版数学九年级上册23.4 中位线 同步课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 268.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 06:23:46 | ||
图片预览






文档简介
(共17张PPT)
23.4 中位线
第23章 图形的相似
情景导入
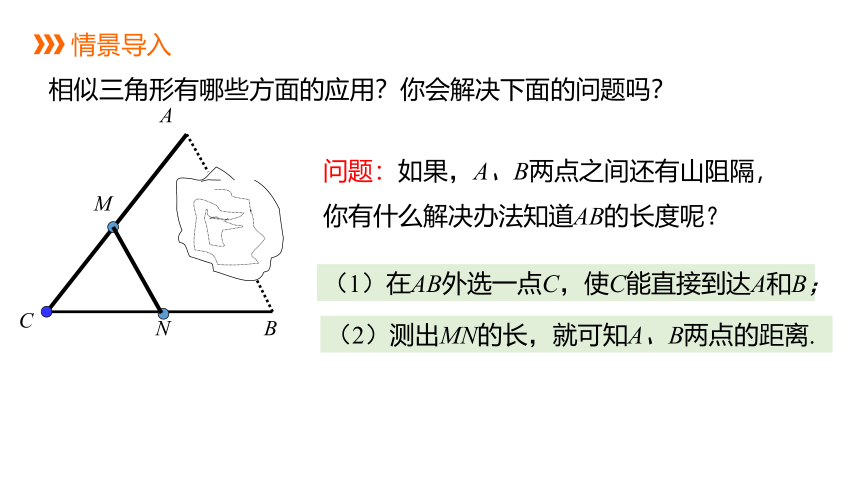
相似三角形有哪些方面的应用?你会解决下面的问题吗?
A
B
(2)测出MN的长,就可知A、B两点的距离.
M
N
(1)在AB外选一点C,使C能直接到达A和B;
C
问题:如果,A、B两点之间还有山阻隔,你有什么解决办法知道AB的长度呢?
在23.3节中,我们曾得到如下结论:
A
DE//BC
△ADE∽△ABC
D是AB的中点
E也是AC的中点
D是AB的中点
E也是AC的中点
DE//BC
获取新知
中线:连结顶点与对边中点的线段
中位线:连结三角形两边中点的线段
A
B
C
E
F
.
.
中位线
D
中线
猜想
如图,在△ABC中,点D、E分别是
AB与AC 的中点.根据画出的图形,
可以猜想:
DE // BC,且DE = BC.
对此,我们可以用演绎推理给出证明.
C
证明:在△ABC中,
∵点D、E分别是AB与AC的中点,
∴
∵∠A=∠A,
∴△ADE∽△ABC,
∵∠ADE = ∠ABC,
∴
C
三角形中位线的性质
三角形的中位线平行于第三边,并且等于它的一半.
符号语言
D
A
B
C
E
∵DE是△ABC的中位线
∴ DE∥BC,
DE= BC.
例题讲解
例1 求证:三角形的一条中位线与第三边上的中线互相平分. 已知:如图, 在 △ABC 中,AD =DB,BE=EC, AF = FC.
求证:AE、DF互相平分.
证明:连结DE、EF.
∵AD = DB,BE = EC,
∴DE//AC(三角形的中位线平行于第三边,并且等于第三边的一半).
同理可得EF//BA.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分.
D
A
B
C
F
E
例2 如图,在△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于点G. 求证:
证明:连结ED.
∵D、E分别是边BC、AB的中点,
∴DE//AC , (三角形的中位线平行于第
三边,并且等于第三边的一半).
∴△ACG∽△DEG,
∴
E
A
B
C
D
G
B
C
D
F
G`
A
G`
三角形的重心的定义:三角形的重心是三角形三
条中线的交点.
三角形重心的性质:三角形的重心与一边中点的
连线的长是对应中线长的
如果在上图中,取AC的中点F,假设BF与AD交于G',如下图,那么我们同理有,
所以有 ,即两图中的点G与G'是重合的.
于是我们有以下结论:
随堂演练
1.如图是一块等腰三角形空地ABC,已知D,E分别是边AB,AC的中点,量得AC=10米,AB=BC=6米.若用篱笆围成四边形BCED来放养小鸡,则需要篱笆的长是( )
A.22米 B.17米 C.14米 D.11米
B
2.如图所示,已知点E、F分别是△ABC的边AC、AB的中点,BE、CF相交于点G,FG=1,则CF的长为( )
A.2 B.1.5 C.3 D.4
C
3.如图所示,在△ABC中,G为重心,连结AG并延长,交边BC于点D,若△ABC的面积为6 cm2,则△BGD的面积为_______.
1cm2
4.在△ABC中,中线CE、BF相交点O、M、N分别是OB、OC的中点,
则EF和MN的关系是_______________.
平行且相等
5.求证:顺次连结四边形四条边的中点所得的四边形是平行四边形.
已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
证明:连结AC.
∵AH=HD,CG=GD ,
∴HG∥AC, HG= AC.
同理 EF∥AC, EF= AC,
∴HG∥EF ,HG=EF.
∴四边形EFGH是平行四边形.
1. 中点四边形:顺次连结四边形各边中点所得的四边形叫做中点四边形.
2.常见的中点四边形:
(1) 顺次连结任意四边形各边中点所得的四边形是平行四边形;
(2) 顺次连结矩形各边中点所得的四边形是菱形;
(3) 顺次连结菱形各边中点所得的四边形是矩形;
(4) 顺次连结正方形各边中点所得的四边形是正方形;
(5) 顺次连结等腰梯形各边中点所得的四边形是菱形.
课堂小结
1.三角形的中位线定义:连结三角形两边中点的线段叫做三角形的中位线.
2.三角形的中位线性质:三角形的中位线平行于第三边,并且等于它的一半.
3.三角形的中位线性质不仅给出了中位线与第三边的关系,而且给出了它们的数量关系,在三角形中给出一边的中点时,可转化为中位线.(见中点作中位线)
23.4 中位线
第23章 图形的相似
情景导入
相似三角形有哪些方面的应用?你会解决下面的问题吗?
A
B
(2)测出MN的长,就可知A、B两点的距离.
M
N
(1)在AB外选一点C,使C能直接到达A和B;
C
问题:如果,A、B两点之间还有山阻隔,你有什么解决办法知道AB的长度呢?
在23.3节中,我们曾得到如下结论:
A
DE//BC
△ADE∽△ABC
D是AB的中点
E也是AC的中点
D是AB的中点
E也是AC的中点
DE//BC
获取新知
中线:连结顶点与对边中点的线段
中位线:连结三角形两边中点的线段
A
B
C
E
F
.
.
中位线
D
中线
猜想
如图,在△ABC中,点D、E分别是
AB与AC 的中点.根据画出的图形,
可以猜想:
DE // BC,且DE = BC.
对此,我们可以用演绎推理给出证明.
C
证明:在△ABC中,
∵点D、E分别是AB与AC的中点,
∴
∵∠A=∠A,
∴△ADE∽△ABC,
∵∠ADE = ∠ABC,
∴
C
三角形中位线的性质
三角形的中位线平行于第三边,并且等于它的一半.
符号语言
D
A
B
C
E
∵DE是△ABC的中位线
∴ DE∥BC,
DE= BC.
例题讲解
例1 求证:三角形的一条中位线与第三边上的中线互相平分. 已知:如图, 在 △ABC 中,AD =DB,BE=EC, AF = FC.
求证:AE、DF互相平分.
证明:连结DE、EF.
∵AD = DB,BE = EC,
∴DE//AC(三角形的中位线平行于第三边,并且等于第三边的一半).
同理可得EF//BA.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分.
D
A
B
C
F
E
例2 如图,在△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于点G. 求证:
证明:连结ED.
∵D、E分别是边BC、AB的中点,
∴DE//AC , (三角形的中位线平行于第
三边,并且等于第三边的一半).
∴△ACG∽△DEG,
∴
E
A
B
C
D
G
B
C
D
F
G`
A
G`
三角形的重心的定义:三角形的重心是三角形三
条中线的交点.
三角形重心的性质:三角形的重心与一边中点的
连线的长是对应中线长的
如果在上图中,取AC的中点F,假设BF与AD交于G',如下图,那么我们同理有,
所以有 ,即两图中的点G与G'是重合的.
于是我们有以下结论:
随堂演练
1.如图是一块等腰三角形空地ABC,已知D,E分别是边AB,AC的中点,量得AC=10米,AB=BC=6米.若用篱笆围成四边形BCED来放养小鸡,则需要篱笆的长是( )
A.22米 B.17米 C.14米 D.11米
B
2.如图所示,已知点E、F分别是△ABC的边AC、AB的中点,BE、CF相交于点G,FG=1,则CF的长为( )
A.2 B.1.5 C.3 D.4
C
3.如图所示,在△ABC中,G为重心,连结AG并延长,交边BC于点D,若△ABC的面积为6 cm2,则△BGD的面积为_______.
1cm2
4.在△ABC中,中线CE、BF相交点O、M、N分别是OB、OC的中点,
则EF和MN的关系是_______________.
平行且相等
5.求证:顺次连结四边形四条边的中点所得的四边形是平行四边形.
已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
证明:连结AC.
∵AH=HD,CG=GD ,
∴HG∥AC, HG= AC.
同理 EF∥AC, EF= AC,
∴HG∥EF ,HG=EF.
∴四边形EFGH是平行四边形.
1. 中点四边形:顺次连结四边形各边中点所得的四边形叫做中点四边形.
2.常见的中点四边形:
(1) 顺次连结任意四边形各边中点所得的四边形是平行四边形;
(2) 顺次连结矩形各边中点所得的四边形是菱形;
(3) 顺次连结菱形各边中点所得的四边形是矩形;
(4) 顺次连结正方形各边中点所得的四边形是正方形;
(5) 顺次连结等腰梯形各边中点所得的四边形是菱形.
课堂小结
1.三角形的中位线定义:连结三角形两边中点的线段叫做三角形的中位线.
2.三角形的中位线性质:三角形的中位线平行于第三边,并且等于它的一半.
3.三角形的中位线性质不仅给出了中位线与第三边的关系,而且给出了它们的数量关系,在三角形中给出一边的中点时,可转化为中位线.(见中点作中位线)
