华师大版数学九年级上册24.2 直角三角形的性质 同步课件(共16张PPT)
文档属性
| 名称 | 华师大版数学九年级上册24.2 直角三角形的性质 同步课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 215.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
24.2 直角三角形的性质
第24章 解直角三角形
知识回顾
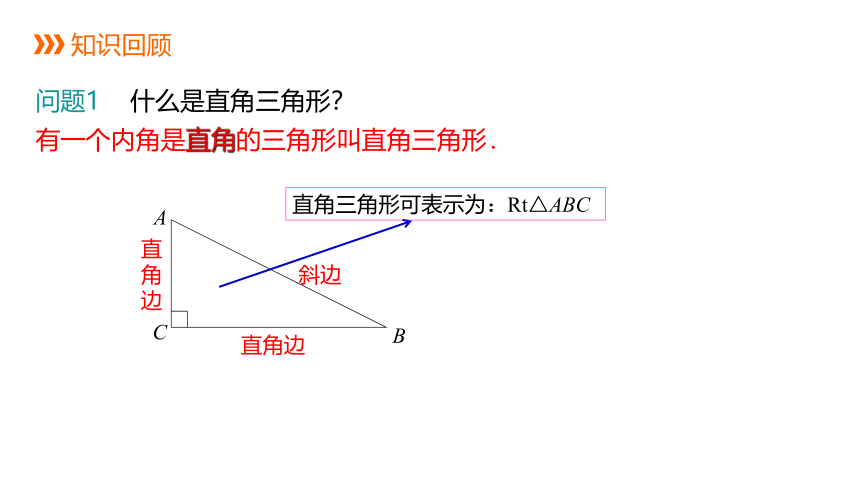
问题1 什么是直角三角形?
有一个内角是直角的三角形叫直角三角形.
直角三角形可表示为:Rt△ABC
A
C
B
斜边
直角边
直角边
(1)直角三角形的两个锐角________;
互余
(2)勾股定理:直角三角形两直角边的平方和______斜边的平方.
等于
问题2 你知道我们学过了直角三角形的哪些性质?
下面我们探索直角三角形的其他性质
获取新知
如图,画Rt△ABC,并画出斜边AB上的中线CD量一量,看看CD与AB有什么关系.
知识点一:直角三角形的性质3
A
B
C
┐
D
猜想:CD恰好是AB的一半
A
B
C
┐
D
E
已知:如图 ,在 Rt ABC 中, ∠ ACB= 90 °, CD是斜边AB上的中线. 求证:CD = AB
证明:延长CD至点E,使DE= CD,连结AE、BE
∵CD是斜边AB上的中线,
∴AD = DB.
又∵ DE = CD,
∴四边形ACBE是平行四边形.
又∵∠ACB=90°,
∴四边形ACBE是矩形,
∴ CE = AB,
∴ CD = CE = AB.
直角三角形的性质之(3)
在直角三角形中,斜边上的中线等于斜边的一半.
符号语言为:
在Rt△ABC中
∵CD是斜边AB上的中线,
∴CD=AD=BD= AB.
(直角三角形斜边上的中线等于斜边的一半)
A
B
C
┐
D
例题讲解
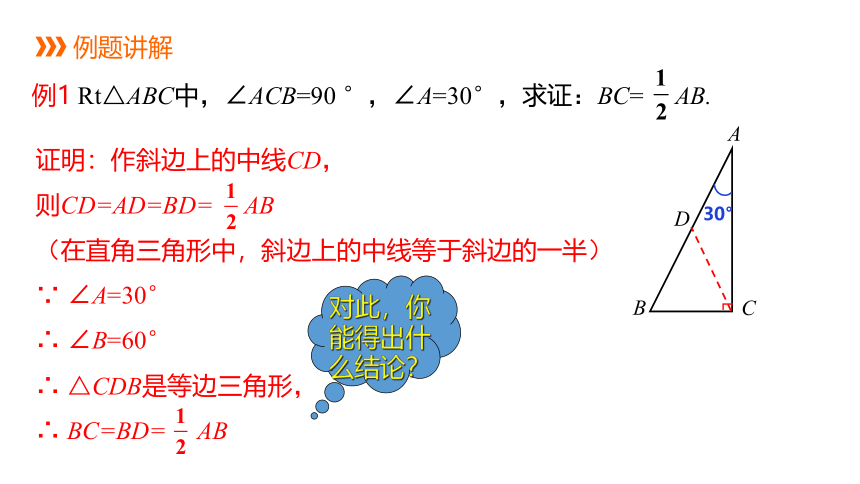
例1 Rt△ABC中,∠ACB=90 °,∠A=30°,求证:BC= AB.
A
B
C
┐
D
证明:作斜边上的中线CD,
则CD=AD=BD= AB
(在直角三角形中,斜边上的中线等于斜边的一半)
∵ ∠A=30°
∴ ∠B=60°
∴ △CDB是等边三角形,
∴ BC=BD= AB
对此,你能得出什么结论?
30°
获取新知
知识点二:直角三角形的性质4
直角三角形的性质之(4)
在直角三角形中,30°所对的直角边等于斜边的一半
符号语言为:
在Rt△ABC中
∵∠A=30°,
∴BC= AB.
(直角三角形斜30°所对的直角边等于斜边的一半)
A
B
C
┐
30°
例题讲解
例2 如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=15°,然后朝着旗杆方向前进到点D,测得∠ADB=30°,量得CD=13 m,求旗杆AB的高度.
A
B
C
D
A
B
C
D
解: ∵∠ACB=15°,∠ADB=30°,
∴∠CAD=∠ADB-∠ACB=30°-15°=15°,
∴∠ACB=∠CAD,∴AD=CD=13 m.
在△ADB中,
∵AB⊥DB,∠ADB=30°,
随堂演练
1.如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连结DE,则△CDE的周长为( )
A.20 B.12 C.14 D.13
C
2.如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( )
A.6 B.6 C.9 D.3
C
3.在直角三角形中,斜边及其中线之和为6,那么该三角形的斜边长为____
4顶角为30度的等腰三角形,若腰长为2,则腰上的高_____,三角形面积是____
4
5.如图,在△ABC中,∠B=∠C,D、E分别是BC、AC的中点,AB=6,求DE的长。
解:∵∠B=∠C
∴AB=AC=6
∵D是BC的中点
∴AD⊥BC
∵E是AC的中点
∴DE= AC=3
6.如图,△ABC中,∠C=90°,∠A=60 °,EF是AB的垂直平分线,判断CE与BE之间的关系
解:结论:CE= BE,连接AE
∵∠C=90°,∠A=60 °∴∠B=30°
∵EF是AB的垂直平分线,∴BE=AE
∴∠B=∠BAE=30°
∴∠BAE=30°
∴CE= AE
∴CE= BE
课堂小结
我们学习了直角三角形哪些性质?
性质1
直角三角形两个锐角互余
性质2
直角三角形的勾股定理
性质3
直角三角形斜边上的中线等于斜边的一半
性质4
直角三角形30 角所对直角边等于斜边的一半
24.2 直角三角形的性质
第24章 解直角三角形
知识回顾
问题1 什么是直角三角形?
有一个内角是直角的三角形叫直角三角形.
直角三角形可表示为:Rt△ABC
A
C
B
斜边
直角边
直角边
(1)直角三角形的两个锐角________;
互余
(2)勾股定理:直角三角形两直角边的平方和______斜边的平方.
等于
问题2 你知道我们学过了直角三角形的哪些性质?
下面我们探索直角三角形的其他性质
获取新知
如图,画Rt△ABC,并画出斜边AB上的中线CD量一量,看看CD与AB有什么关系.
知识点一:直角三角形的性质3
A
B
C
┐
D
猜想:CD恰好是AB的一半
A
B
C
┐
D
E
已知:如图 ,在 Rt ABC 中, ∠ ACB= 90 °, CD是斜边AB上的中线. 求证:CD = AB
证明:延长CD至点E,使DE= CD,连结AE、BE
∵CD是斜边AB上的中线,
∴AD = DB.
又∵ DE = CD,
∴四边形ACBE是平行四边形.
又∵∠ACB=90°,
∴四边形ACBE是矩形,
∴ CE = AB,
∴ CD = CE = AB.
直角三角形的性质之(3)
在直角三角形中,斜边上的中线等于斜边的一半.
符号语言为:
在Rt△ABC中
∵CD是斜边AB上的中线,
∴CD=AD=BD= AB.
(直角三角形斜边上的中线等于斜边的一半)
A
B
C
┐
D
例题讲解
例1 Rt△ABC中,∠ACB=90 °,∠A=30°,求证:BC= AB.
A
B
C
┐
D
证明:作斜边上的中线CD,
则CD=AD=BD= AB
(在直角三角形中,斜边上的中线等于斜边的一半)
∵ ∠A=30°
∴ ∠B=60°
∴ △CDB是等边三角形,
∴ BC=BD= AB
对此,你能得出什么结论?
30°
获取新知
知识点二:直角三角形的性质4
直角三角形的性质之(4)
在直角三角形中,30°所对的直角边等于斜边的一半
符号语言为:
在Rt△ABC中
∵∠A=30°,
∴BC= AB.
(直角三角形斜30°所对的直角边等于斜边的一半)
A
B
C
┐
30°
例题讲解
例2 如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=15°,然后朝着旗杆方向前进到点D,测得∠ADB=30°,量得CD=13 m,求旗杆AB的高度.
A
B
C
D
A
B
C
D
解: ∵∠ACB=15°,∠ADB=30°,
∴∠CAD=∠ADB-∠ACB=30°-15°=15°,
∴∠ACB=∠CAD,∴AD=CD=13 m.
在△ADB中,
∵AB⊥DB,∠ADB=30°,
随堂演练
1.如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连结DE,则△CDE的周长为( )
A.20 B.12 C.14 D.13
C
2.如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( )
A.6 B.6 C.9 D.3
C
3.在直角三角形中,斜边及其中线之和为6,那么该三角形的斜边长为____
4顶角为30度的等腰三角形,若腰长为2,则腰上的高_____,三角形面积是____
4
5.如图,在△ABC中,∠B=∠C,D、E分别是BC、AC的中点,AB=6,求DE的长。
解:∵∠B=∠C
∴AB=AC=6
∵D是BC的中点
∴AD⊥BC
∵E是AC的中点
∴DE= AC=3
6.如图,△ABC中,∠C=90°,∠A=60 °,EF是AB的垂直平分线,判断CE与BE之间的关系
解:结论:CE= BE,连接AE
∵∠C=90°,∠A=60 °∴∠B=30°
∵EF是AB的垂直平分线,∴BE=AE
∴∠B=∠BAE=30°
∴∠BAE=30°
∴CE= AE
∴CE= BE
课堂小结
我们学习了直角三角形哪些性质?
性质1
直角三角形两个锐角互余
性质2
直角三角形的勾股定理
性质3
直角三角形斜边上的中线等于斜边的一半
性质4
直角三角形30 角所对直角边等于斜边的一半
