华师大版数学九年级上册24.3.1 第2课时 特殊角的三角函数值 同步课件(共16张PPT)
文档属性
| 名称 | 华师大版数学九年级上册24.3.1 第2课时 特殊角的三角函数值 同步课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 284.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 06:29:52 | ||
图片预览




文档简介
(共16张PPT)
24.3.1 第2课时 特殊角的三角函数值
第24章 解直角三角形
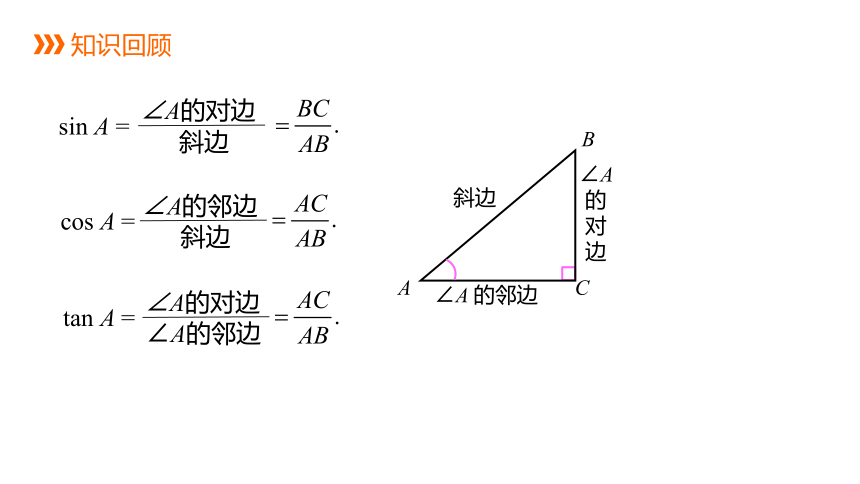
知识回顾
A
B
C
∠A 的邻边
∠A
的
对
边
斜边
∠A的对边
斜边
sin A =
∠A的邻边
斜边
cos A =
∠A的对边
∠A的邻边
tan A =
获取新知
如图,在Rt△ABC中,∠C=90°,∠A=30°,则
从而可得:
A
C
B
┐
30°
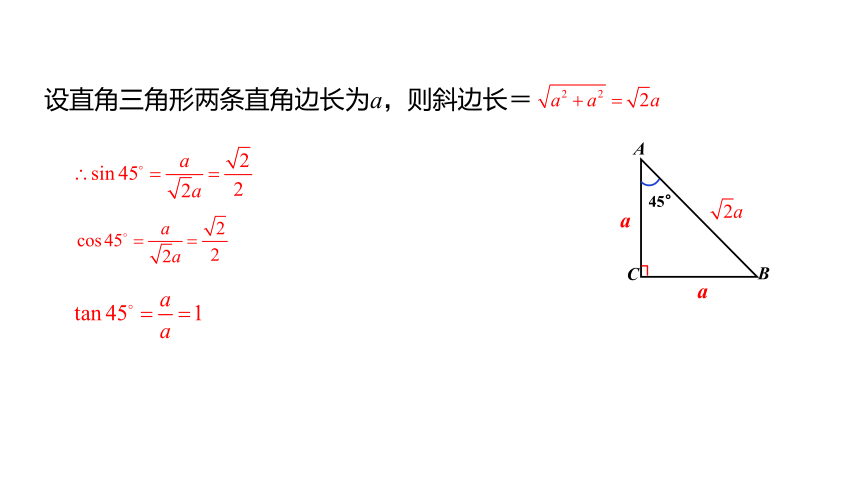
设直角三角形两条直角边长为a,则斜边长=
A
C
B
┐
45°
a
a
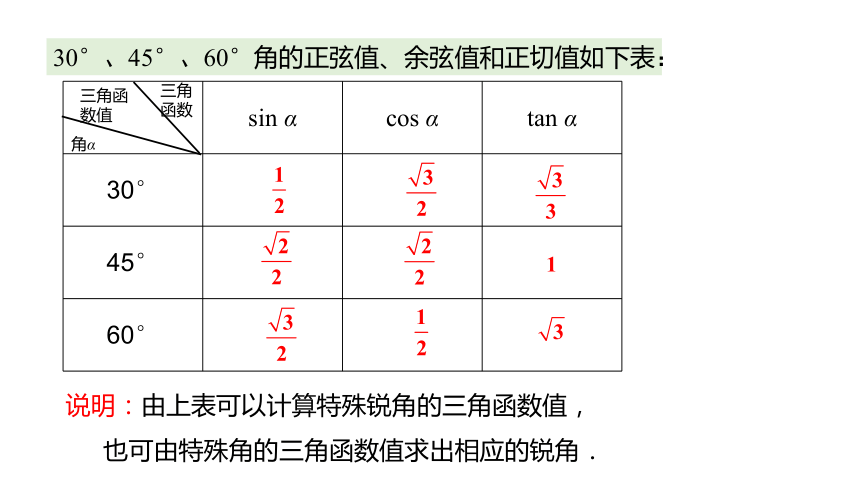
30°、45°、60°角的正弦值、余弦值和正切值如下表:
sin α cos α tan α
30°
45°
60°
三角函数
三角函数值
角α
说明:由上表可以计算特殊锐角的三角函数值,
也可由特殊角的三角函数值求出相应的锐角.
例题讲解
例1 求值:(1)sin 30° tan 30°+ cos60° tan60°.
(2)sin260°+cos260°-tan 45°
解: (1) sin 30° tan 30°+ cos60° tan60°
提示:sin260°表示(sin60°)2,
即(sin60°)×(sin60°).
例2 (1)如图(1),在Rt△ABC中,∠C=90°, AB= , BC= ,求∠A的度数.
A
B
C
解: (1)在图(1)中,
∴ ∠A = 45°.
(2)如图(2),AO是圆锥的高,OB是底面半径,
AO= OB,求 的度数.
(2)在图(2)中,
∴ α = 60°.
A
B
O
随堂演练
1. cos45°的值等于( )
B
2. 在△ABC中,若角A,B满足|cos A- |+(1-tan B)2=0,则∠C的大小是( )
A.45° B.60°
C.75° D.105°
D
3(1).如果∠α是等边三角形的一个内角,则cosα=____.
(2).在△ABC中,∠C=90°,若∠B=2∠A, tanA=____.
4.求下列各式的值:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
(3)
解:(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
课堂小结
巧记特殊锐角三角函数值的方法:
1. 三角板记忆法:借助如图所示的三角板记忆.
特点记忆法:30°,45°,60°角的正弦值记为
余弦值相反,正切值记为
3. 口诀记忆法:1,2,3;3,2,1;3,9,27;弦比2,切比3,分子根号别忘添.
24.3.1 第2课时 特殊角的三角函数值
第24章 解直角三角形
知识回顾
A
B
C
∠A 的邻边
∠A
的
对
边
斜边
∠A的对边
斜边
sin A =
∠A的邻边
斜边
cos A =
∠A的对边
∠A的邻边
tan A =
获取新知
如图,在Rt△ABC中,∠C=90°,∠A=30°,则
从而可得:
A
C
B
┐
30°
设直角三角形两条直角边长为a,则斜边长=
A
C
B
┐
45°
a
a
30°、45°、60°角的正弦值、余弦值和正切值如下表:
sin α cos α tan α
30°
45°
60°
三角函数
三角函数值
角α
说明:由上表可以计算特殊锐角的三角函数值,
也可由特殊角的三角函数值求出相应的锐角.
例题讲解
例1 求值:(1)sin 30° tan 30°+ cos60° tan60°.
(2)sin260°+cos260°-tan 45°
解: (1) sin 30° tan 30°+ cos60° tan60°
提示:sin260°表示(sin60°)2,
即(sin60°)×(sin60°).
例2 (1)如图(1),在Rt△ABC中,∠C=90°, AB= , BC= ,求∠A的度数.
A
B
C
解: (1)在图(1)中,
∴ ∠A = 45°.
(2)如图(2),AO是圆锥的高,OB是底面半径,
AO= OB,求 的度数.
(2)在图(2)中,
∴ α = 60°.
A
B
O
随堂演练
1. cos45°的值等于( )
B
2. 在△ABC中,若角A,B满足|cos A- |+(1-tan B)2=0,则∠C的大小是( )
A.45° B.60°
C.75° D.105°
D
3(1).如果∠α是等边三角形的一个内角,则cosα=____.
(2).在△ABC中,∠C=90°,若∠B=2∠A, tanA=____.
4.求下列各式的值:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
(3)
解:(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
课堂小结
巧记特殊锐角三角函数值的方法:
1. 三角板记忆法:借助如图所示的三角板记忆.
特点记忆法:30°,45°,60°角的正弦值记为
余弦值相反,正切值记为
3. 口诀记忆法:1,2,3;3,2,1;3,9,27;弦比2,切比3,分子根号别忘添.
