华师大版数学九年级上册24.3.1 第1课时 锐角三角函数的定义及关系应用 同步课件(共19张PPT)
文档属性
| 名称 | 华师大版数学九年级上册24.3.1 第1课时 锐角三角函数的定义及关系应用 同步课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 325.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
24.3.1 第1课时 锐角三角函数的定义及关系应用
第24章 解直角三角形
知识回顾
1.在Rt△ABC中,∠C=90°,AB=10,BC=6,AC=______.
8
2.在Rt△ABC中,∠C=90°,∠A=30°,AB=10cm,则BC= ,理由是 .
5
30°所对直角边是斜边的一半
情景导入
下面图1和图2中各有一个比较陡的梯子,你能把它们找出来吗?说说你的理由。
图1
图2
获取新知
在24.1节中,如图,我们曾经使用两种方法求出操场旗杆的高度,其中都出现了两个相似的直角三角形,即△ABC∽△A'B'C'
按1:500的比例,就一定有
就是它们的相似比
当然也有
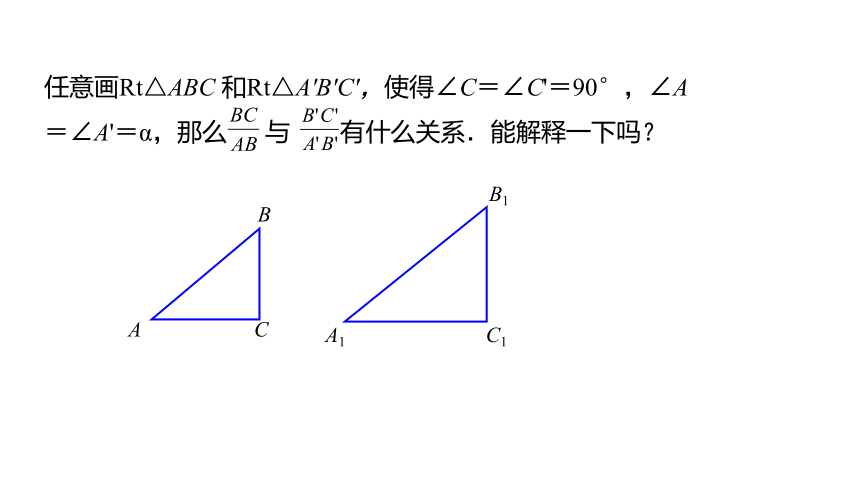
任意画Rt△ABC 和Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系.能解释一下吗?
A
B
C
A1
B1
C1
在图中,由于∠C=∠C'=90°,∠A=∠A'=α,所以Rt△ABC∽Rt△A'B'C'
这就是说,在直角三角形中,当锐角∠A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比也是一个固定值.
A
B
C
A1
B1
C1
A
C
B
┐
C1
C2
C3
B1
B2
B3
┐
┐
┐
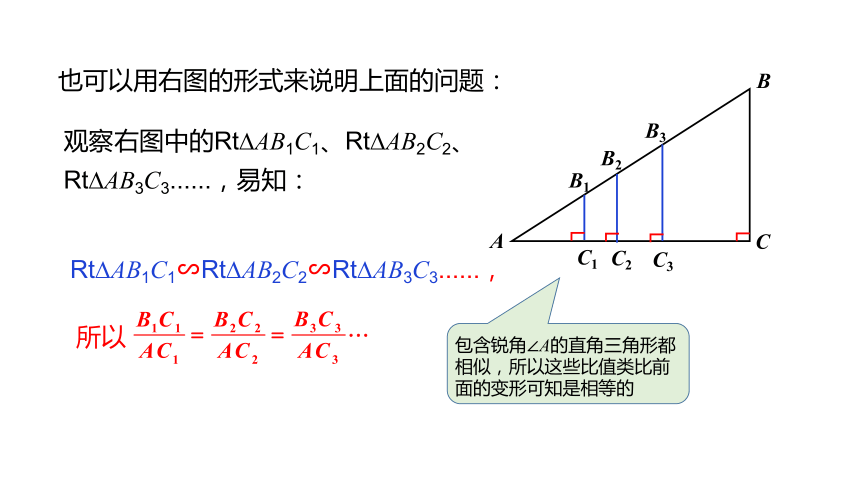
也可以用右图的形式来说明上面的问题:
观察右图中的Rt AB1C1、Rt AB2C2、Rt AB3C3......,易知:
Rt AB1C1∽Rt AB2C2∽Rt AB3C3......,
所以
包含锐角∠A的直角三角形都相似,所以这些比值类比前面的变形可知是相等的
在直角三角形中,当锐角∠A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比也是一个固定值.
同样,当锐角∠A的大小确定时,∠A的对边与邻边的比也是固定的;
同样,当锐角∠A的大小确定时,∠A的邻边与斜边的比也是固定的;
如图,在Rt△ABC中,∠C=90°,我们把锐角∠A的对边与斜边的比叫做∠A的正弦,记作sinA 即
A
B
C
c
a
b
对边
斜边
在图中
∠A的对边记作a
∠B的对边记作b
∠C的对边记作c
A
B
C
c
a
b
对边
斜边
在图中
∠A的对边记作a
∠B的对边记作b
∠C的对边记作c
如图,在Rt△ABC中,∠C=90°,我们把锐角∠A的邻边与斜边的比叫做∠A的余弦,记作cosA 即
把锐角∠A的对边与邻边的比叫做∠A的正切,
记作tanA 即
∠A的正弦、余弦、正切,统称为∠A的三角函数
邻边
正弦
余弦
A
B
C
c
a
b
对边
斜边
邻边
1.sinA、cosA是在直角三角形中定义的,∠A是锐角
(注意数形结合,构造直角三角形).
2.sinA、 cosA是一个比值(数值).
3.sinA、 cosA的大小只与∠A的大小有关,而与直角三角形的边长无关.
你知道这两个不等式成立的理由吗?你猜猜正切的取值范围
例题讲解
例 如图,在Rt△ABC中,∠C=90°, AC=15,BC=8.试求出∠A的三个三角函数值.
解:
A
B
C
┐
15
8
随堂演练
1.如图,在△ABC中,∠C=90°,AB=5,BC=3,则sinA的值是( )
A. B. C. D.
C
2.在△ABC中,若三边BC,CA,AB满足BC:CA:AB=5:12:13,则cos B的值是( )
A. B. C. D.
C
3. 在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tan B的值是( )
A. B. 3 C. D.
D
4.如图,∠α的顶点为O,它的一边在x轴的正半轴上,
另一边OA上有一点P(b,4),若sin α= ,则b=____.
3
5.下图中∠ACB=90°,CD⊥AB,垂足为D.完成下列填空.
A
B
C
D
(1) tanA =
=
AC
( )
CD
( )
(2) tanB=
=
BC
( )
CD
( )
BC
AD
BD
AC
6. 如图,在Rt△ABC中,∠C=90°,AC=8,tanA= ,求:sinA、cosB的值.
解:
A
B
C
8
课堂小结
在Rt△ABC中
A
B
C
c
a
b
对边
斜边
邻边
24.3.1 第1课时 锐角三角函数的定义及关系应用
第24章 解直角三角形
知识回顾
1.在Rt△ABC中,∠C=90°,AB=10,BC=6,AC=______.
8
2.在Rt△ABC中,∠C=90°,∠A=30°,AB=10cm,则BC= ,理由是 .
5
30°所对直角边是斜边的一半
情景导入
下面图1和图2中各有一个比较陡的梯子,你能把它们找出来吗?说说你的理由。
图1
图2
获取新知
在24.1节中,如图,我们曾经使用两种方法求出操场旗杆的高度,其中都出现了两个相似的直角三角形,即△ABC∽△A'B'C'
按1:500的比例,就一定有
就是它们的相似比
当然也有
任意画Rt△ABC 和Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系.能解释一下吗?
A
B
C
A1
B1
C1
在图中,由于∠C=∠C'=90°,∠A=∠A'=α,所以Rt△ABC∽Rt△A'B'C'
这就是说,在直角三角形中,当锐角∠A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比也是一个固定值.
A
B
C
A1
B1
C1
A
C
B
┐
C1
C2
C3
B1
B2
B3
┐
┐
┐
也可以用右图的形式来说明上面的问题:
观察右图中的Rt AB1C1、Rt AB2C2、Rt AB3C3......,易知:
Rt AB1C1∽Rt AB2C2∽Rt AB3C3......,
所以
包含锐角∠A的直角三角形都相似,所以这些比值类比前面的变形可知是相等的
在直角三角形中,当锐角∠A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比也是一个固定值.
同样,当锐角∠A的大小确定时,∠A的对边与邻边的比也是固定的;
同样,当锐角∠A的大小确定时,∠A的邻边与斜边的比也是固定的;
如图,在Rt△ABC中,∠C=90°,我们把锐角∠A的对边与斜边的比叫做∠A的正弦,记作sinA 即
A
B
C
c
a
b
对边
斜边
在图中
∠A的对边记作a
∠B的对边记作b
∠C的对边记作c
A
B
C
c
a
b
对边
斜边
在图中
∠A的对边记作a
∠B的对边记作b
∠C的对边记作c
如图,在Rt△ABC中,∠C=90°,我们把锐角∠A的邻边与斜边的比叫做∠A的余弦,记作cosA 即
把锐角∠A的对边与邻边的比叫做∠A的正切,
记作tanA 即
∠A的正弦、余弦、正切,统称为∠A的三角函数
邻边
正弦
余弦
A
B
C
c
a
b
对边
斜边
邻边
1.sinA、cosA是在直角三角形中定义的,∠A是锐角
(注意数形结合,构造直角三角形).
2.sinA、 cosA是一个比值(数值).
3.sinA、 cosA的大小只与∠A的大小有关,而与直角三角形的边长无关.
你知道这两个不等式成立的理由吗?你猜猜正切的取值范围
例题讲解
例 如图,在Rt△ABC中,∠C=90°, AC=15,BC=8.试求出∠A的三个三角函数值.
解:
A
B
C
┐
15
8
随堂演练
1.如图,在△ABC中,∠C=90°,AB=5,BC=3,则sinA的值是( )
A. B. C. D.
C
2.在△ABC中,若三边BC,CA,AB满足BC:CA:AB=5:12:13,则cos B的值是( )
A. B. C. D.
C
3. 在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tan B的值是( )
A. B. 3 C. D.
D
4.如图,∠α的顶点为O,它的一边在x轴的正半轴上,
另一边OA上有一点P(b,4),若sin α= ,则b=____.
3
5.下图中∠ACB=90°,CD⊥AB,垂足为D.完成下列填空.
A
B
C
D
(1) tanA =
=
AC
( )
CD
( )
(2) tanB=
=
BC
( )
CD
( )
BC
AD
BD
AC
6. 如图,在Rt△ABC中,∠C=90°,AC=8,tanA= ,求:sinA、cosB的值.
解:
A
B
C
8
课堂小结
在Rt△ABC中
A
B
C
c
a
b
对边
斜边
邻边
