华师大版数学九年级上册同步课件:24.4 解直角三角形(第1课时) (共16张PPT)
文档属性
| 名称 | 华师大版数学九年级上册同步课件:24.4 解直角三角形(第1课时) (共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 502.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 06:36:28 | ||
图片预览






文档简介
(共16张PPT)
24.4 第1课时 解直角三角形
第24章 解直角三角形
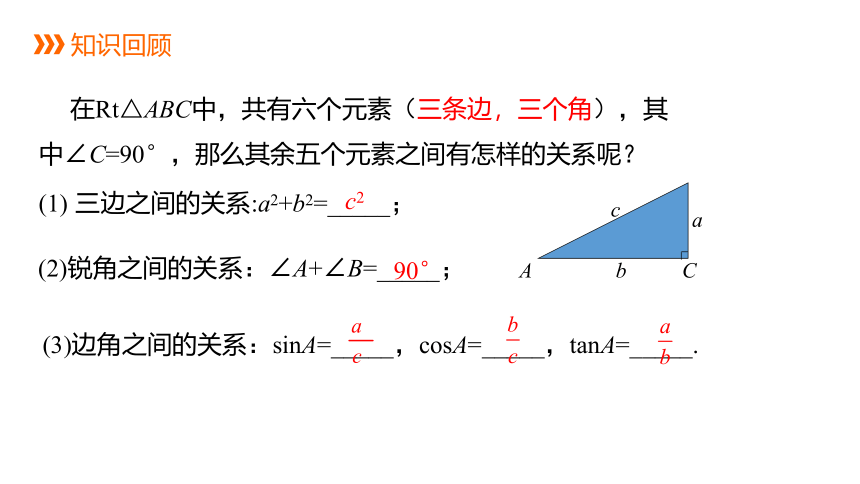
知识回顾
A
C
c
b
a
(1) 三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
例题讲解
例1 如图所示,一棵大树在一次强烈的地震中于离地面5米处折断倒下,树顶落在离树根12米处.大树在折断之前高多少?
解:利用勾股定理可以求出折断后剩下部分的长度为
答:大树在折断之前高为18米.
5m
12m
题型一:已知直角三角形两边解直角三角形
获取新知
事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
A
B
a
b
c
C
由直角三角形中已知的元素,求出所有未知元素的过程,叫做解直角三角形.
已知两直角边:
1.应用勾股定理求斜边;
2.应用角的正切值求出一锐角;
3.利用直角三角形的两锐角互余,求出另一锐角.
已知斜边和直角边:
1.利用勾股定理求出另一直角边;
2.再求一锐角的正弦或余弦值,即可求出一锐角;
3.利用直角三角形的两锐角互余,求出另一锐角.
例题讲解
题型二:已知一锐角一边解直角三角形
例2 如图,在相距2 000米的东、西两座炮台A、B处同时发现入侵敌舰C,在炮台A处测得敌舰 C 在它的南偏东40°的方向,在炮台B处测得敌舰C 在它的正南方.试求敌舰与两炮台的距离.(精确到1米)
┐
2000 m
40°
A
B
C
D
┐
2000 m
40°
A
B
C
D
解:在Rt△ABC中,
∵ ∠CAB=90°- ∠DAC=50°
∴
∵
∴
答:敌舰与A、B两炮台的距离分别约为3111米和2384米.
获取新知
已知直角三角形的一边和一锐角,解直角三角形时,若已知一直角边(邻边类似)a和一锐角A: ① ∠B=90 °- ∠ A;
②c=
若已知斜边c和一个锐角A: ① ∠ B=90°- ∠ A;
②a=c·sin A ; ③b=c·cos A.
随堂演练
1.在直角三角形ABC中,已知∠C=90°,
∠A=40°,BC=3,则AC的长等于( )
A.3sin 40° B.3sin 50°
C.3tan 40° D.3tan 50°
D
2.如图,△ABC中,∠C=90°,AC=3,∠B=30°,
P是BC边上的动点,则AP的长不可能是( )
A.3.5 B.4.2 C.5.8 D.7
D
3.在△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c.
(1)若已知a与∠B,则b= ,c= ;
(2)若已知∠A与c,则a= ,b= .
a tanB
c sinA
c cosA
4.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,a= ,c=2,则∠A= °,b= .
45
5.如图,在Rt△ABC中,∠C=90°, ,解这个直角三角形.
解:
A
B
C
6.如图,海面上B,C两岛分别位于A岛的正东和正北方向.一艘船从A岛出发,以18海里/时的速度向正北方向航行2小时到达C岛,此时测得B岛在C岛的南偏东43°方向上,求A,B两岛之间的距离.(结果精确到0.1海里.参考数:sin43°≈0.68,cos43°≈0.73,
tan43°≈0.93)
解:根据路程=速度×时间,可得AC=18×2=36(海里).
在Rt△ABC中,
利用正切函数的定义可得tan∠ACB= ,
由此可知AB=AC·tan∠ACB≈36×0.93≈33.5(海里).
答:A,B两岛之间的距离约为33.5海里.
课堂小结
1.数形结合思想.
方法:把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,构造出直角三角形.
2.方程思想.
3.转化(化归)思想.
解题思想与方法总结
24.4 第1课时 解直角三角形
第24章 解直角三角形
知识回顾
A
C
c
b
a
(1) 三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
例题讲解
例1 如图所示,一棵大树在一次强烈的地震中于离地面5米处折断倒下,树顶落在离树根12米处.大树在折断之前高多少?
解:利用勾股定理可以求出折断后剩下部分的长度为
答:大树在折断之前高为18米.
5m
12m
题型一:已知直角三角形两边解直角三角形
获取新知
事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
A
B
a
b
c
C
由直角三角形中已知的元素,求出所有未知元素的过程,叫做解直角三角形.
已知两直角边:
1.应用勾股定理求斜边;
2.应用角的正切值求出一锐角;
3.利用直角三角形的两锐角互余,求出另一锐角.
已知斜边和直角边:
1.利用勾股定理求出另一直角边;
2.再求一锐角的正弦或余弦值,即可求出一锐角;
3.利用直角三角形的两锐角互余,求出另一锐角.
例题讲解
题型二:已知一锐角一边解直角三角形
例2 如图,在相距2 000米的东、西两座炮台A、B处同时发现入侵敌舰C,在炮台A处测得敌舰 C 在它的南偏东40°的方向,在炮台B处测得敌舰C 在它的正南方.试求敌舰与两炮台的距离.(精确到1米)
┐
2000 m
40°
A
B
C
D
┐
2000 m
40°
A
B
C
D
解:在Rt△ABC中,
∵ ∠CAB=90°- ∠DAC=50°
∴
∵
∴
答:敌舰与A、B两炮台的距离分别约为3111米和2384米.
获取新知
已知直角三角形的一边和一锐角,解直角三角形时,若已知一直角边(邻边类似)a和一锐角A: ① ∠B=90 °- ∠ A;
②c=
若已知斜边c和一个锐角A: ① ∠ B=90°- ∠ A;
②a=c·sin A ; ③b=c·cos A.
随堂演练
1.在直角三角形ABC中,已知∠C=90°,
∠A=40°,BC=3,则AC的长等于( )
A.3sin 40° B.3sin 50°
C.3tan 40° D.3tan 50°
D
2.如图,△ABC中,∠C=90°,AC=3,∠B=30°,
P是BC边上的动点,则AP的长不可能是( )
A.3.5 B.4.2 C.5.8 D.7
D
3.在△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c.
(1)若已知a与∠B,则b= ,c= ;
(2)若已知∠A与c,则a= ,b= .
a tanB
c sinA
c cosA
4.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,a= ,c=2,则∠A= °,b= .
45
5.如图,在Rt△ABC中,∠C=90°, ,解这个直角三角形.
解:
A
B
C
6.如图,海面上B,C两岛分别位于A岛的正东和正北方向.一艘船从A岛出发,以18海里/时的速度向正北方向航行2小时到达C岛,此时测得B岛在C岛的南偏东43°方向上,求A,B两岛之间的距离.(结果精确到0.1海里.参考数:sin43°≈0.68,cos43°≈0.73,
tan43°≈0.93)
解:根据路程=速度×时间,可得AC=18×2=36(海里).
在Rt△ABC中,
利用正切函数的定义可得tan∠ACB= ,
由此可知AB=AC·tan∠ACB≈36×0.93≈33.5(海里).
答:A,B两岛之间的距离约为33.5海里.
课堂小结
1.数形结合思想.
方法:把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,构造出直角三角形.
2.方程思想.
3.转化(化归)思想.
解题思想与方法总结
