华师大版数学九年级上册同步课件:24.4 解直角三角形的应用 (第3课时) (共22张PPT)
文档属性
| 名称 | 华师大版数学九年级上册同步课件:24.4 解直角三角形的应用 (第3课时) (共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 368.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 06:38:58 | ||
图片预览








文档简介
(共22张PPT)
24.4 第3课时 解直角三角形的应用—俯角和仰角
第24章 解直角三角形
知识回顾
A
C
c
b
a
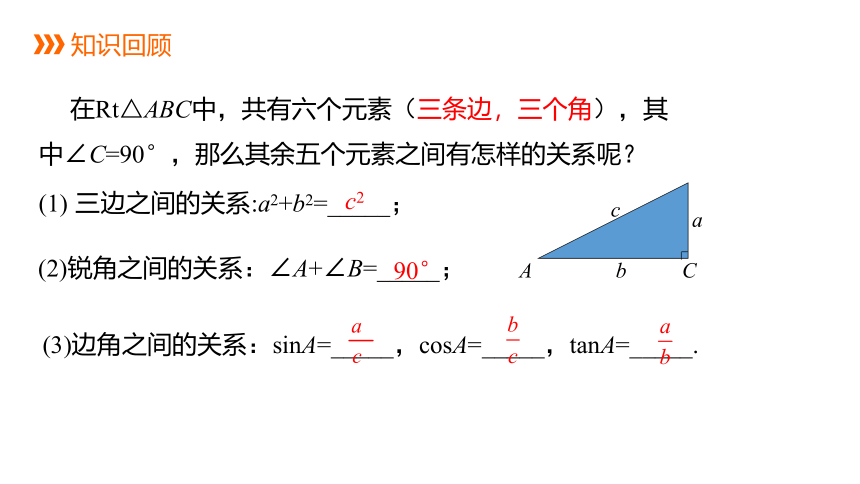
(1) 三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
获取新知
在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
铅直线
水平线
视线
视线
仰角
俯角
例题讲解
例 如图24.4.4,为了测量旗杆的高度BC,在离旗杆底部10米的A处,用高1. 50米的测角仪DA测得旗杆顶端C的仰角α= 52°.求旗杆BC的高.(精确到0. 1米)
解: 在 Rt△CDE中,
∵ CE = DE × tan α = AB × tan α
= 10× tan 52°
≈12.80,
∴BC = BE + CE=DA + CE
≈1. 50 + 12. 80
= 14.3(米).
答:旗杆BC的高度约为14. 3米.
随堂演练
1.如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
A. B.30sin α 米
C.30tan α 米 D.30cos α 米
C
2.湖南路大桥于今年5月1日竣工,为徒骇河景区增添上一道亮丽的风景线.某校数学兴趣小组用测量仪器测量该大桥的桥塔高度,在距桥塔AB底部50米的C处,测得桥塔顶部A的仰角为41.5° (如图).已知测量仪器CD的高度为1米,则桥塔AB的高度约为( )
(参考数据:sin 41.5°≈0.663,cos 41.5°≈0.749,
tan 41.5°≈0.885)
A.34米 B.38米
C.45米 D.50米
C
41.5°
A
B
C
D
50m
┐
3.如图1,在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC=_____米.
4.如图2,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为_____米.
100
图1
图2
5.建筑物BC上有一旗杆AB,由距BC有40m的D处观察旗杆顶部A的仰角54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).
解:在等腰三角形BCD中∠ACD=90°
BC=DC=40m
所以AB=AC-BC=55.2-40=15.2
答:旗杆的高度为15.2m.
在Rt△ACD中
A
B
C
D
40m
54°
45°
A
B
C
D
40m
54°
45°
课堂小结
解答含有仰角、俯角问题的方法
1.仰角和俯角是指视线相对于水平线而言的,不同位置的仰角和俯角是不同的;可巧记为“上仰下俯”.在测量物体的高度时,要善于将实际问题抽象为数学问题.
2. 视线、水平线、物体的高构成直角三角形,已知仰角(俯角)和另一边,利用解直角三角形的知识就可以求出物体的高度.
3.弄清仰角、俯角的定义,根据题意画出几何图形,将实际问题中的数量关系归结到直角三角形中来求解.
24.4 第4课时 解直角三角形的应用—坡度、坡角
第24章 解直角三角形
知识回顾
A
C
c
b
a
(1) 三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
获取新知
1. 坡角
坡面与水平面的夹角叫做坡角,记作 α .
2. 坡度 (或坡比)
坡度通常写成 1∶m的形式,如i=1∶6.
如图所示,坡面的铅垂高度 (h) 和水平长度 (l) 的比叫做坡面的坡度 (或坡比),记作i, 即 i = h : l .
α
l
h
i= h : l
坡面
水平面
3.坡度与坡角的关系
坡度等于坡角的正切值
坡度越大,坡角α就越大,坡面就越陡,
即tan α的值就越大.
α
l
h
i= h : l
坡面
水平面
例题讲解
例 如图,一段路基的横断面是梯形,高为4. 2米,上底宽为12. 51米,路基的坡面与地面的倾角分別是32°和28°,求路基下底的宽.(精确到0. 1米)
12.51米
4.2米
A
B
C
D
E
F
┐
┐
32°
28°
解: 作DE⊥AB,CF⊥AB,垂足分别为点E、F 由题意
可知 DE = CF = 4.2, EF = CD = 12.51.
在 Rt△ADE 中,
在Rt△ BCF中,同理可得
∴AB = AE + EF + BF
≈6. 72 + 12.51 +7.90≈27. 1(米).
答:路基下底的宽约为27. 1米.
12.51米
4.2米
A
B
C
D
E
F
┐
┐
32°
28°
随堂演练
1.堤的横断面如图.堤高BC是5米,迎水斜坡AB的长是13米,那么斜坡AB的坡度是( )
A.1∶3 B.1∶2.6 C.1∶2.4 D.1∶2
C
2.拦水坝横断面如图所示,迎水坡AB的坡比是1∶ ,坝高BC=10 m,则坡面AB的长度是( )
A.15 m B.20 m C.10 m D.20 m
D
3. 如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=2 000米,则他实际上升了______米.
1000
4(1).斜坡的坡度是 ,则坡角α=___度.
(2).斜坡的坡角是45°,则坡比是 _____.
(3).斜坡长是12米,坡高6米,则坡比是_______.
30
1:1
5. 如图所示,小山岗的斜坡AC的坡度tan α= ,在与山脚C距离200 m的D处,测得山顶A的仰角为26.6°,求小山岗的高AB.(结果取整数,参考数据:sin 26.6°≈ 0.45,cos 26.6°≈ 0.89,tan 26.6°≈ 0.50)
解: 设小山岗的高AB为x m,在Rt△ABC中,
∴BC= x m.
∴BD=DC+BC=
∵在Rt△ABD中,tan∠ADB=
tan 26.6°≈0.50,
∴ ≈0.50,解得x≈300.
答:小山岗的高AB约为300 m.
课堂小结
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题,也就是建立适当的数学模型);
(2)根据条件的特点,适当选用锐角三角函数,运用直
角三角形的有关性质,解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
24.4 第3课时 解直角三角形的应用—俯角和仰角
第24章 解直角三角形
知识回顾
A
C
c
b
a
(1) 三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
获取新知
在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
铅直线
水平线
视线
视线
仰角
俯角
例题讲解
例 如图24.4.4,为了测量旗杆的高度BC,在离旗杆底部10米的A处,用高1. 50米的测角仪DA测得旗杆顶端C的仰角α= 52°.求旗杆BC的高.(精确到0. 1米)
解: 在 Rt△CDE中,
∵ CE = DE × tan α = AB × tan α
= 10× tan 52°
≈12.80,
∴BC = BE + CE=DA + CE
≈1. 50 + 12. 80
= 14.3(米).
答:旗杆BC的高度约为14. 3米.
随堂演练
1.如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
A. B.30sin α 米
C.30tan α 米 D.30cos α 米
C
2.湖南路大桥于今年5月1日竣工,为徒骇河景区增添上一道亮丽的风景线.某校数学兴趣小组用测量仪器测量该大桥的桥塔高度,在距桥塔AB底部50米的C处,测得桥塔顶部A的仰角为41.5° (如图).已知测量仪器CD的高度为1米,则桥塔AB的高度约为( )
(参考数据:sin 41.5°≈0.663,cos 41.5°≈0.749,
tan 41.5°≈0.885)
A.34米 B.38米
C.45米 D.50米
C
41.5°
A
B
C
D
50m
┐
3.如图1,在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC=_____米.
4.如图2,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为_____米.
100
图1
图2
5.建筑物BC上有一旗杆AB,由距BC有40m的D处观察旗杆顶部A的仰角54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).
解:在等腰三角形BCD中∠ACD=90°
BC=DC=40m
所以AB=AC-BC=55.2-40=15.2
答:旗杆的高度为15.2m.
在Rt△ACD中
A
B
C
D
40m
54°
45°
A
B
C
D
40m
54°
45°
课堂小结
解答含有仰角、俯角问题的方法
1.仰角和俯角是指视线相对于水平线而言的,不同位置的仰角和俯角是不同的;可巧记为“上仰下俯”.在测量物体的高度时,要善于将实际问题抽象为数学问题.
2. 视线、水平线、物体的高构成直角三角形,已知仰角(俯角)和另一边,利用解直角三角形的知识就可以求出物体的高度.
3.弄清仰角、俯角的定义,根据题意画出几何图形,将实际问题中的数量关系归结到直角三角形中来求解.
24.4 第4课时 解直角三角形的应用—坡度、坡角
第24章 解直角三角形
知识回顾
A
C
c
b
a
(1) 三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
获取新知
1. 坡角
坡面与水平面的夹角叫做坡角,记作 α .
2. 坡度 (或坡比)
坡度通常写成 1∶m的形式,如i=1∶6.
如图所示,坡面的铅垂高度 (h) 和水平长度 (l) 的比叫做坡面的坡度 (或坡比),记作i, 即 i = h : l .
α
l
h
i= h : l
坡面
水平面
3.坡度与坡角的关系
坡度等于坡角的正切值
坡度越大,坡角α就越大,坡面就越陡,
即tan α的值就越大.
α
l
h
i= h : l
坡面
水平面
例题讲解
例 如图,一段路基的横断面是梯形,高为4. 2米,上底宽为12. 51米,路基的坡面与地面的倾角分別是32°和28°,求路基下底的宽.(精确到0. 1米)
12.51米
4.2米
A
B
C
D
E
F
┐
┐
32°
28°
解: 作DE⊥AB,CF⊥AB,垂足分别为点E、F 由题意
可知 DE = CF = 4.2, EF = CD = 12.51.
在 Rt△ADE 中,
在Rt△ BCF中,同理可得
∴AB = AE + EF + BF
≈6. 72 + 12.51 +7.90≈27. 1(米).
答:路基下底的宽约为27. 1米.
12.51米
4.2米
A
B
C
D
E
F
┐
┐
32°
28°
随堂演练
1.堤的横断面如图.堤高BC是5米,迎水斜坡AB的长是13米,那么斜坡AB的坡度是( )
A.1∶3 B.1∶2.6 C.1∶2.4 D.1∶2
C
2.拦水坝横断面如图所示,迎水坡AB的坡比是1∶ ,坝高BC=10 m,则坡面AB的长度是( )
A.15 m B.20 m C.10 m D.20 m
D
3. 如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=2 000米,则他实际上升了______米.
1000
4(1).斜坡的坡度是 ,则坡角α=___度.
(2).斜坡的坡角是45°,则坡比是 _____.
(3).斜坡长是12米,坡高6米,则坡比是_______.
30
1:1
5. 如图所示,小山岗的斜坡AC的坡度tan α= ,在与山脚C距离200 m的D处,测得山顶A的仰角为26.6°,求小山岗的高AB.(结果取整数,参考数据:sin 26.6°≈ 0.45,cos 26.6°≈ 0.89,tan 26.6°≈ 0.50)
解: 设小山岗的高AB为x m,在Rt△ABC中,
∴BC= x m.
∴BD=DC+BC=
∵在Rt△ABD中,tan∠ADB=
tan 26.6°≈0.50,
∴ ≈0.50,解得x≈300.
答:小山岗的高AB约为300 m.
课堂小结
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题,也就是建立适当的数学模型);
(2)根据条件的特点,适当选用锐角三角函数,运用直
角三角形的有关性质,解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
