物理人教版(2019)必修第二册 6.2 向心力 6.3向心加速度(共27张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册 6.2 向心力 6.3向心加速度(共27张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-25 15:47:52 | ||
图片预览






文档简介
(共27张PPT)
第六章 圆周运动
第二节 向心力
第三节 向心加速度
1
2
复习:圆周运动
圆周运动:速度方向时刻改变
速度改变:加速度不为零
合外力不为零
加速度与合外力有什么关系?
匀速圆周运动的加速度与合外力有什么特点?
圆周运动速度方向:沿切线指向前进方向
3
匀速圆周运动的速度与速度变化量
匀速圆周运动速度变化量方向:指向圆心
匀速圆周运动速度变化量大小:
加速度方向如何?
向心加速度:做匀速圆周运动的物体的加速度总指向圆心,因此把它叫作向心加速度。向心加速度用表示。
思考:做匀速圆周运动的物体所受合外力与加速度有什么关系?
牛顿第二定律:F=ma;牛顿第二定律适用条件:宏观低速。
向心力:做匀速圆周运动的物体所受的合力总指向圆心,这个指向圆心的力就叫作向心力。向心力用表示。
4
向心加速度与向心力
注意:向心力是效果力,不是性质力(我们所学过的重力、支持力、摩擦力等,都是性质力)。因此不能说“某物体受到向心力的作用”。
向心力:做匀速圆周运动的物体受到的指向圆心的合力。
向心力的方向:始终指向圆心/与速度方向垂直(不断变化)
向心力的作用:只改变线速度的方向,而不改变其大小
向心力是根据力的作用效果命名的,它是匀速圆周运动的物体所受的合力,向心力可以由重力、弹力、摩擦力或由几个力的合力提供。
5
向心力的来源
向心力不是物体真实受到的一个力,不能说物体受到向心力的作用 ,只能说某个力或某几个力提供了向心力。
与速度共线的力改变速度的大小;与速度垂直的力改变速度的方向
6
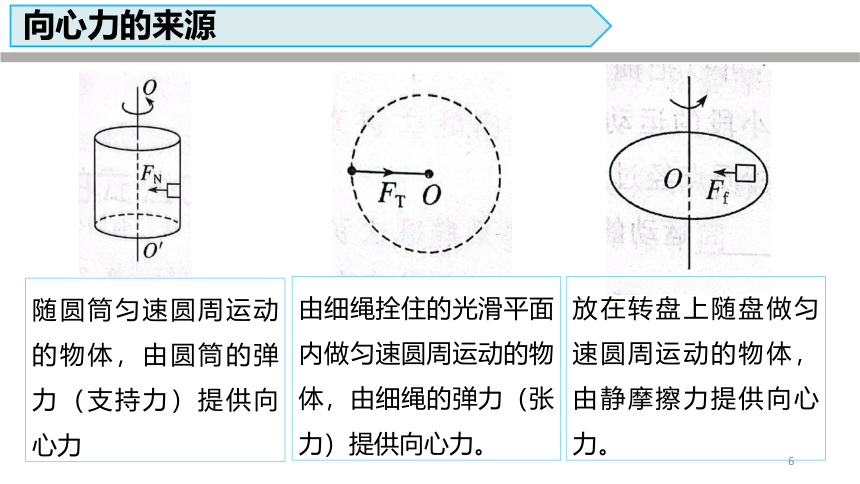
向心力的来源
随圆筒匀速圆周运动的物体,由圆筒的弹力(支持力)提供向心力
由细绳拴住的光滑平面内做匀速圆周运动的物体,由细绳的弹力(张力)提供向心力。
放在转盘上随盘做匀速圆周运动的物体,由静摩擦力提供向心力。
7
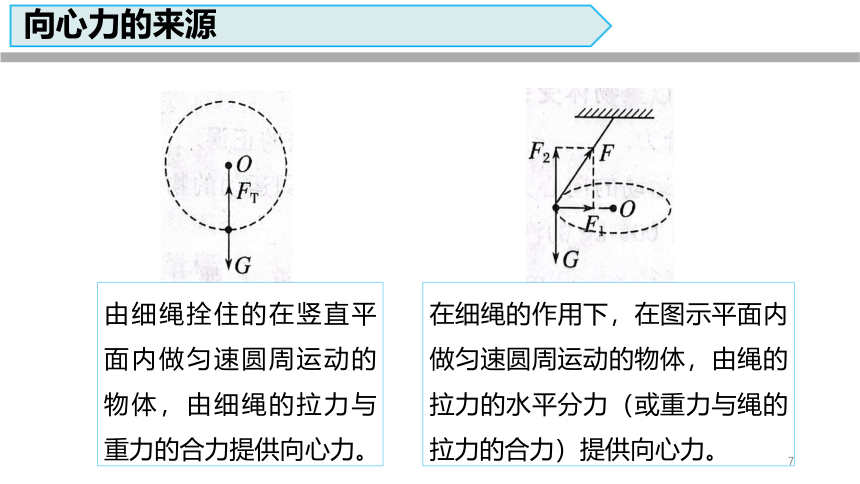
向心力的来源
由细绳拴住的在竖直平面内做匀速圆周运动的物体,由细绳的拉力与重力的合力提供向心力。
在细绳的作用下,在图示平面内做匀速圆周运动的物体,由绳的拉力的水平分力(或重力与绳的拉力的合力)提供向心力。
8
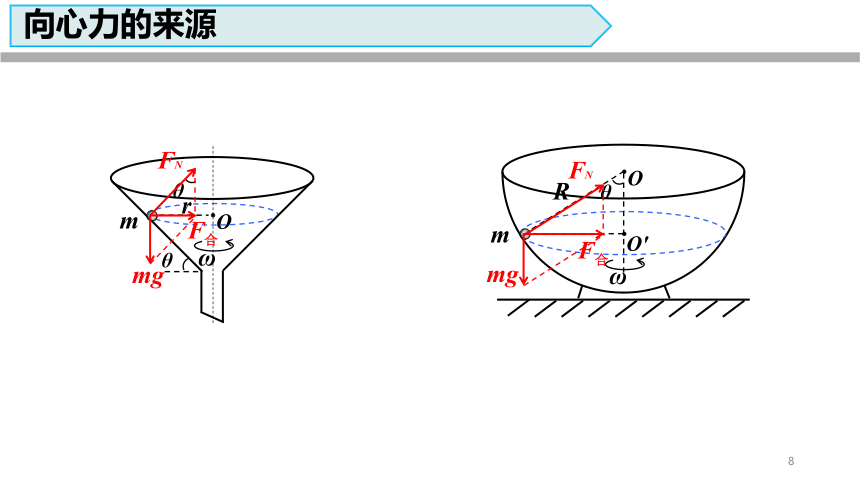
向心力的来源
θ
ω
θ
m
O
r
mg
FN
F合
O'
O
R
θ
ω
m
mg
FN
F合
9
关于向心力的说法正确的是( )
物体由于做圆周运动而产生了向心力
向心力不改变圆周运动中物体的线速度大小
对做匀速圆周运动的物体进行受力分析时,一定不要漏掉向心力
做匀速圆周运动的物体其向心力是不变的
10
O
一个质量为0.1kg的小球,用一根长为0.45m的细绳拴着,绳的另一端系在O点,让小球从图示位置从静止开始释放,运动到最低点时小球的速度为3m/s。(小球视为质点,绳不可伸长,取g=10m/s2)
(1)小球在释放时加速度是多少?
(2)分析小球运动到最低点时向心力的来源,画出小球受力示意图;
(3)小球到达最低点时绳对小球的拉力的大小。
11
如图所示,将一质量为m的摆球用长为L的细绳吊起,上端固定,使摆球在水平面内做匀速圆周运动,细绳就会沿圆锥面旋转,这样就构成一个圆锥摆,则关于摆球A的受力情况,下列说法中正确的是( )
A.摆球受重力、拉力和向心力的作用
B.摆球受拉力和向心力的作用
C.摆球受重力和拉力的作用
D.摆球受重力和向心力的作用
#
13
如图所示,物块P置于水平转盘上随转盘一起运动,图中c方向沿半径指向圆心,a方向与c方向垂直。当转盘逆时针转动时,下列说法正确的是
A.当转盘匀速转动时,P所受摩擦力方向为c
B.当转盘匀速转动时,P不受转盘的摩擦力
C.当转盘加速转动时,P所受摩擦力方向可能为a
D.当转盘减速转动时,P所受摩擦力方向可能为b
14
实验:探究向心力大小的表达式
手柄
塔轮
长槽
短槽
横臂
套筒
标尺
15
实验数据
实验条件
实验现象(预计)
实验结论
ma=2mb
ω r 一定
m ω 一定
ra=2rb
m r 一定
2ωa=ωb
实验方法:控制变量法,验证
16
实验过程与结果
实验数据与预计一致;
实验数据表明:做匀速圆周运动的物体的向心力与质量成正比,与角速度的平方成正比,与半径成正比。
;方向:指向圆心
17
如图所示的向心力演示器探究钢球做圆周运动所需向心力大小影响因素中,当两钢球质量、运动半径均相同,标尺上露出的格数比为1:9时,不计钢球与槽的摩擦,则( )
A.钢球受重力、竖直向上的支持力和水平方向的弹力
B.钢球受重力、竖直向上的支持力、水平方向的弹力和向心力
C.与皮带连接的两个变速塔轮的半径之比为3:1
D.与皮带连接的两个变速塔轮的半径之比为1:3
18
如图,半径为r的圆筒绕竖直中心轴转动,小橡皮块紧贴在圆筒内壁上,它与圆筒的动摩擦因数为μ,最大静摩擦力等于滑动摩擦力,要使小橡皮不落下,则圆筒的角速度至少为多大?
19
(课本P30)如图所示,一个圆盘在水平面内匀速转动,角速度是4rad/s。圆盘上距圆盘中心0.10m的位置有一个质量为0.10kg的小物体在随圆盘一起做匀速圆周运动。
(1)求小物体所受向心力的大小。
(2)关于小物体所受的向心力,甲、乙两人有不同意见:甲认为该向心力等于圆盘对小物体的静摩擦力,指向圆心;乙认为小物体有向前运动的趋势,静摩擦力方向和相对运动趋势方向相反,即向后,而不是和运动方向垂直,因此向心力不可能由静摩擦力提供。你的意见是什么?说明理由。
20
如图一个内壁光滑的圆锥形筒的轴线垂直水平面,圆锥筒固定,有质量相等的小球A和B沿着筒的内壁在水平面内做匀速圆周运动,则( )
A. 球A的角速度等于球B的角速度
B. 球A的线速度大于球B的线速度
C. 球A的运动周期小于球B的运动周期
D. 球A与球B对筒壁的压力相等
21
如图,金属块Q放在带光滑小孔的水平桌面上,一根穿过小孔的细线,上端固定在Q上,下端拴一个小球。小球在某一水平面内做匀速圆周运动(圆锥摆),细线与竖直方向成30°角(图中P位置)。现使小球在更高的水平面上做匀速圆周运动,细线与竖直方高成60°角(图中P'位置)。两种情况下,金属块Q都静止在桌面上的同一点,则后一种情况与原来相比较,下面判断正确的是( )
A. Q受到桌面的静摩擦力大小不变
B. 小球运动的角速度变大
C. 细线所受的拉力之比为2:1
D. 小球向心力大小之比为3:1
22
如图,半径为0.5m的半球形陶罐随水平转台一起绕过球心的竖直轴水平旋转,当旋转角速度为某一值ω0时,一质量为m的小物块恰好能无摩擦力地随陶罐一起与陶罐保持相对静止做匀速圆周运动,已知小物块与陶罐的球心O的连线跟竖直方向的夹角θ为37°,(g取10m/s2,sin37°取0.6,cos37°取0.8),则这个角速度ω0为( )
A.1rad/s
B.5rad/s
C.10rad/s
D.12rad/s
匀速圆周运动:向心力改变线速度的方向;合外力全部提供向心力
非匀速圆周运动:合外力不指向圆心;合外力的径向分量()作为向心力改变线速度的方向;切向分量与速度共线(与向心力垂直),改变线速度的大小
23
变速圆周运动和一般曲线运动
化繁为简:把一般曲线分割为许多很短的小段,每一段都可以看作圆周的一部分。这样,在分析质点经过曲线上某位置的运动时,就可以采用圆周运动的分析方法进行处理。
概念了解:曲率圆、曲率中心、曲率半径、曲率
24
一般的曲线运动
r1
r2
25
如图所示,长为L的细绳一端固定于O点,另一端系一个小球,在O点的正下方钉一个光滑的小钉子A,小球从一定高度摆下,当细绳与钉子相碰时,钉子的位置距小球L/4,则细绳碰到钉子前、后瞬间( )
A.绳对小球的拉力大小之比为1∶4
B.小球所受合外力大小之比为1∶4
C.小球做圆周运动的线速度大小之比为1∶4
D.小球做圆周运动的角速度之比为4∶1
26
一质点以匀速率在水平面上做曲线运动,其轨迹如图所示。从图中可以看出,质点在a,b、c,d四点处所受向心力最大的点(曲线较短时,近似看作圆周运动)( )
A.a
B.b
C.b
D.d
向心加速度:
向心力:
向心力与线速度垂直,向心力产生的向心加速度只改变线速度的方向;与线速度共线的力产生切向加速度,改变线速度的大小。
做匀速圆周运动的物体,合外力就是向心力;变速圆周运动的物体,其合外力的向心分力提供向心力。
27
总结
第六章 圆周运动
第二节 向心力
第三节 向心加速度
1
2
复习:圆周运动
圆周运动:速度方向时刻改变
速度改变:加速度不为零
合外力不为零
加速度与合外力有什么关系?
匀速圆周运动的加速度与合外力有什么特点?
圆周运动速度方向:沿切线指向前进方向
3
匀速圆周运动的速度与速度变化量
匀速圆周运动速度变化量方向:指向圆心
匀速圆周运动速度变化量大小:
加速度方向如何?
向心加速度:做匀速圆周运动的物体的加速度总指向圆心,因此把它叫作向心加速度。向心加速度用表示。
思考:做匀速圆周运动的物体所受合外力与加速度有什么关系?
牛顿第二定律:F=ma;牛顿第二定律适用条件:宏观低速。
向心力:做匀速圆周运动的物体所受的合力总指向圆心,这个指向圆心的力就叫作向心力。向心力用表示。
4
向心加速度与向心力
注意:向心力是效果力,不是性质力(我们所学过的重力、支持力、摩擦力等,都是性质力)。因此不能说“某物体受到向心力的作用”。
向心力:做匀速圆周运动的物体受到的指向圆心的合力。
向心力的方向:始终指向圆心/与速度方向垂直(不断变化)
向心力的作用:只改变线速度的方向,而不改变其大小
向心力是根据力的作用效果命名的,它是匀速圆周运动的物体所受的合力,向心力可以由重力、弹力、摩擦力或由几个力的合力提供。
5
向心力的来源
向心力不是物体真实受到的一个力,不能说物体受到向心力的作用 ,只能说某个力或某几个力提供了向心力。
与速度共线的力改变速度的大小;与速度垂直的力改变速度的方向
6
向心力的来源
随圆筒匀速圆周运动的物体,由圆筒的弹力(支持力)提供向心力
由细绳拴住的光滑平面内做匀速圆周运动的物体,由细绳的弹力(张力)提供向心力。
放在转盘上随盘做匀速圆周运动的物体,由静摩擦力提供向心力。
7
向心力的来源
由细绳拴住的在竖直平面内做匀速圆周运动的物体,由细绳的拉力与重力的合力提供向心力。
在细绳的作用下,在图示平面内做匀速圆周运动的物体,由绳的拉力的水平分力(或重力与绳的拉力的合力)提供向心力。
8
向心力的来源
θ
ω
θ
m
O
r
mg
FN
F合
O'
O
R
θ
ω
m
mg
FN
F合
9
关于向心力的说法正确的是( )
物体由于做圆周运动而产生了向心力
向心力不改变圆周运动中物体的线速度大小
对做匀速圆周运动的物体进行受力分析时,一定不要漏掉向心力
做匀速圆周运动的物体其向心力是不变的
10
O
一个质量为0.1kg的小球,用一根长为0.45m的细绳拴着,绳的另一端系在O点,让小球从图示位置从静止开始释放,运动到最低点时小球的速度为3m/s。(小球视为质点,绳不可伸长,取g=10m/s2)
(1)小球在释放时加速度是多少?
(2)分析小球运动到最低点时向心力的来源,画出小球受力示意图;
(3)小球到达最低点时绳对小球的拉力的大小。
11
如图所示,将一质量为m的摆球用长为L的细绳吊起,上端固定,使摆球在水平面内做匀速圆周运动,细绳就会沿圆锥面旋转,这样就构成一个圆锥摆,则关于摆球A的受力情况,下列说法中正确的是( )
A.摆球受重力、拉力和向心力的作用
B.摆球受拉力和向心力的作用
C.摆球受重力和拉力的作用
D.摆球受重力和向心力的作用
#
13
如图所示,物块P置于水平转盘上随转盘一起运动,图中c方向沿半径指向圆心,a方向与c方向垂直。当转盘逆时针转动时,下列说法正确的是
A.当转盘匀速转动时,P所受摩擦力方向为c
B.当转盘匀速转动时,P不受转盘的摩擦力
C.当转盘加速转动时,P所受摩擦力方向可能为a
D.当转盘减速转动时,P所受摩擦力方向可能为b
14
实验:探究向心力大小的表达式
手柄
塔轮
长槽
短槽
横臂
套筒
标尺
15
实验数据
实验条件
实验现象(预计)
实验结论
ma=2mb
ω r 一定
m ω 一定
ra=2rb
m r 一定
2ωa=ωb
实验方法:控制变量法,验证
16
实验过程与结果
实验数据与预计一致;
实验数据表明:做匀速圆周运动的物体的向心力与质量成正比,与角速度的平方成正比,与半径成正比。
;方向:指向圆心
17
如图所示的向心力演示器探究钢球做圆周运动所需向心力大小影响因素中,当两钢球质量、运动半径均相同,标尺上露出的格数比为1:9时,不计钢球与槽的摩擦,则( )
A.钢球受重力、竖直向上的支持力和水平方向的弹力
B.钢球受重力、竖直向上的支持力、水平方向的弹力和向心力
C.与皮带连接的两个变速塔轮的半径之比为3:1
D.与皮带连接的两个变速塔轮的半径之比为1:3
18
如图,半径为r的圆筒绕竖直中心轴转动,小橡皮块紧贴在圆筒内壁上,它与圆筒的动摩擦因数为μ,最大静摩擦力等于滑动摩擦力,要使小橡皮不落下,则圆筒的角速度至少为多大?
19
(课本P30)如图所示,一个圆盘在水平面内匀速转动,角速度是4rad/s。圆盘上距圆盘中心0.10m的位置有一个质量为0.10kg的小物体在随圆盘一起做匀速圆周运动。
(1)求小物体所受向心力的大小。
(2)关于小物体所受的向心力,甲、乙两人有不同意见:甲认为该向心力等于圆盘对小物体的静摩擦力,指向圆心;乙认为小物体有向前运动的趋势,静摩擦力方向和相对运动趋势方向相反,即向后,而不是和运动方向垂直,因此向心力不可能由静摩擦力提供。你的意见是什么?说明理由。
20
如图一个内壁光滑的圆锥形筒的轴线垂直水平面,圆锥筒固定,有质量相等的小球A和B沿着筒的内壁在水平面内做匀速圆周运动,则( )
A. 球A的角速度等于球B的角速度
B. 球A的线速度大于球B的线速度
C. 球A的运动周期小于球B的运动周期
D. 球A与球B对筒壁的压力相等
21
如图,金属块Q放在带光滑小孔的水平桌面上,一根穿过小孔的细线,上端固定在Q上,下端拴一个小球。小球在某一水平面内做匀速圆周运动(圆锥摆),细线与竖直方向成30°角(图中P位置)。现使小球在更高的水平面上做匀速圆周运动,细线与竖直方高成60°角(图中P'位置)。两种情况下,金属块Q都静止在桌面上的同一点,则后一种情况与原来相比较,下面判断正确的是( )
A. Q受到桌面的静摩擦力大小不变
B. 小球运动的角速度变大
C. 细线所受的拉力之比为2:1
D. 小球向心力大小之比为3:1
22
如图,半径为0.5m的半球形陶罐随水平转台一起绕过球心的竖直轴水平旋转,当旋转角速度为某一值ω0时,一质量为m的小物块恰好能无摩擦力地随陶罐一起与陶罐保持相对静止做匀速圆周运动,已知小物块与陶罐的球心O的连线跟竖直方向的夹角θ为37°,(g取10m/s2,sin37°取0.6,cos37°取0.8),则这个角速度ω0为( )
A.1rad/s
B.5rad/s
C.10rad/s
D.12rad/s
匀速圆周运动:向心力改变线速度的方向;合外力全部提供向心力
非匀速圆周运动:合外力不指向圆心;合外力的径向分量()作为向心力改变线速度的方向;切向分量与速度共线(与向心力垂直),改变线速度的大小
23
变速圆周运动和一般曲线运动
化繁为简:把一般曲线分割为许多很短的小段,每一段都可以看作圆周的一部分。这样,在分析质点经过曲线上某位置的运动时,就可以采用圆周运动的分析方法进行处理。
概念了解:曲率圆、曲率中心、曲率半径、曲率
24
一般的曲线运动
r1
r2
25
如图所示,长为L的细绳一端固定于O点,另一端系一个小球,在O点的正下方钉一个光滑的小钉子A,小球从一定高度摆下,当细绳与钉子相碰时,钉子的位置距小球L/4,则细绳碰到钉子前、后瞬间( )
A.绳对小球的拉力大小之比为1∶4
B.小球所受合外力大小之比为1∶4
C.小球做圆周运动的线速度大小之比为1∶4
D.小球做圆周运动的角速度之比为4∶1
26
一质点以匀速率在水平面上做曲线运动,其轨迹如图所示。从图中可以看出,质点在a,b、c,d四点处所受向心力最大的点(曲线较短时,近似看作圆周运动)( )
A.a
B.b
C.b
D.d
向心加速度:
向心力:
向心力与线速度垂直,向心力产生的向心加速度只改变线速度的方向;与线速度共线的力产生切向加速度,改变线速度的大小。
做匀速圆周运动的物体,合外力就是向心力;变速圆周运动的物体,其合外力的向心分力提供向心力。
27
总结
