沪科版数学八年级下册 18.2 勾股定理的逆定理-教案
文档属性
| 名称 | 沪科版数学八年级下册 18.2 勾股定理的逆定理-教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 60.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-25 00:00:00 | ||
图片预览

文档简介
两点之间的距离
版本 沪科版 授课教师
教 学 目 标 知识与技能: 掌握两点间的距离公式及其运用,以及会用坐标公式求出相应的解。 过程与方法: 通过独立思考和小组交流的方式,学生的独立思考和交流合作的能力得到提高。 情感、态度与价值观: 通过一系列的活动探究过程,体验数学活动充满着探索性和创造性,增强学习数学的学习兴趣。
教学重点 两点间的距离公式及其运用,掌握中点坐标的公式
教学难点 两点间的距离公式和中点坐标公式的推导
教学准备 多媒体、导学案
教学过程
环节设计 教学内容 教师活动 学生活动 设计意图
复 习 引 入 1、前面咱们刚刚学习了勾股定理及其逆定理,同学们还能复述这两个定理吗? 2、在前面学习的基础上,今天我们一起来探究平面内两点之间的距离。 复习引入 互动交流 积极回顾 认真回答 通过复习回顾,创设问题情境,调动学生学习兴趣和积极性。
新 知 探 究 活动一: (
B
) (
O
) (
A
) 如果数轴上的点A,B分别表示数 , ,A,B两点间的距离如何表示? 多媒体展示 思考 回答 为新课学习铺垫
新 知 探 究 活动二: (
O
y
x
) (
O
y
x
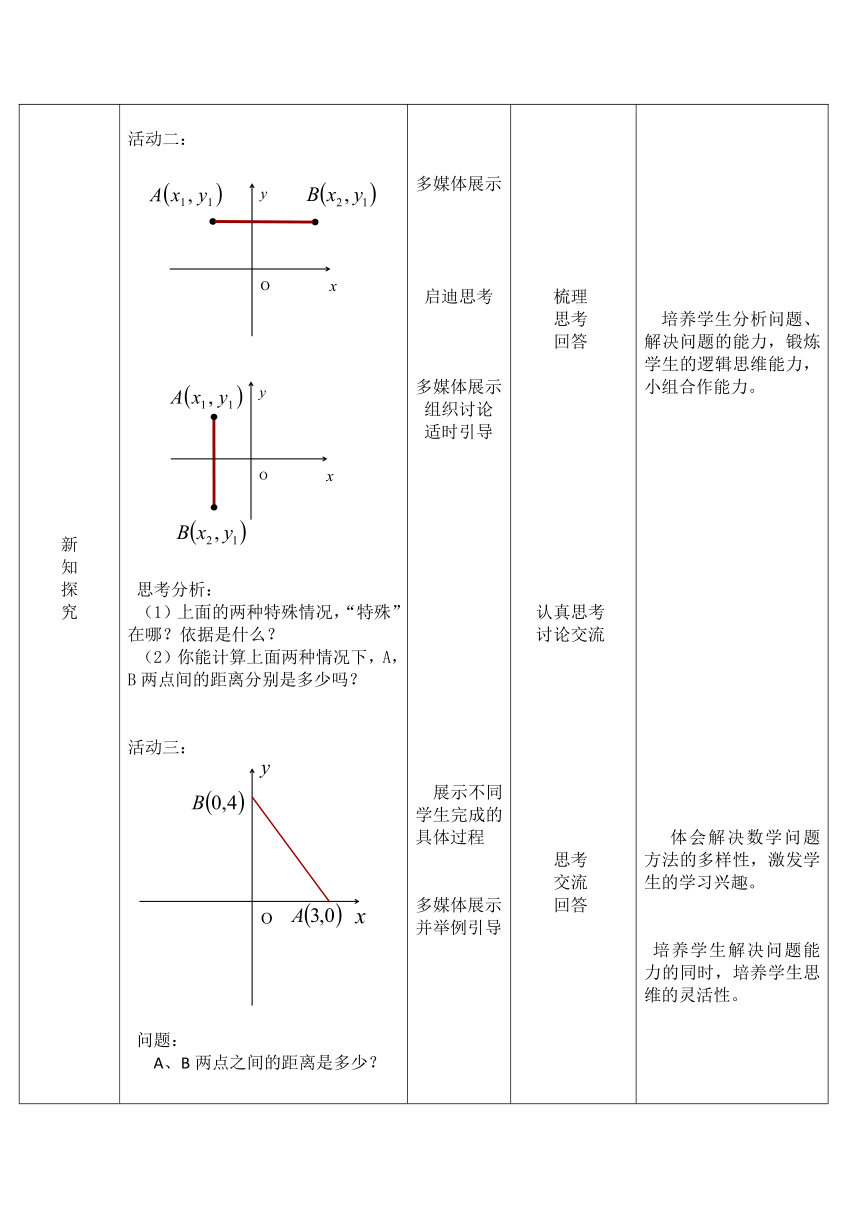
) 思考分析: (1)上面的两种特殊情况,“特殊”在哪?依据是什么? (2)你能计算上面两种情况下,A,B两点间的距离分别是多少吗? (
O
y
x
)活动三: 问题: A、B两点之间的距离是多少? 多媒体展示 启迪思考 多媒体展示 组织讨论 适时引导 展示不同学生完成的具体过程 多媒体展示 并举例引导 梳理 思考 回答 认真思考 讨论交流 思考 交流 回答 培养学生分析问题、解决问题的能力,锻炼学生的逻辑思维能力,小组合作能力。 体会解决数学问题方法的多样性,激发学生的学习兴趣。 培养学生解决问题能力的同时,培养学生思维的灵活性。
新 知 探 究 (
O
y
x
)活动四: 讨论交流 : 如何计算A,B两点之间的距离? 活动五: (
O
y
x
) 思考分析: 对于坐标平面内的任意两点A,B,如何用它们的坐标表示它们之间的距离? 启迪思维 组织讨论 参与指导 探索思考 交流合作 认真思考 讨论交流 合作解决问题 培养学生动手能力,增强合作意识,渗透辩证唯物主义。 培养学生分析问题,解决问题的能力,锻炼学生的逻辑思维能力,小组合作能力
巩 固 练 习 1、求下列两点之间的距离: (1)A(-1,2),B(-5,-6) (2)A(1,-5),B(7,3) 2、有两艘船在海上航行,测得两船的位置分别是(30,50),(105,150),求两船之间的距离。 引导练习 启发解题 认真思考 口述回答 进一步巩固新知,培养学生解决问题的能力能力,并理解数学来源于生活、服务于生活
课 堂 小 结 通过本节课学习,你有什么收获? 点拨 评价 甄别 总结 分享 质疑 梳理学习过程,总结学习规律,巩固目标的达成。
布 置 作 业 必做题: 1.求下列两点之间的距离: (1)A(-1,0),B(2,3) (2)A(4,3) ,B(7,-1) 2.已知△ABC的三个顶点是A(-2,0),B(2,0),C(1, ),试判断△ABC的形状。 选做题: 坐标平面内有一点A(2, ),O为原点,在x轴上找一点B,使以O,A,B为顶点的三角形为等腰三角形,写出点B的坐标。 精选练习 课外探究 分层实施 检验遗漏与不足的同时,让不同的学生得到不同的发展
教 学 反 思 线段的垂直平分线在几何作图,证明,计算中都有着十分重要的作用,线段的垂直平分线的性质定理是推证线段相等的重要途径。 在本节设计上,结合教材,对如何导入新课及其他环节都进行了探索,通过一个生活实例调动学生的学习积极性及兴趣,并让学生感受数学理论来源于实践又服务于实践的价值。 教学过程中,我着重引导,让学生积极主动地参与到教学中来,把知识的形成过程转化为亲自参与,发现,探索的过程,充分体现其主体地位的同时,各方面能力得以发展。 课堂上我还注重学习方法的培养,让学生养成良好的学习习惯,积累学习经验。 对于课堂中的生成问题我关注不够,未及时抓住学生的闪光点,及时表扬。在今后的教学中,我将关注教学生成,关注课堂中的每个瞬间,引导学生用数学知识解决生活问题。
版本 沪科版 授课教师
教 学 目 标 知识与技能: 掌握两点间的距离公式及其运用,以及会用坐标公式求出相应的解。 过程与方法: 通过独立思考和小组交流的方式,学生的独立思考和交流合作的能力得到提高。 情感、态度与价值观: 通过一系列的活动探究过程,体验数学活动充满着探索性和创造性,增强学习数学的学习兴趣。
教学重点 两点间的距离公式及其运用,掌握中点坐标的公式
教学难点 两点间的距离公式和中点坐标公式的推导
教学准备 多媒体、导学案
教学过程
环节设计 教学内容 教师活动 学生活动 设计意图
复 习 引 入 1、前面咱们刚刚学习了勾股定理及其逆定理,同学们还能复述这两个定理吗? 2、在前面学习的基础上,今天我们一起来探究平面内两点之间的距离。 复习引入 互动交流 积极回顾 认真回答 通过复习回顾,创设问题情境,调动学生学习兴趣和积极性。
新 知 探 究 活动一: (
B
) (
O
) (
A
) 如果数轴上的点A,B分别表示数 , ,A,B两点间的距离如何表示? 多媒体展示 思考 回答 为新课学习铺垫
新 知 探 究 活动二: (
O
y
x
) (
O
y
x
) 思考分析: (1)上面的两种特殊情况,“特殊”在哪?依据是什么? (2)你能计算上面两种情况下,A,B两点间的距离分别是多少吗? (
O
y
x
)活动三: 问题: A、B两点之间的距离是多少? 多媒体展示 启迪思考 多媒体展示 组织讨论 适时引导 展示不同学生完成的具体过程 多媒体展示 并举例引导 梳理 思考 回答 认真思考 讨论交流 思考 交流 回答 培养学生分析问题、解决问题的能力,锻炼学生的逻辑思维能力,小组合作能力。 体会解决数学问题方法的多样性,激发学生的学习兴趣。 培养学生解决问题能力的同时,培养学生思维的灵活性。
新 知 探 究 (
O
y
x
)活动四: 讨论交流 : 如何计算A,B两点之间的距离? 活动五: (
O
y
x
) 思考分析: 对于坐标平面内的任意两点A,B,如何用它们的坐标表示它们之间的距离? 启迪思维 组织讨论 参与指导 探索思考 交流合作 认真思考 讨论交流 合作解决问题 培养学生动手能力,增强合作意识,渗透辩证唯物主义。 培养学生分析问题,解决问题的能力,锻炼学生的逻辑思维能力,小组合作能力
巩 固 练 习 1、求下列两点之间的距离: (1)A(-1,2),B(-5,-6) (2)A(1,-5),B(7,3) 2、有两艘船在海上航行,测得两船的位置分别是(30,50),(105,150),求两船之间的距离。 引导练习 启发解题 认真思考 口述回答 进一步巩固新知,培养学生解决问题的能力能力,并理解数学来源于生活、服务于生活
课 堂 小 结 通过本节课学习,你有什么收获? 点拨 评价 甄别 总结 分享 质疑 梳理学习过程,总结学习规律,巩固目标的达成。
布 置 作 业 必做题: 1.求下列两点之间的距离: (1)A(-1,0),B(2,3) (2)A(4,3) ,B(7,-1) 2.已知△ABC的三个顶点是A(-2,0),B(2,0),C(1, ),试判断△ABC的形状。 选做题: 坐标平面内有一点A(2, ),O为原点,在x轴上找一点B,使以O,A,B为顶点的三角形为等腰三角形,写出点B的坐标。 精选练习 课外探究 分层实施 检验遗漏与不足的同时,让不同的学生得到不同的发展
教 学 反 思 线段的垂直平分线在几何作图,证明,计算中都有着十分重要的作用,线段的垂直平分线的性质定理是推证线段相等的重要途径。 在本节设计上,结合教材,对如何导入新课及其他环节都进行了探索,通过一个生活实例调动学生的学习积极性及兴趣,并让学生感受数学理论来源于实践又服务于实践的价值。 教学过程中,我着重引导,让学生积极主动地参与到教学中来,把知识的形成过程转化为亲自参与,发现,探索的过程,充分体现其主体地位的同时,各方面能力得以发展。 课堂上我还注重学习方法的培养,让学生养成良好的学习习惯,积累学习经验。 对于课堂中的生成问题我关注不够,未及时抓住学生的闪光点,及时表扬。在今后的教学中,我将关注教学生成,关注课堂中的每个瞬间,引导学生用数学知识解决生活问题。
