华师大版数学七年级下册同步课件:10.2.2 平移的特征(共24张PPT)
文档属性
| 名称 | 华师大版数学七年级下册同步课件:10.2.2 平移的特征(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1019.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-25 21:52:52 | ||
图片预览



文档简介
(共24张PPT)
第10章 轴对称、平移与旋转
10.2.2 平移的特征
复习导入
A
B
C
D
E
F
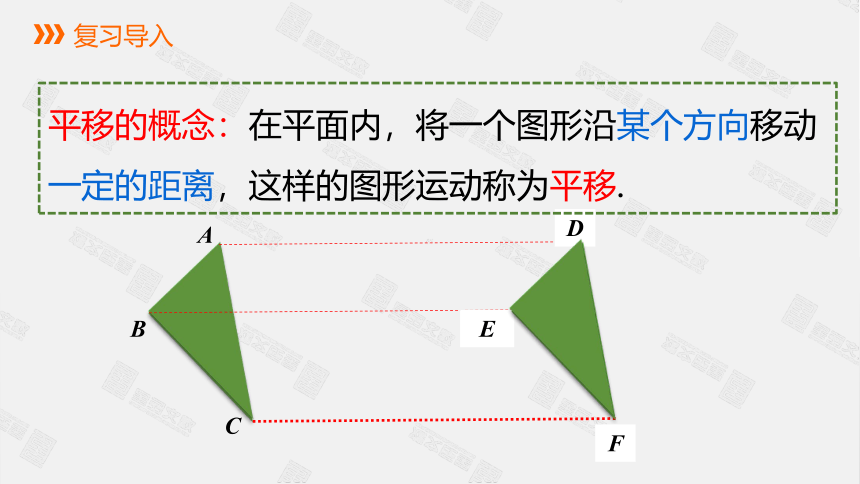
平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
平移改变的是图形的位置,不改变图形的形状和大小。
平移前后对应点、对应线段以及对应角之间在做怎样的变化呢?
获取新知
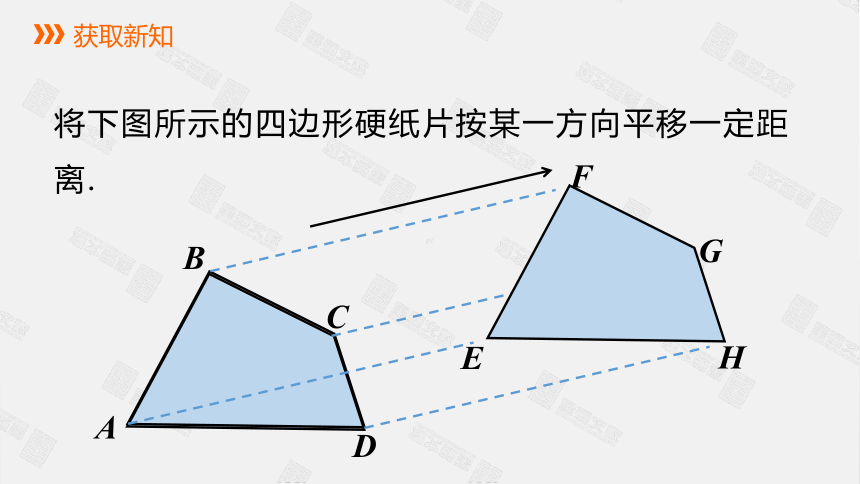
将下图所示的四边形硬纸片按某一方向平移一定距离.
A
B
C
D
E
F
G
H
A
B
C
D
E
F
G
H
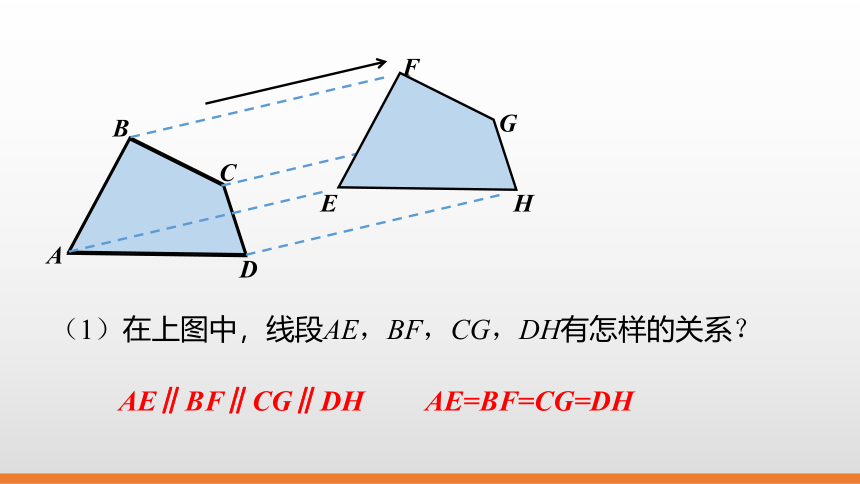
(1)在上图中,线段AE,BF,CG,DH有怎样的关系?
AE∥BF∥CG∥DH
AE=BF=CG=DH
A
B
C
D
E
F
G
H
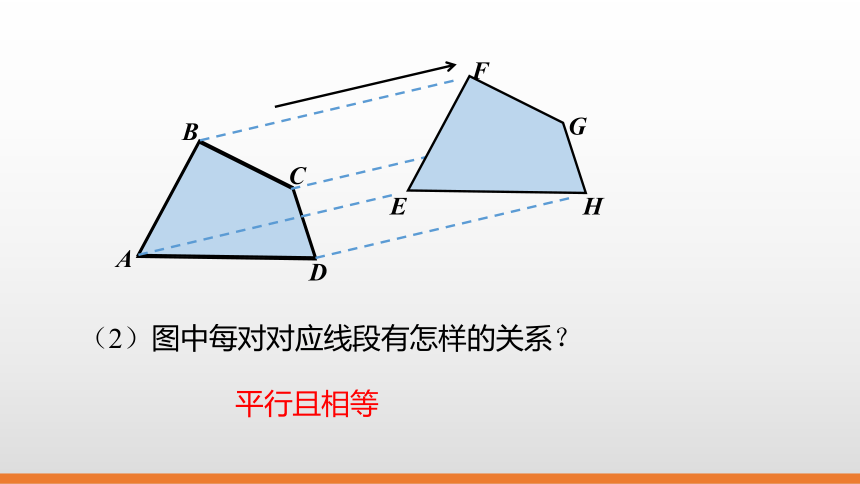
(2)图中每对对应线段有怎样的关系?
平行且相等
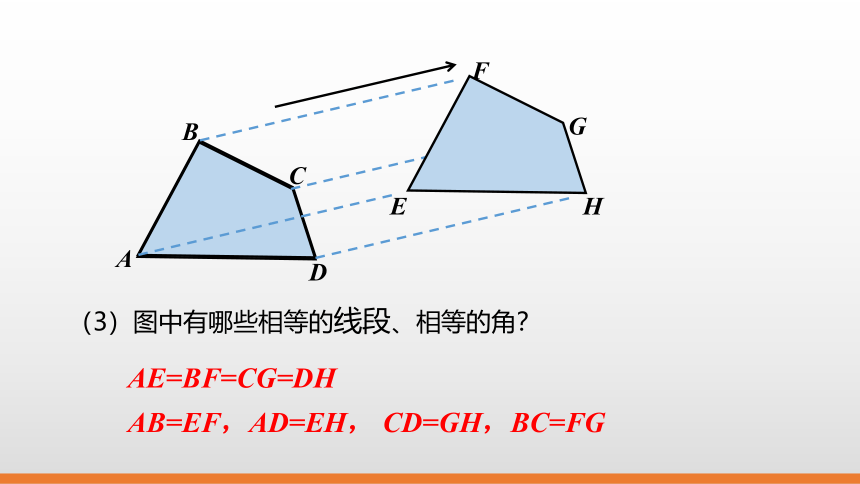
(3)图中有哪些相等的线段、相等的角?
A
B
C
D
E
F
G
H
AE=BF=CG=DH
AB=EF,AD=EH, CD=GH,BC=FG
平移的性质:
一个图形和它经过平移所得的图形:
1.对应点所连的线段平行(或在一条直线上)且相等;
2.对应线段平行(或在一条直线上)且相等;
3.对应角相等;
4.平移前后图形是全等关系
试一试
A
B
C
F
D
E
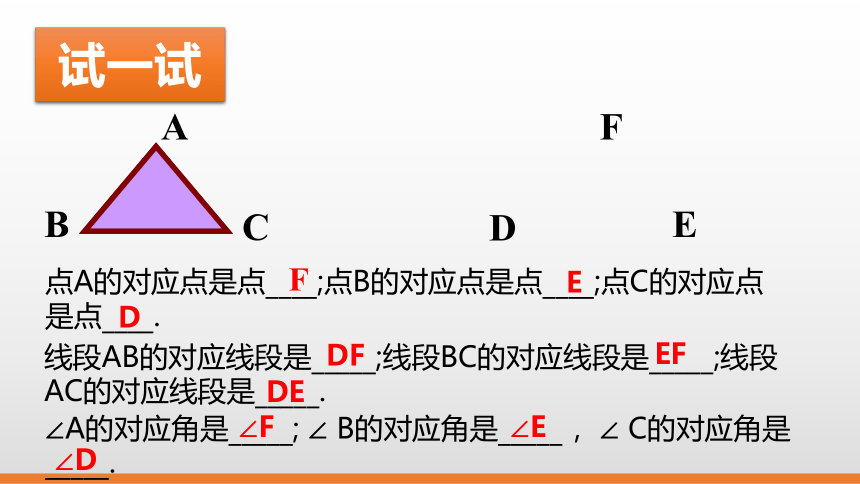
点A的对应点是点____;点B的对应点是点____;点C的对应点是点____.
线段AB的对应线段是_____;线段BC的对应线段是_____;线段AC的对应线段是_____.
∠A的对应角是_____; ∠ B的对应角是_____ ,∠ C的对应角是_____.
F
D
E
DF
EF
∠F
∠D
∠E
DE
如图,观察△ABC和△A′B′C′的关系.思考:
(1) △ABC是沿着什么方向移动多少距离得到△A′B′C′的?
(2)线段AA′、BB′、CC′有怎样的位置关系?
(3)图中有哪些相等的线段、相等的角?
C
B
A
P
Q
B′
A′
C′
合作探究
如图,观察△ABC和△A′B′C′的关系.思考:
(1) △ABC是沿着什么方向移动多少距离得到△A′B′C′的?
B
A
C
P
Q
△ABC沿着PQ的方向平移PQ的长度到 △A′B′C′的位置.
如图,观察△ABC和△A′B′C′的关系.思考:
(2)线段AA′、BB′、CC′有怎样的位置关系?
B
A
C
P
Q
A
A′
B
B′
C
C′
AA′∥____ ∥ ____
AA′=____=____
BB′
CC′
CC′
BB′
平移后对应点的连线平行且相等.
思考:如图,观察△ABC和△A′B′C′的关系.
(3)图中有哪些相等的线段、相等的角?
C
B
A
P
Q
B′
A′
C′
AB=A′B′,AC=A′C′ , BC=B′C′ , AA′=BB′=CC′
∠A= ∠A′, ∠B=∠B′, ∠C= ∠C′
试一试:将图中的△A′B′C′沿RS方向移动到△A″B″C″ 的位置,平移的距离为线段RS的长度.
R
S
C′
B′
A′
注意:在平移过程中,对应点所连的线段也可能一条直线上.
A
B
C
(1)先找到对应点;
(2)连结两个对应点;
(3)平移的方向就是点A到点A′的方向.
(4)平移的距离就是线段AA′的长度,约为2 cm.
例 如图所示,△ABC经过平移到△A′B′C′的位置,指出平移的方向,并量出平移的距离.
例题讲解
在如下图所示的方格纸中,画出将图中的△ABC向右平移4格后的△A′B′C′,然后再画出将△A′B′C′向上平移3格后的△A′′B′′C′′.△A′′B′′C′′是否可以看成是△ABC经过一次平移而得到的呢?如果是,那么平移的方向和距离分别是什么呢?
A
B
C
A′
B′
C′
A′′
B′′
C′′
试一试
△A′′B′′C′′可以看成是△ABC经过一次平移而得到的图形,它的平移方向是由对应点A到对应点A′′的方向,它的平移距离是线段AA′′的长度.
结论:多次平移相当于一次平移.
A
B
C
A′
B′
C′
A′′
B′′
C′′
1. 如图,将△ABC平移到△DEF的位置,则下列说法:
①AB∥DE,AD=CF=BE;②∠ACB=∠DEF;③平移的方向是点C到点E的方向;④平移距离为线段BE的长.其中说法正确的有( )
A.1个 B.2个 C.3个 D.4个
B
随堂演练
2. 如图,将△ABC沿射线BC方向平移7 cm,得到△A'B'C',若B'C=3 cm,则B'C'= cm.
4
3. 如图,将△ABC沿射线AB的方向平移到△DEF的位置,点A,B,C的对应点分别为点D,E,F,若∠ABC=75°,则∠CFE= °.
105
4. 如图,已知△ABD,AC平分∠DAB,与BD交于点C,平移△ABC,
使点C移动到点D,点B的对应点是E,点A的对应点是F.
(1)在图中画出平移后得到的△FED;
(2)若∠DAB=72°,EF与AD相交于点H,
则∠FDA= °,∠DHF= °.
解:(1)如图所示,△FED即为所求.
(2)∵∠DAB=72°,AC平分∠DAB,
∴∠DAC=36°.
∵△ABC平移得到△FED,
∴DF∥AC,EF∥AB,
∴∠FDA=∠DAC=36°,∠FHA=∠DAB=72°,
∴∠DHF=108°.
故答案为36,108.
知识点一 平移的特征
平行并且相等
相等
平行
相等
课堂小结
知识点二 平移作图
(1)根据作图要求,找出平移的方向和平移的距离;(2)找出构成图形的关键点,根据平移的特征作出关键点的对应点;(3)按原图形的连结方式连结各关键点的对应点,注意根据需要标注字母
第10章 轴对称、平移与旋转
10.2.2 平移的特征
复习导入
A
B
C
D
E
F
平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
平移改变的是图形的位置,不改变图形的形状和大小。
平移前后对应点、对应线段以及对应角之间在做怎样的变化呢?
获取新知
将下图所示的四边形硬纸片按某一方向平移一定距离.
A
B
C
D
E
F
G
H
A
B
C
D
E
F
G
H
(1)在上图中,线段AE,BF,CG,DH有怎样的关系?
AE∥BF∥CG∥DH
AE=BF=CG=DH
A
B
C
D
E
F
G
H
(2)图中每对对应线段有怎样的关系?
平行且相等
(3)图中有哪些相等的线段、相等的角?
A
B
C
D
E
F
G
H
AE=BF=CG=DH
AB=EF,AD=EH, CD=GH,BC=FG
平移的性质:
一个图形和它经过平移所得的图形:
1.对应点所连的线段平行(或在一条直线上)且相等;
2.对应线段平行(或在一条直线上)且相等;
3.对应角相等;
4.平移前后图形是全等关系
试一试
A
B
C
F
D
E
点A的对应点是点____;点B的对应点是点____;点C的对应点是点____.
线段AB的对应线段是_____;线段BC的对应线段是_____;线段AC的对应线段是_____.
∠A的对应角是_____; ∠ B的对应角是_____ ,∠ C的对应角是_____.
F
D
E
DF
EF
∠F
∠D
∠E
DE
如图,观察△ABC和△A′B′C′的关系.思考:
(1) △ABC是沿着什么方向移动多少距离得到△A′B′C′的?
(2)线段AA′、BB′、CC′有怎样的位置关系?
(3)图中有哪些相等的线段、相等的角?
C
B
A
P
Q
B′
A′
C′
合作探究
如图,观察△ABC和△A′B′C′的关系.思考:
(1) △ABC是沿着什么方向移动多少距离得到△A′B′C′的?
B
A
C
P
Q
△ABC沿着PQ的方向平移PQ的长度到 △A′B′C′的位置.
如图,观察△ABC和△A′B′C′的关系.思考:
(2)线段AA′、BB′、CC′有怎样的位置关系?
B
A
C
P
Q
A
A′
B
B′
C
C′
AA′∥____ ∥ ____
AA′=____=____
BB′
CC′
CC′
BB′
平移后对应点的连线平行且相等.
思考:如图,观察△ABC和△A′B′C′的关系.
(3)图中有哪些相等的线段、相等的角?
C
B
A
P
Q
B′
A′
C′
AB=A′B′,AC=A′C′ , BC=B′C′ , AA′=BB′=CC′
∠A= ∠A′, ∠B=∠B′, ∠C= ∠C′
试一试:将图中的△A′B′C′沿RS方向移动到△A″B″C″ 的位置,平移的距离为线段RS的长度.
R
S
C′
B′
A′
注意:在平移过程中,对应点所连的线段也可能一条直线上.
A
B
C
(1)先找到对应点;
(2)连结两个对应点;
(3)平移的方向就是点A到点A′的方向.
(4)平移的距离就是线段AA′的长度,约为2 cm.
例 如图所示,△ABC经过平移到△A′B′C′的位置,指出平移的方向,并量出平移的距离.
例题讲解
在如下图所示的方格纸中,画出将图中的△ABC向右平移4格后的△A′B′C′,然后再画出将△A′B′C′向上平移3格后的△A′′B′′C′′.△A′′B′′C′′是否可以看成是△ABC经过一次平移而得到的呢?如果是,那么平移的方向和距离分别是什么呢?
A
B
C
A′
B′
C′
A′′
B′′
C′′
试一试
△A′′B′′C′′可以看成是△ABC经过一次平移而得到的图形,它的平移方向是由对应点A到对应点A′′的方向,它的平移距离是线段AA′′的长度.
结论:多次平移相当于一次平移.
A
B
C
A′
B′
C′
A′′
B′′
C′′
1. 如图,将△ABC平移到△DEF的位置,则下列说法:
①AB∥DE,AD=CF=BE;②∠ACB=∠DEF;③平移的方向是点C到点E的方向;④平移距离为线段BE的长.其中说法正确的有( )
A.1个 B.2个 C.3个 D.4个
B
随堂演练
2. 如图,将△ABC沿射线BC方向平移7 cm,得到△A'B'C',若B'C=3 cm,则B'C'= cm.
4
3. 如图,将△ABC沿射线AB的方向平移到△DEF的位置,点A,B,C的对应点分别为点D,E,F,若∠ABC=75°,则∠CFE= °.
105
4. 如图,已知△ABD,AC平分∠DAB,与BD交于点C,平移△ABC,
使点C移动到点D,点B的对应点是E,点A的对应点是F.
(1)在图中画出平移后得到的△FED;
(2)若∠DAB=72°,EF与AD相交于点H,
则∠FDA= °,∠DHF= °.
解:(1)如图所示,△FED即为所求.
(2)∵∠DAB=72°,AC平分∠DAB,
∴∠DAC=36°.
∵△ABC平移得到△FED,
∴DF∥AC,EF∥AB,
∴∠FDA=∠DAC=36°,∠FHA=∠DAB=72°,
∴∠DHF=108°.
故答案为36,108.
知识点一 平移的特征
平行并且相等
相等
平行
相等
课堂小结
知识点二 平移作图
(1)根据作图要求,找出平移的方向和平移的距离;(2)找出构成图形的关键点,根据平移的特征作出关键点的对应点;(3)按原图形的连结方式连结各关键点的对应点,注意根据需要标注字母
