华师大版数学七年级下册同步课件:10.3.1 图形的旋转&10.3.2 旋转的特征(共26张PPT)
文档属性
| 名称 | 华师大版数学七年级下册同步课件:10.3.1 图形的旋转&10.3.2 旋转的特征(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-25 22:11:01 | ||
图片预览







文档简介
(共26张PPT)
第10章 轴对称、平移与旋转
10.3 旋转
情景导入
(1)上面场景中的转动现象,有什么共同特征?
(2)风力发电机的叶片、钟表的指针在转动过程中,其形状、大小、位置是否发生改变?
悬挂点就叫小球的旋转中心.
转动的角称为旋转角.
转动的方向分为顺时针与逆时针.
单摆小球从由位置P转到位置P’,即绕上面的悬挂点在一个平面上转动.像这样的运动,就叫做旋转。
获取新知
旋转中心在旋转中保持不动,图形的旋转由旋转中心、旋转的角度和方形所决定
旋转中心
旋转角
旋转方向
必须明确
确定一次图形的旋转时,
旋转与平移类似,也属于全等变换,即运动前后改变的是图形的位置,图形的形状和大小都不变
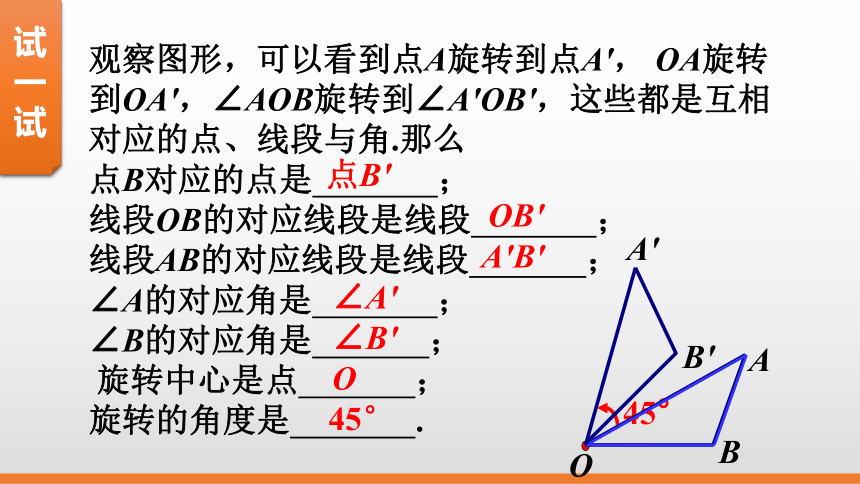
观察图形,可以看到点A旋转到点A′, OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段与角.那么
点B对应的点是 ;
线段OB的对应线段是线段 ;
线段AB的对应线段是线段 ;
∠A的对应角是 ;
∠B的对应角是 ;
旋转中心是点 ;
旋转的角度是 .
45°
A′
B′
O
A
B
点B′
OB′
A′B′
∠A′
∠B′
O
45°
试一试
想一想
45°
A′
B′
O
A
B
D
△AOB的边OB的中点D的对应点在哪里?
做一做
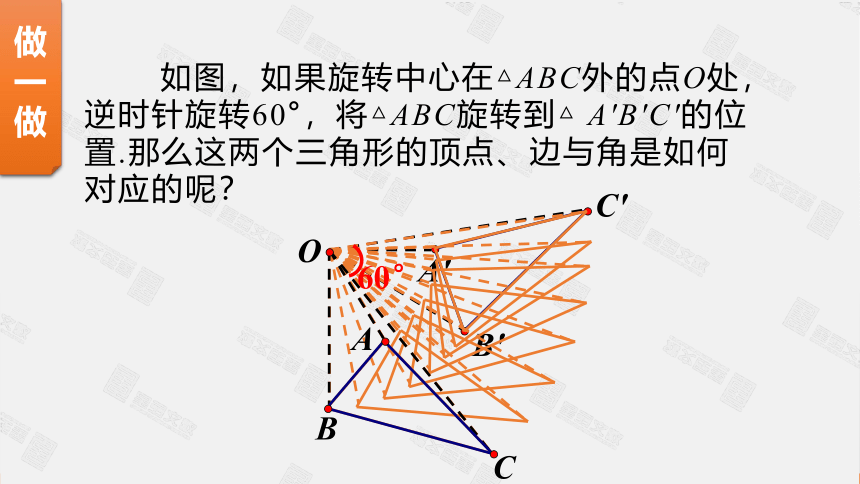
如图,如果旋转中心在△ABC外的点O处,逆时针旋转60°,将△ABC旋转到△ A′B′C′的位置.那么这两个三角形的顶点、边与角是如何对应的呢?
A'
B'
C'
O
60°
B
C
A
在图中,旋转中心是点O,点A、 B、 C绕点O逆时针旋转60°的对应点是A′、 B′、 C′,而且
OA= , OB= , OC= ;
AB= , BC= , CA= ;
∠CAB= , ∠ABC= , ∠BCA= .
OA′
OB′
OC′
A′B′
B′C′
C′A′
∠C′A′B′
∠A′B′C′
∠B′C′A′
A'
B'
C'
O
60°
B
C
A
(1)旋转不改变图形的大小和形状.
(2)图形上的每一点都绕旋转中心沿
相同方向转动了相同的角度.
(3)任意一对对应点与旋转中心的连
线所成的角度都是旋转角.
(4)对应点到旋转中心的距离相等.
( 5 )对应线段相等,对应角相等.
旋转基本性质
例题讲解
例1:如图,△ABC是等边三角形,D是BC上一点,△ABD经过逆时针旋转后到达△ACE的位置.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后点M转到了什么位置?
B
C
A
D
E
M
解:(1)旋转中心是点A;
(2)旋转了60°;
(3)点M转到了AC的中点位置上.
例2:如图,点M是线段AB上一点,将线段AB绕着点M顺时针旋转90°,旋转后的线段与原线段的位置有何关系?如果逆时针旋转90°呢?
B
A
M
解:(1)顺时针旋转90°,A′B′与AB互相垂直.
B
A
M
A′
B′
解:(2)逆时针旋转90°,A′′B′′与AB互相垂直.
B
A
M
B′′
A′′
观察图1与图2,你能发现有哪些线段相等?有哪些角相等?
图1
图2
我们可以看到,在图1中,线段OA、OB都是绕
点O逆时针旋转45°到对应线段OA′、OB′,而且
OA = OA',OB = OB',AB = A′B′;
∠AOB = ∠A′OB′ ,∠A=∠A′,∠B=∠B′ .
在图2中,旋转中心是点O,点A、B、C都是绕
点O逆时针旋转60°到对应点A′、B′、C′,而且
OA =_____,OB =_____,OC =_____;
AB =_____,BC =_____,CA =_____;
∠CAB =_____,∠ABC =_____,∠BCA =_____.
这就是图形旋转的特征:图形中每一点都绕着旋
转中心按同一旋转方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状与大小不变.
随堂演练
1.下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
C
2. 如图,△ABC按顺时针方向旋转到△ADE的位置,以下关于旋转中心和对应点的说法正确的是( )
A.点A是旋转中心,点B和点E是对应点
B.点C是旋转中心,点B和点D是对应点
C.点A是旋转中心,点C和点E是对应点
D.点D是旋转中心,点A和点D是对应点
C
3. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( )
A.55° B.60° C.65° D.70°
C
4. 如图,△ABC绕点A逆时针旋转30°得到△ADE,AB=5 cm,BC=8 cm,∠BAC=130°,则AD= = cm,
DE= = cm,∠EAC=∠ = °.
AB
5
BC
8
BAD
30
5. 如图,Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD.把 △ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m= ________.
80或120
6. 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B两点不重合),连接CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连接DE交BC于点F,连接BE.
(1)求证:△ACD≌△BCE;
(2)当AD=BF时,求∠BEF的度数.
(1)证明:由题意可知CD=CE,∠DCE=90°.
∵∠ACB=90°,∠ACD=∠ACB-∠DCB,∠BCE=∠DCE-∠DCB,
∴∠ACD=∠BCE.
在△ACD与△BCE中,
∵AC=BC,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE.
(2)∵∠ACB=90°,AC=BC,
∴∠A=45°.
由(1)知△ACD≌△BCE,
∴∠CBE=∠A=45°,AD=BE.
∵AD=BF,∴BE=BF,
∴∠BEF= ×(180°-45°)=67.5°.
课堂小结
旋转
定义
三要素:旋转中心,旋转方向和旋转角度
性质
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角
第10章 轴对称、平移与旋转
10.3 旋转
情景导入
(1)上面场景中的转动现象,有什么共同特征?
(2)风力发电机的叶片、钟表的指针在转动过程中,其形状、大小、位置是否发生改变?
悬挂点就叫小球的旋转中心.
转动的角称为旋转角.
转动的方向分为顺时针与逆时针.
单摆小球从由位置P转到位置P’,即绕上面的悬挂点在一个平面上转动.像这样的运动,就叫做旋转。
获取新知
旋转中心在旋转中保持不动,图形的旋转由旋转中心、旋转的角度和方形所决定
旋转中心
旋转角
旋转方向
必须明确
确定一次图形的旋转时,
旋转与平移类似,也属于全等变换,即运动前后改变的是图形的位置,图形的形状和大小都不变
观察图形,可以看到点A旋转到点A′, OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段与角.那么
点B对应的点是 ;
线段OB的对应线段是线段 ;
线段AB的对应线段是线段 ;
∠A的对应角是 ;
∠B的对应角是 ;
旋转中心是点 ;
旋转的角度是 .
45°
A′
B′
O
A
B
点B′
OB′
A′B′
∠A′
∠B′
O
45°
试一试
想一想
45°
A′
B′
O
A
B
D
△AOB的边OB的中点D的对应点在哪里?
做一做
如图,如果旋转中心在△ABC外的点O处,逆时针旋转60°,将△ABC旋转到△ A′B′C′的位置.那么这两个三角形的顶点、边与角是如何对应的呢?
A'
B'
C'
O
60°
B
C
A
在图中,旋转中心是点O,点A、 B、 C绕点O逆时针旋转60°的对应点是A′、 B′、 C′,而且
OA= , OB= , OC= ;
AB= , BC= , CA= ;
∠CAB= , ∠ABC= , ∠BCA= .
OA′
OB′
OC′
A′B′
B′C′
C′A′
∠C′A′B′
∠A′B′C′
∠B′C′A′
A'
B'
C'
O
60°
B
C
A
(1)旋转不改变图形的大小和形状.
(2)图形上的每一点都绕旋转中心沿
相同方向转动了相同的角度.
(3)任意一对对应点与旋转中心的连
线所成的角度都是旋转角.
(4)对应点到旋转中心的距离相等.
( 5 )对应线段相等,对应角相等.
旋转基本性质
例题讲解
例1:如图,△ABC是等边三角形,D是BC上一点,△ABD经过逆时针旋转后到达△ACE的位置.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后点M转到了什么位置?
B
C
A
D
E
M
解:(1)旋转中心是点A;
(2)旋转了60°;
(3)点M转到了AC的中点位置上.
例2:如图,点M是线段AB上一点,将线段AB绕着点M顺时针旋转90°,旋转后的线段与原线段的位置有何关系?如果逆时针旋转90°呢?
B
A
M
解:(1)顺时针旋转90°,A′B′与AB互相垂直.
B
A
M
A′
B′
解:(2)逆时针旋转90°,A′′B′′与AB互相垂直.
B
A
M
B′′
A′′
观察图1与图2,你能发现有哪些线段相等?有哪些角相等?
图1
图2
我们可以看到,在图1中,线段OA、OB都是绕
点O逆时针旋转45°到对应线段OA′、OB′,而且
OA = OA',OB = OB',AB = A′B′;
∠AOB = ∠A′OB′ ,∠A=∠A′,∠B=∠B′ .
在图2中,旋转中心是点O,点A、B、C都是绕
点O逆时针旋转60°到对应点A′、B′、C′,而且
OA =_____,OB =_____,OC =_____;
AB =_____,BC =_____,CA =_____;
∠CAB =_____,∠ABC =_____,∠BCA =_____.
这就是图形旋转的特征:图形中每一点都绕着旋
转中心按同一旋转方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状与大小不变.
随堂演练
1.下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
C
2. 如图,△ABC按顺时针方向旋转到△ADE的位置,以下关于旋转中心和对应点的说法正确的是( )
A.点A是旋转中心,点B和点E是对应点
B.点C是旋转中心,点B和点D是对应点
C.点A是旋转中心,点C和点E是对应点
D.点D是旋转中心,点A和点D是对应点
C
3. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( )
A.55° B.60° C.65° D.70°
C
4. 如图,△ABC绕点A逆时针旋转30°得到△ADE,AB=5 cm,BC=8 cm,∠BAC=130°,则AD= = cm,
DE= = cm,∠EAC=∠ = °.
AB
5
BC
8
BAD
30
5. 如图,Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD.把 △ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m= ________.
80或120
6. 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B两点不重合),连接CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连接DE交BC于点F,连接BE.
(1)求证:△ACD≌△BCE;
(2)当AD=BF时,求∠BEF的度数.
(1)证明:由题意可知CD=CE,∠DCE=90°.
∵∠ACB=90°,∠ACD=∠ACB-∠DCB,∠BCE=∠DCE-∠DCB,
∴∠ACD=∠BCE.
在△ACD与△BCE中,
∵AC=BC,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE.
(2)∵∠ACB=90°,AC=BC,
∴∠A=45°.
由(1)知△ACD≌△BCE,
∴∠CBE=∠A=45°,AD=BE.
∵AD=BF,∴BE=BF,
∴∠BEF= ×(180°-45°)=67.5°.
课堂小结
旋转
定义
三要素:旋转中心,旋转方向和旋转角度
性质
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角
