5.2.2导数的四则运算法则 学案——2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册
文档属性
| 名称 | 5.2.2导数的四则运算法则 学案——2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册 |

|
|
| 格式 | doc | ||
| 文件大小 | 368.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-25 00:00:00 | ||
图片预览


文档简介
第五章 一元函数的导数及其应用
5.2 导数的运算
5.2.2 导数的四则运算法则
学案
一、学习目标
1. 理解并掌握导数的四则运算法则;
2. 能够综合运用导数公式和导数的四则运算法则求简单函数的导数.
二、基础梳理
对于两个函数和,有如下法则:
_________________;
_________________;
_________________;
_________________.
三、巩固练习
1.若,则( )
A.3 B.8 C. D.
2.函数的图象在点处的切线的倾斜角为( )
A.0 B. C. D.
3.若函数,则等于( )
A.-2 B.-1 C.1 D.0
4.已知,则( )
A.2017 B.2018 C.2019 D.2020
5.曲线在处的切线与坐标轴围成的三角形的面积为( )
A. B. C. D.
6.已知曲线在点处的切线与曲线相切,则a的值为__________.
7.已知函数,若,则实数a的值为_________.
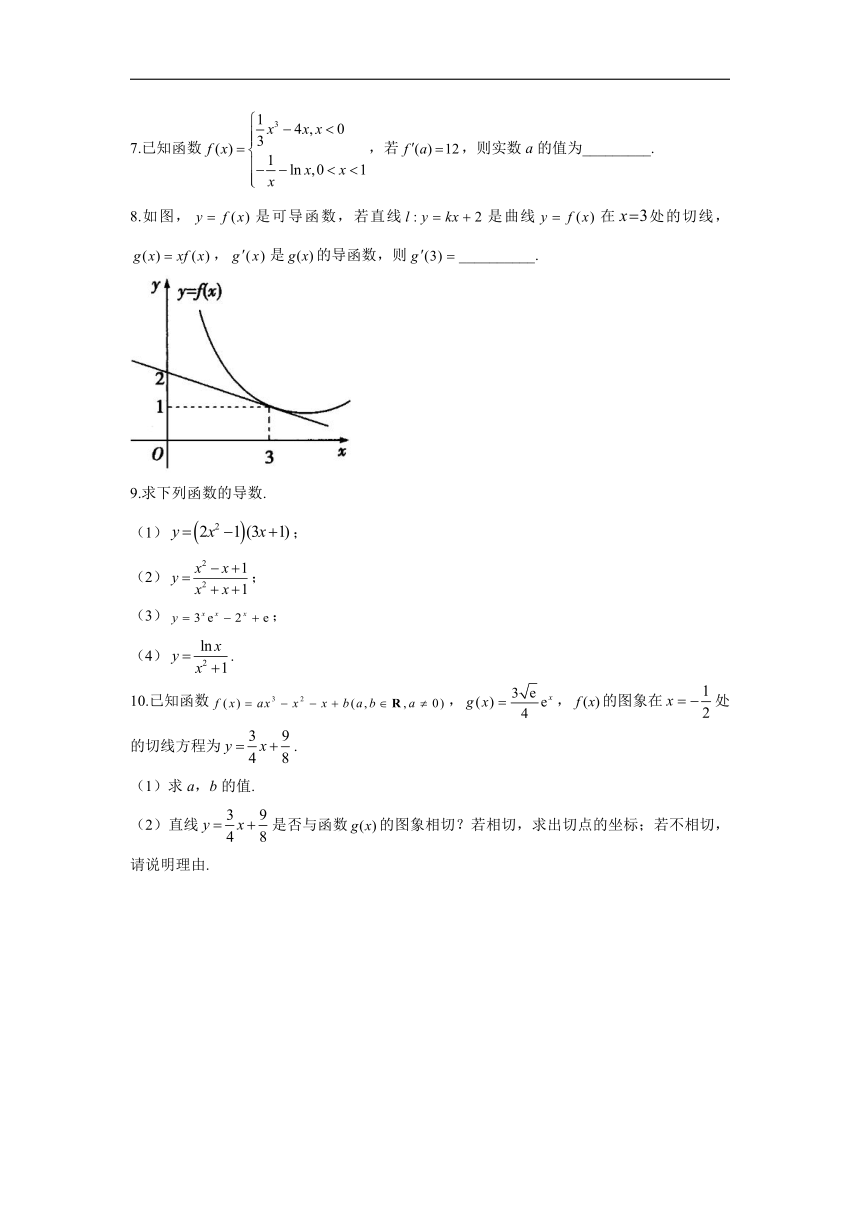
8.如图,是可导函数,若直线是曲线在处的切线,,是的导函数,则__________.
9.求下列函数的导数.
(1);
(2);
(3);
(4).
10.已知函数,,的图象在处的切线方程为.
(1)求a,b的值.
(2)直线是否与函数的图象相切?若相切,求出切点的坐标;若不相切,请说明理由.
参考答案
基础梳理
;;;.
巩固练习
1.答案:B
解析:,把代入得.故选B.
2.答案:B
解析:由题意得,,
所以函数的图象在点处的切线的斜率,则所求的倾斜角为.故选B.
3.答案:C
解析:,.故选C.
4.答案:D
解析:易知,令,得,
则.故选D.
5.答案:B
解析:曲线在点处的切线方程为,与坐标轴的交点坐标分别为,该切线与坐标轴围成的三角形的面积为.故选B.
6.答案:8
解析:由,得,当时,.所以曲线在点处的切线方程为.由,得,又切线与曲线也相切,所以,解得,此时切点坐标为,代入即可求得.
7.答案:或
解析:,若,则或,解得或.
8.答案:0
解析:由题图知,.点在直线l上,,即,,,,则.
9.答案:(1)方法一:,
.
方法二:由导数的乘法法则得
.
(2)根据题意把函数的解析式整理变形可得
,
.
(3)根据求导法则可得
.
(4)根据题意,利用求导的除法法则可得
.
10.答案:(1).
的图象在处的切线方程为,
,即,解得,
又的图象过点,
,解得.
综上,,.
(2)设直线与函数的图象相切于点.
,,解得,
将代入,得点A的坐标是,
故直线与函数的图象相切,切点坐标是.
5.2 导数的运算
5.2.2 导数的四则运算法则
学案
一、学习目标
1. 理解并掌握导数的四则运算法则;
2. 能够综合运用导数公式和导数的四则运算法则求简单函数的导数.
二、基础梳理
对于两个函数和,有如下法则:
_________________;
_________________;
_________________;
_________________.
三、巩固练习
1.若,则( )
A.3 B.8 C. D.
2.函数的图象在点处的切线的倾斜角为( )
A.0 B. C. D.
3.若函数,则等于( )
A.-2 B.-1 C.1 D.0
4.已知,则( )
A.2017 B.2018 C.2019 D.2020
5.曲线在处的切线与坐标轴围成的三角形的面积为( )
A. B. C. D.
6.已知曲线在点处的切线与曲线相切,则a的值为__________.
7.已知函数,若,则实数a的值为_________.
8.如图,是可导函数,若直线是曲线在处的切线,,是的导函数,则__________.
9.求下列函数的导数.
(1);
(2);
(3);
(4).
10.已知函数,,的图象在处的切线方程为.
(1)求a,b的值.
(2)直线是否与函数的图象相切?若相切,求出切点的坐标;若不相切,请说明理由.
参考答案
基础梳理
;;;.
巩固练习
1.答案:B
解析:,把代入得.故选B.
2.答案:B
解析:由题意得,,
所以函数的图象在点处的切线的斜率,则所求的倾斜角为.故选B.
3.答案:C
解析:,.故选C.
4.答案:D
解析:易知,令,得,
则.故选D.
5.答案:B
解析:曲线在点处的切线方程为,与坐标轴的交点坐标分别为,该切线与坐标轴围成的三角形的面积为.故选B.
6.答案:8
解析:由,得,当时,.所以曲线在点处的切线方程为.由,得,又切线与曲线也相切,所以,解得,此时切点坐标为,代入即可求得.
7.答案:或
解析:,若,则或,解得或.
8.答案:0
解析:由题图知,.点在直线l上,,即,,,,则.
9.答案:(1)方法一:,
.
方法二:由导数的乘法法则得
.
(2)根据题意把函数的解析式整理变形可得
,
.
(3)根据求导法则可得
.
(4)根据题意,利用求导的除法法则可得
.
10.答案:(1).
的图象在处的切线方程为,
,即,解得,
又的图象过点,
,解得.
综上,,.
(2)设直线与函数的图象相切于点.
,,解得,
将代入,得点A的坐标是,
故直线与函数的图象相切,切点坐标是.
