2021-2022学年苏科版八年级数学上册 第一章全等三角形讲义
文档属性
| 名称 | 2021-2022学年苏科版八年级数学上册 第一章全等三角形讲义 |

|
|
| 格式 | docx | ||
| 文件大小 | 499.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 08:22:31 | ||
图片预览

文档简介
日期: 时间: 学生姓名:
全等三角形
全等三角形知识点提优
知识点一、全等三角形的概念与性质
1.如图,把沿线段折叠,使点落在点处;若,,,则的度数为( )
A. B. C. D.
2.如图ABC≌,边过点A且平分∠BAC交BC于点D,∠B=26°,=94°,则的度数为( )
A.34° B.40° C.45° D.60°
3.如图,在长方形ABCD中,,.延长BC到点E,使,连结DE,动点P从点B出发,以每秒2个单位长度的速度沿向终点A运动.设点P的运动时间为t秒,当t的值为____________时,和全等.
4.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,己知DE=4,AD=6,则BE的长为 ____________
知识点二、全等三角形的判定
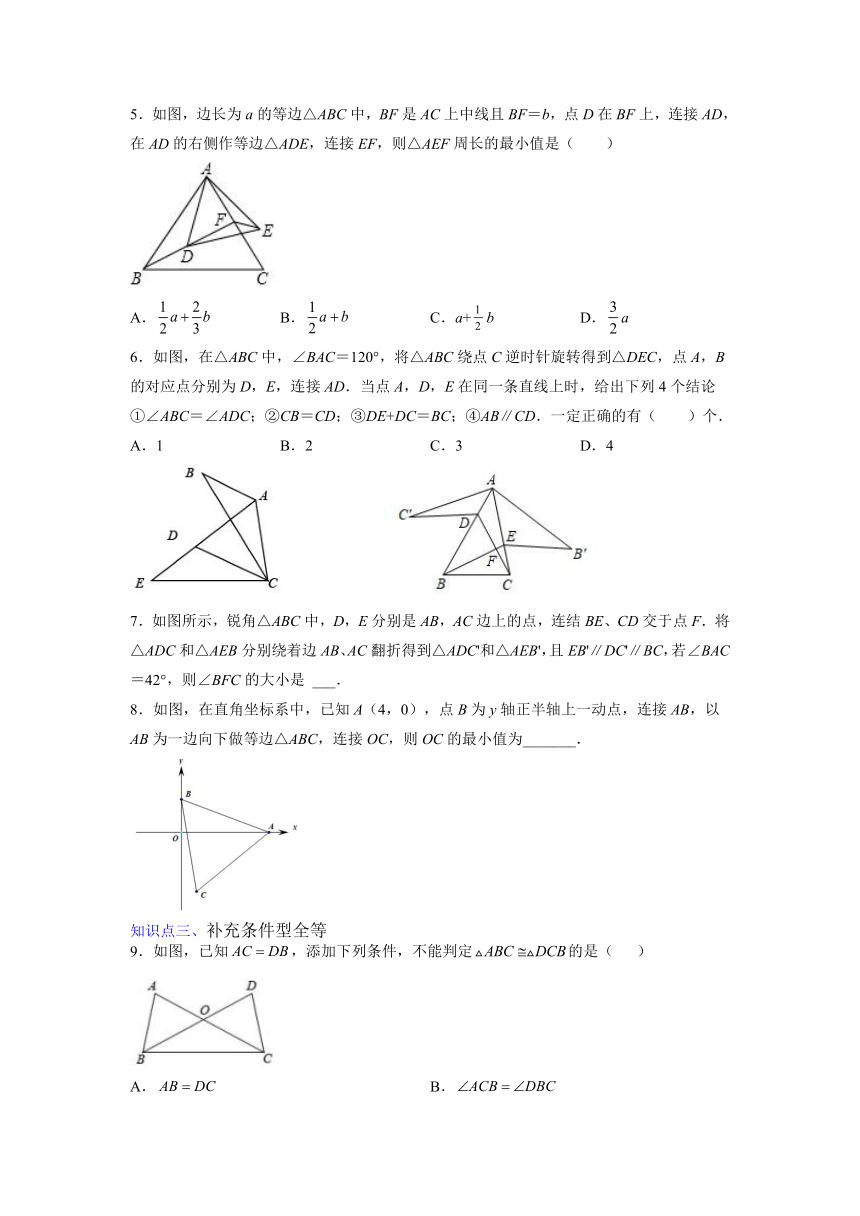
5.如图,边长为a的等边△ABC中,BF是AC上中线且BF=b,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,则△AEF周长的最小值是( )
A. B. C.a+b D.a
6.如图,在△ABC中,∠BAC=120°,将△ABC绕点C逆时针旋转得到△DEC,点A,B的对应点分别为D,E,连接AD.当点A,D,E在同一条直线上时,给出下列4个结论①∠ABC=∠ADC;②CB=CD;③DE+DC=BC;④AB∥CD.一定正确的有( )个.
A.1 B.2 C.3 D.4
7.如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,连结BE、CD交于点F.将△ADC和△AEB分别绕着边AB、AC翻折得到△ADC'和△AEB',且EB'∥DC'∥BC,若∠BAC=42°,则∠BFC的大小是 ___.
8.如图,在直角坐标系中,已知A(4,0),点B为y轴正半轴上一动点,连接AB,以AB为一边向下做等边△ABC,连接OC,则OC的最小值为_______.
知识点三、补充条件型全等
9.如图,已知,添加下列条件,不能判定的是( )
A. B.
C. D.
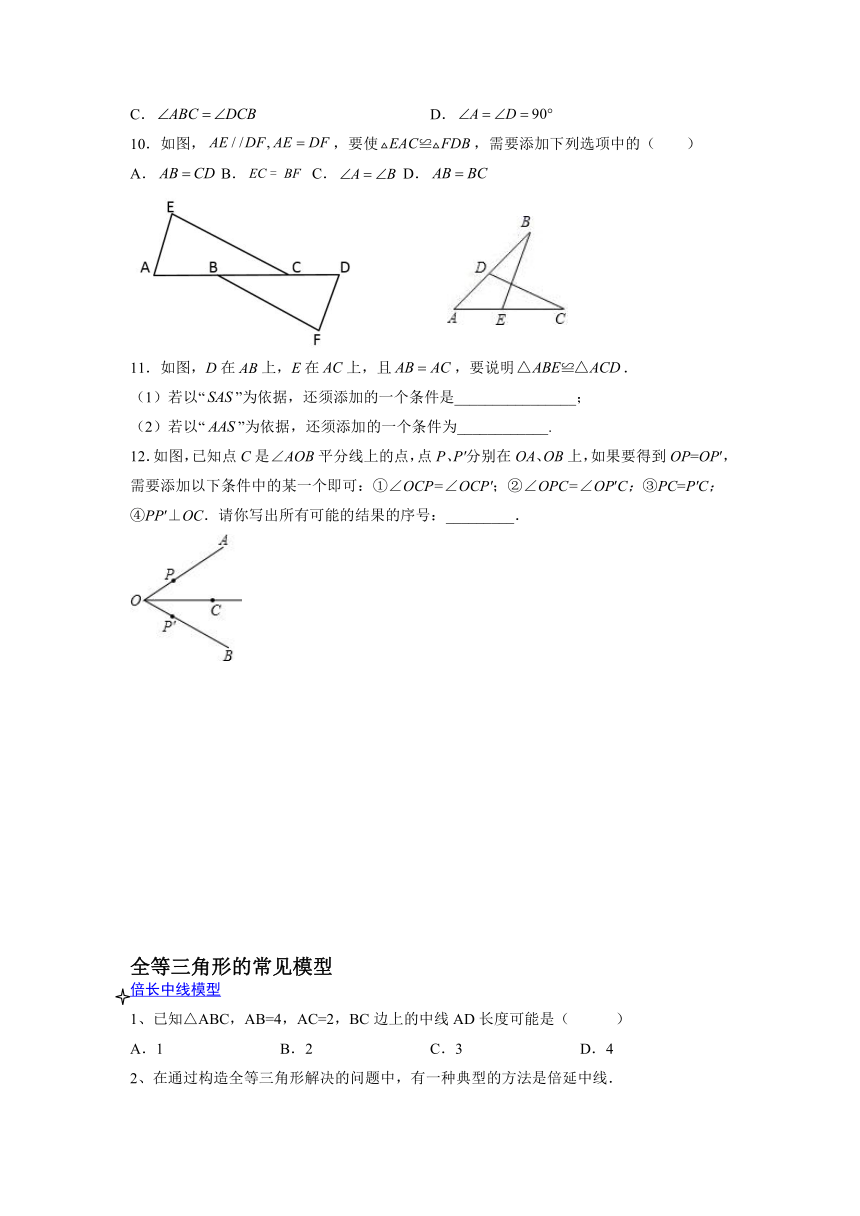
10.如图,,要使,需要添加下列选项中的( )
A. B. C. D.
11.如图,D在上,E在上,且,要说明.
(1)若以“”为依据,还须添加的一个条件是________________;
(2)若以“”为依据,还须添加的一个条件为____________.
12.如图,已知点C是∠AOB平分线上的点,点P、P′分别在OA、OB上,如果要得到OP=OP′,需要添加以下条件中的某一个即可:①∠OCP=∠OCP′;②∠OPC=∠OP′C;③PC=P′C;④PP′⊥OC.请你写出所有可能的结果的序号:_________.
全等三角形的常见模型
倍长中线模型
1、已知△ABC,AB=4,AC=2,BC边上的中线AD长度可能是( )
A.1 B.2 C.3 D.4
2、在通过构造全等三角形解决的问题中,有一种典型的方法是倍延中线.
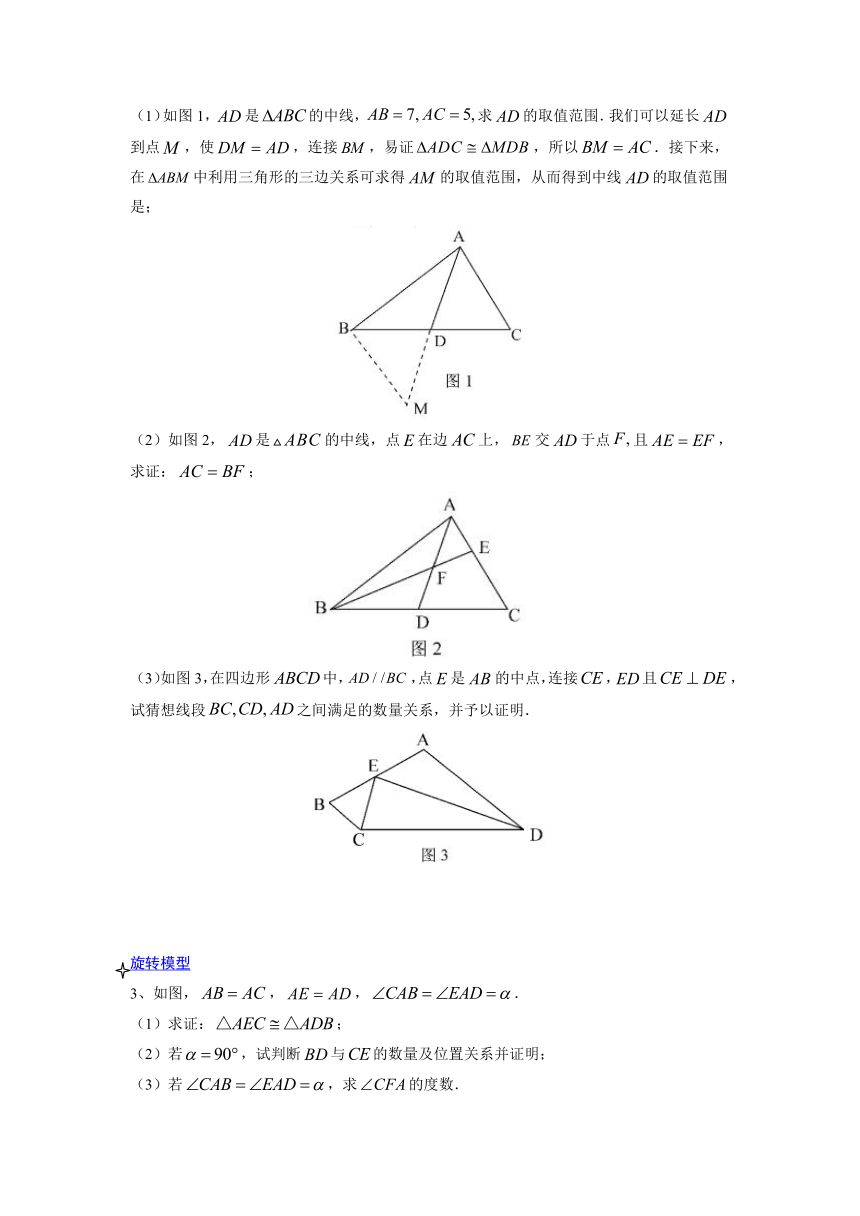
(1)如图1,是的中线,求的取值范围.我们可以延长到点,使,连接,易证,所以.接下来,在中利用三角形的三边关系可求得的取值范围,从而得到中线的取值范围是;
(2)如图2,是的中线,点在边上,交于点且,求证:;
(3)如图3,在四边形中,,点是的中点,连接,且,试猜想线段之间满足的数量关系,并予以证明.
旋转模型
3、如图,,,.
(1)求证:;
(2)若,试判断与的数量及位置关系并证明;
(3)若,求的度数.
一线三角模型
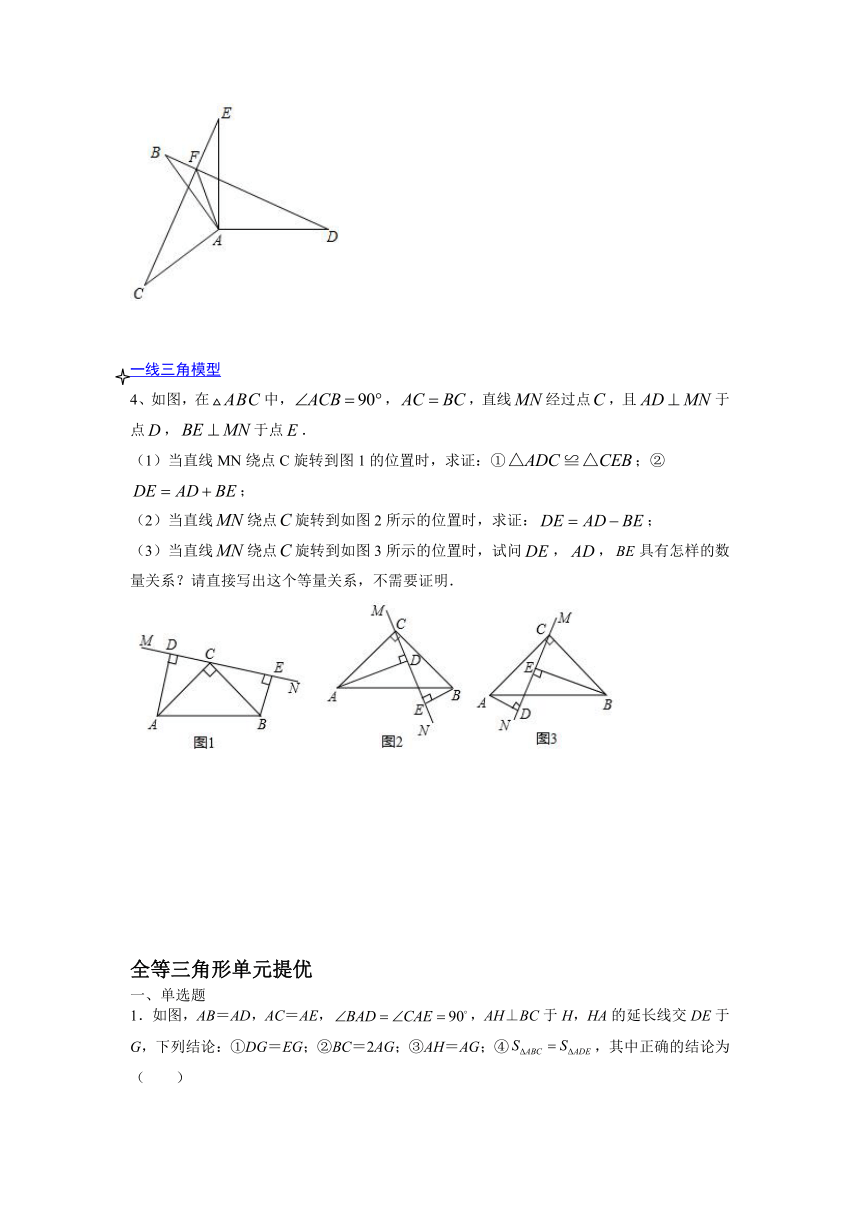
4、如图,在中,,,直线经过点,且于点,于点.
(1)当直线MN绕点C旋转到图1的位置时,求证:①;②;
(2)当直线绕点旋转到如图2所示的位置时,求证:;
(3)当直线绕点旋转到如图3所示的位置时,试问,,具有怎样的数量关系?请直接写出这个等量关系,不需要证明.
全等三角形单元提优
一、单选题
1.如图,AB=AD,AC=AE,,AH⊥BC于H,HA的延长线交DE于G,下列结论:①DG=EG;②BC=2AG;③AH=AG;④,其中正确的结论为( )
A.①②③ B.①②④ C.②③④ D.①②③④
2.如图,已知,点D、E分别在、上且,连接交于点M,连接,过点A分别作,垂足分别为F、G,下列结论:①;②;③平分;④如果,则E是的中点;其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
3.如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,AF是△ADC的中线,C,D,E三点在一条直线上,连接BD,BE,以下五个结论:①BD=CE:②BD⊥CE;③∠ACE+∠DBC=45°;④2AF=BE⑤BE⊥AF中正确的个数是( )
A.2 B.3 C.4 D.5
4.如图,Rt△ACB中,∠ACB=90°,△ACB的角平分线AD,BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°; ②AD=PF+PH;③DH平分∠CDE;④S四边形ABDE=S△ABP;⑤S△APH=S△ADE,其中正确的结论有( )个
A.2 B.3 C.4 D.5
5.如图,在△ABC中,∠ABC=90°,AB=BC,AE是中线,过点B作BF⊥AE于点F,过点C作CD⊥BC交BF的延长线于点D.下列结论:①BE=CE;②AE=BD;③∠BAE=∠CBD;④∠EAC=∠BAE;⑤BC=2CD.正确的个数是( )
A.2个 B.3个 C.4个 D.5个
6.如图,已知AB=AC,点D、E分别在AC、AB上且AE=AD,连接EC,BD,EC交BD于点M,连接AM,过点A分别做AF⊥CE,AG⊥BD垂足分别为F、G,下列结论:①△EBM≌△DCM;②∠EMB=∠FAG;③MA平分∠EMD;④若点E是AB的中点,则BM+AC>EM+BD;⑤如果S△BEM=S△ADM,则E是AB的中点;其中正确结论的个数为( )
A.2个 B.3个 C.4个 D.5个
二、填空题
7.如图,为等腰的高,其中分别为线段上的动点,且,当取最小值时,的度数为_____.
8.如图,在四边形ABCD中,AD=AB,DC=BC,∠DAB=60°,∠DCB=120°,E在AD上,F是AB延长线上一点,且DE=BF,若G在AB上,且∠ECG=60°,则DE、EG、BG之间的数量关系是_____.
9.如图,在中,和的平分线、相交于点,交于点,交于点,过点作于点,则下列三个结论:①;②当时,;③若,,则.其中正确的是______.
10.如图,在ABC中,AH是高,AEBC,AB=AE,在AB边上取点D,连接DE,DE=AC,若,BH=1,则BC=______.
11.如图,△ABC中,∠ACB= 90°,AC= 6,BC= 8,点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥于E,当点P运动 _________ 秒时,以P、E、C为顶点的三角形上以O、F、C为顶点的三角形全等.
12.如图,在中,,,、是斜边上两点,过点作,垂足是,过点作,垂足是.交于点,连接,其中.下列结论:①;②;③若,.则;④.其中正确的是__________.(填序号).
三、解答题
13.如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB,DE交于点F.
(1)试说明AB=DE,DE⊥AB.
(2)连接BD,BE,若设BC=a,AC=b,AB=c,请利用四边形ADBE的面积说明a2+b2=c2.
14.数学兴趣小组在活动时,老师提出了这样一个问题:
如图1,在中,,,D是BC的中点,求BC边上的中线AD的取值范围.
(阅读理解)
小明在组内经过合作交流,得到了如下的解决方法:
(1)如图1,延长AD到E点,使,连接BE.根据______可以判定 ______,得出______.这样就能把线段AB、AC、集中在中.利用三角形三边的关系,即可得出中线AD的取值范围是.
(方法感悟)
当条件中出现“中点”、“中线”等条件时,可以考虑做“辅助线”——把中线延长一倍,构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中,这种做辅助线的方法称为“中线加倍”法.
(问题解决)
(2)如图2,在中,,D是BC边的中点,,DE交AB于点E,DF交AC于点F,连接EF,求证:.
(问题拓展)
(3)如图3,中,,,AD是的中线,,,且.直接写出AE的长=______.
15.如图,点D是△ABC中∠BAC的平分线和边BC的垂直平分线DE的交点,DG⊥AB于点G,DH⊥AC交AC的延长线于点H.
(1)求证:BG=CH;
(2)若AB=12,AC=8,求BG的长.
16.如图1,在△ABC中,AE⊥BC于E,AE=BE,D是AE上一点,且DE=CE,连接BD,CD.
(1)判断与的位置关系和数量关系,并证明;
(2)如图2,若将△DCE绕点E旋转一定的角度后,BD与AC的位置关系和数量关系是否发生变化?并证明;
(3)如图3,将(2)中的等腰直角三角形都换成等边三角形,其他条件不变,求BD与AC夹角的度数.
全等三角形
全等三角形知识点提优
知识点一、全等三角形的概念与性质
1.如图,把沿线段折叠,使点落在点处;若,,,则的度数为( )
A. B. C. D.
2.如图ABC≌,边过点A且平分∠BAC交BC于点D,∠B=26°,=94°,则的度数为( )
A.34° B.40° C.45° D.60°
3.如图,在长方形ABCD中,,.延长BC到点E,使,连结DE,动点P从点B出发,以每秒2个单位长度的速度沿向终点A运动.设点P的运动时间为t秒,当t的值为____________时,和全等.
4.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,己知DE=4,AD=6,则BE的长为 ____________
知识点二、全等三角形的判定
5.如图,边长为a的等边△ABC中,BF是AC上中线且BF=b,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,则△AEF周长的最小值是( )
A. B. C.a+b D.a
6.如图,在△ABC中,∠BAC=120°,将△ABC绕点C逆时针旋转得到△DEC,点A,B的对应点分别为D,E,连接AD.当点A,D,E在同一条直线上时,给出下列4个结论①∠ABC=∠ADC;②CB=CD;③DE+DC=BC;④AB∥CD.一定正确的有( )个.
A.1 B.2 C.3 D.4
7.如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,连结BE、CD交于点F.将△ADC和△AEB分别绕着边AB、AC翻折得到△ADC'和△AEB',且EB'∥DC'∥BC,若∠BAC=42°,则∠BFC的大小是 ___.
8.如图,在直角坐标系中,已知A(4,0),点B为y轴正半轴上一动点,连接AB,以AB为一边向下做等边△ABC,连接OC,则OC的最小值为_______.
知识点三、补充条件型全等
9.如图,已知,添加下列条件,不能判定的是( )
A. B.
C. D.
10.如图,,要使,需要添加下列选项中的( )
A. B. C. D.
11.如图,D在上,E在上,且,要说明.
(1)若以“”为依据,还须添加的一个条件是________________;
(2)若以“”为依据,还须添加的一个条件为____________.
12.如图,已知点C是∠AOB平分线上的点,点P、P′分别在OA、OB上,如果要得到OP=OP′,需要添加以下条件中的某一个即可:①∠OCP=∠OCP′;②∠OPC=∠OP′C;③PC=P′C;④PP′⊥OC.请你写出所有可能的结果的序号:_________.
全等三角形的常见模型
倍长中线模型
1、已知△ABC,AB=4,AC=2,BC边上的中线AD长度可能是( )
A.1 B.2 C.3 D.4
2、在通过构造全等三角形解决的问题中,有一种典型的方法是倍延中线.
(1)如图1,是的中线,求的取值范围.我们可以延长到点,使,连接,易证,所以.接下来,在中利用三角形的三边关系可求得的取值范围,从而得到中线的取值范围是;
(2)如图2,是的中线,点在边上,交于点且,求证:;
(3)如图3,在四边形中,,点是的中点,连接,且,试猜想线段之间满足的数量关系,并予以证明.
旋转模型
3、如图,,,.
(1)求证:;
(2)若,试判断与的数量及位置关系并证明;
(3)若,求的度数.
一线三角模型
4、如图,在中,,,直线经过点,且于点,于点.
(1)当直线MN绕点C旋转到图1的位置时,求证:①;②;
(2)当直线绕点旋转到如图2所示的位置时,求证:;
(3)当直线绕点旋转到如图3所示的位置时,试问,,具有怎样的数量关系?请直接写出这个等量关系,不需要证明.
全等三角形单元提优
一、单选题
1.如图,AB=AD,AC=AE,,AH⊥BC于H,HA的延长线交DE于G,下列结论:①DG=EG;②BC=2AG;③AH=AG;④,其中正确的结论为( )
A.①②③ B.①②④ C.②③④ D.①②③④
2.如图,已知,点D、E分别在、上且,连接交于点M,连接,过点A分别作,垂足分别为F、G,下列结论:①;②;③平分;④如果,则E是的中点;其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
3.如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,AF是△ADC的中线,C,D,E三点在一条直线上,连接BD,BE,以下五个结论:①BD=CE:②BD⊥CE;③∠ACE+∠DBC=45°;④2AF=BE⑤BE⊥AF中正确的个数是( )
A.2 B.3 C.4 D.5
4.如图,Rt△ACB中,∠ACB=90°,△ACB的角平分线AD,BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°; ②AD=PF+PH;③DH平分∠CDE;④S四边形ABDE=S△ABP;⑤S△APH=S△ADE,其中正确的结论有( )个
A.2 B.3 C.4 D.5
5.如图,在△ABC中,∠ABC=90°,AB=BC,AE是中线,过点B作BF⊥AE于点F,过点C作CD⊥BC交BF的延长线于点D.下列结论:①BE=CE;②AE=BD;③∠BAE=∠CBD;④∠EAC=∠BAE;⑤BC=2CD.正确的个数是( )
A.2个 B.3个 C.4个 D.5个
6.如图,已知AB=AC,点D、E分别在AC、AB上且AE=AD,连接EC,BD,EC交BD于点M,连接AM,过点A分别做AF⊥CE,AG⊥BD垂足分别为F、G,下列结论:①△EBM≌△DCM;②∠EMB=∠FAG;③MA平分∠EMD;④若点E是AB的中点,则BM+AC>EM+BD;⑤如果S△BEM=S△ADM,则E是AB的中点;其中正确结论的个数为( )
A.2个 B.3个 C.4个 D.5个
二、填空题
7.如图,为等腰的高,其中分别为线段上的动点,且,当取最小值时,的度数为_____.
8.如图,在四边形ABCD中,AD=AB,DC=BC,∠DAB=60°,∠DCB=120°,E在AD上,F是AB延长线上一点,且DE=BF,若G在AB上,且∠ECG=60°,则DE、EG、BG之间的数量关系是_____.
9.如图,在中,和的平分线、相交于点,交于点,交于点,过点作于点,则下列三个结论:①;②当时,;③若,,则.其中正确的是______.
10.如图,在ABC中,AH是高,AEBC,AB=AE,在AB边上取点D,连接DE,DE=AC,若,BH=1,则BC=______.
11.如图,△ABC中,∠ACB= 90°,AC= 6,BC= 8,点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥于E,当点P运动 _________ 秒时,以P、E、C为顶点的三角形上以O、F、C为顶点的三角形全等.
12.如图,在中,,,、是斜边上两点,过点作,垂足是,过点作,垂足是.交于点,连接,其中.下列结论:①;②;③若,.则;④.其中正确的是__________.(填序号).
三、解答题
13.如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB,DE交于点F.
(1)试说明AB=DE,DE⊥AB.
(2)连接BD,BE,若设BC=a,AC=b,AB=c,请利用四边形ADBE的面积说明a2+b2=c2.
14.数学兴趣小组在活动时,老师提出了这样一个问题:
如图1,在中,,,D是BC的中点,求BC边上的中线AD的取值范围.
(阅读理解)
小明在组内经过合作交流,得到了如下的解决方法:
(1)如图1,延长AD到E点,使,连接BE.根据______可以判定 ______,得出______.这样就能把线段AB、AC、集中在中.利用三角形三边的关系,即可得出中线AD的取值范围是.
(方法感悟)
当条件中出现“中点”、“中线”等条件时,可以考虑做“辅助线”——把中线延长一倍,构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中,这种做辅助线的方法称为“中线加倍”法.
(问题解决)
(2)如图2,在中,,D是BC边的中点,,DE交AB于点E,DF交AC于点F,连接EF,求证:.
(问题拓展)
(3)如图3,中,,,AD是的中线,,,且.直接写出AE的长=______.
15.如图,点D是△ABC中∠BAC的平分线和边BC的垂直平分线DE的交点,DG⊥AB于点G,DH⊥AC交AC的延长线于点H.
(1)求证:BG=CH;
(2)若AB=12,AC=8,求BG的长.
16.如图1,在△ABC中,AE⊥BC于E,AE=BE,D是AE上一点,且DE=CE,连接BD,CD.
(1)判断与的位置关系和数量关系,并证明;
(2)如图2,若将△DCE绕点E旋转一定的角度后,BD与AC的位置关系和数量关系是否发生变化?并证明;
(3)如图3,将(2)中的等腰直角三角形都换成等边三角形,其他条件不变,求BD与AC夹角的度数.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
