北京版八年级数学上册《12.11 勾股定理》教学设计
文档属性
| 名称 | 北京版八年级数学上册《12.11 勾股定理》教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 378.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 00:00:00 | ||
图片预览

文档简介
勾股定理
一、教材分析
勾股定理是初中数学中一个非常重要的结论,称为“几何学的基石”,在数学学习中有重要的地位。本定理揭示的是直角三角形三边的数量关系,在此之前学生对直角三角形已有了初步认识,但是都停留在直观感知方面。后面直角三角形的相似和全等、锐角三角函数、解直角三角形的学习都与此密切相关。
学生分析:八年级的学生已经具备一定的几何证明基础,但是思维偏重于直观。而勾股定理的证明是先构造图形,数形结合,再进行证明。与以往的几何题目证明相差甚远,有很大的难度。由此本课的设计注重从学生的动手操作开始,从特殊到一般,层层递进,引导学生亲历定理的产生和证明过程,且能初步运用,为以后相关知识的继续学习奠定良好的基础。
二、教学目标及重难点:
(一)教学目标
1、认知目标:理解并掌握勾股定理的证明;并且能初步运用勾股定理解决问题。
2、技能目标:在探索过程中,让学生亲历“观察—猜想—归纳—证明”的过程,并且能体会特殊到一般、数形结合的数学思想和方法。
序号 媒体内容 媒体作用 使用时间
1 电视机尺寸大小 创设情境,导入新课 1分钟
2 活动1:数学家从地板找灵感 探究等腰三角形两直角边和斜边的关系 3分钟
3 活动2: 探究一般三角形两直角边和斜边的关系 3分钟
4 赵爽勾股圆方图 证明勾股定理 2分钟
5 毕达哥拉斯证法 证明勾股定理 2分钟
6 总统证法 证明勾股定理 2分钟
7 勾股定理应用方法 方法归纳 2分钟
8 选一选 巩固新知 1分钟
9 讲一讲 应用新知 2分钟
10 做一做 运用新知 1.5分钟
11 用一用 解决问题 2分钟
12 回头看一看 解决课前问题 2分钟
13 课堂小结 应用新知,反馈矫正 2分钟
情感目标:通过了解与定理有关的中外数学史,激发学生的学习兴趣和研究精神。特别是通过了解中国古代的数学成就,激发学生的民族自豪感。
(二)教学重点:勾股定理的证明和运用
(三)教学难点:勾股定理的证明
教学过程
(一)创设情境,导入新课
问题: 国庆节前,为了更好观看阅兵式,小明妈妈买了一部42英寸(106厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有85厘米长和64厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
画出图形后,指出需要解决的问题“已知直角三角形的两边,怎样求第三边?”通过本节的学习我们可以解决这个问题。
(二)合作交流,探究新知
早在2500年前,古希腊数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了灵感,并且对此展开研究,下面我们也来重温数学家的发现之路,探究这个“饭局中诞生的定理”。
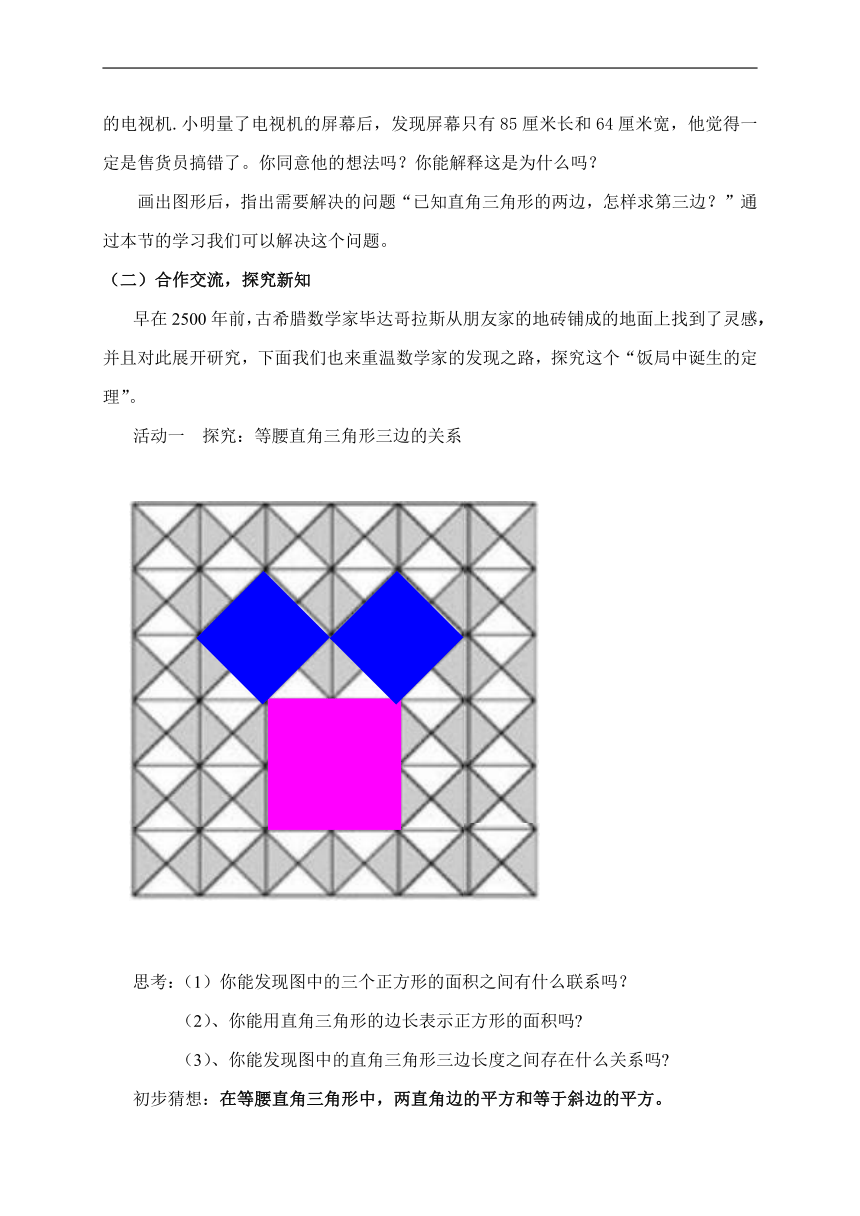
活动一 探究:等腰直角三角形三边的关系
思考:(1)你能发现图中的三个正方形的面积之间有什么联系吗?
(2)、你能用直角三角形的边长表示正方形的面积吗
(3)、你能发现图中的直角三角形三边长度之间存在什么关系吗
初步猜想:在等腰直角三角形中,两直角边的平方和等于斜边的平方。
活动二 探究:一般直角三角形三边之间的关系是否也是如此?
(1)图形A的面积= ,图形B的面积=
交流:图形C的面积如何求出?
(2)、你能用直角三角形的边长表示正方形的面积吗
(3)、你能发现图中的直角三角形三边长度之间存在什么关系吗
进一步猜想:在直角三角形中,两直角边的平方和等于斜边的平方。
以上仅仅是我们的猜想,这个命题如何来进行证明呢?
(三)动手操作,证明结论
我国古代人民早在几千万年以前就已经发现和运用勾股定理,在已有的文献记载中,最早给出证明的是三国时期的吴国数学家赵爽在《周髀算经》注中已经给出了勾股定理的证明。指导学生利用手中4个全等的直角三角形进行拼图。
1. 赵爽“勾股圆方图”
大正方形的面积可以表示为
也可以表示为4×+,于是可得:=4×+
整理的:
得到勾股定理在直角三角形中,两直角边的平方和等于斜边的平方。
2、传说中的毕达哥拉斯证法
由于拼图前后面积没有发生变化,因此
S大正方形==
S大正方形==
所以:= 得到:
3.总统证法(自主完成)
(四)应用新知,反馈矫正
1.讲一讲
求图中直角三角形的未知边的长度
2.做一做
在Rt△ABC中,∠C=900
(1)若a=5,b=12, 则c =___________.
(2)若c=4,b= 2 ,则a =______.
3.用一用
如图,受台风影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4.回头再看看
国庆节前,为了更好观看阅兵式,小明妈妈买了一部42英寸(106厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有85厘米长和64厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
(五)师生小结、共同提升
通过本节的学习,你有什么收获?(知识、过程、情感)还有什么困惑?
五、教学反思
本节课从实际问题引入,激发学生的学习兴趣。数学家毕达哥拉斯的发现之路也体现了数学来源于生活,又服务于生活,激发学生的研究热情。然后整个教学流程从特殊的等腰直角三角形到一般的直角三角形,从最初的猜想到最后的证明,既体现了数学的严谨,又符合学生的认知特点,便于学生接受和理解。其中勾股定理的证明方法多样化,利用数形结合,给出严密的证明。在给出证明方法的同时对学生进行数学史教育,中外都有所涉及,特别是通过中国古代对勾股定理的证明和利用,激发民族自豪感和爱国热忱。
六、教学流程图
一、教材分析
勾股定理是初中数学中一个非常重要的结论,称为“几何学的基石”,在数学学习中有重要的地位。本定理揭示的是直角三角形三边的数量关系,在此之前学生对直角三角形已有了初步认识,但是都停留在直观感知方面。后面直角三角形的相似和全等、锐角三角函数、解直角三角形的学习都与此密切相关。
学生分析:八年级的学生已经具备一定的几何证明基础,但是思维偏重于直观。而勾股定理的证明是先构造图形,数形结合,再进行证明。与以往的几何题目证明相差甚远,有很大的难度。由此本课的设计注重从学生的动手操作开始,从特殊到一般,层层递进,引导学生亲历定理的产生和证明过程,且能初步运用,为以后相关知识的继续学习奠定良好的基础。
二、教学目标及重难点:
(一)教学目标
1、认知目标:理解并掌握勾股定理的证明;并且能初步运用勾股定理解决问题。
2、技能目标:在探索过程中,让学生亲历“观察—猜想—归纳—证明”的过程,并且能体会特殊到一般、数形结合的数学思想和方法。
序号 媒体内容 媒体作用 使用时间
1 电视机尺寸大小 创设情境,导入新课 1分钟
2 活动1:数学家从地板找灵感 探究等腰三角形两直角边和斜边的关系 3分钟
3 活动2: 探究一般三角形两直角边和斜边的关系 3分钟
4 赵爽勾股圆方图 证明勾股定理 2分钟
5 毕达哥拉斯证法 证明勾股定理 2分钟
6 总统证法 证明勾股定理 2分钟
7 勾股定理应用方法 方法归纳 2分钟
8 选一选 巩固新知 1分钟
9 讲一讲 应用新知 2分钟
10 做一做 运用新知 1.5分钟
11 用一用 解决问题 2分钟
12 回头看一看 解决课前问题 2分钟
13 课堂小结 应用新知,反馈矫正 2分钟
情感目标:通过了解与定理有关的中外数学史,激发学生的学习兴趣和研究精神。特别是通过了解中国古代的数学成就,激发学生的民族自豪感。
(二)教学重点:勾股定理的证明和运用
(三)教学难点:勾股定理的证明
教学过程
(一)创设情境,导入新课
问题: 国庆节前,为了更好观看阅兵式,小明妈妈买了一部42英寸(106厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有85厘米长和64厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
画出图形后,指出需要解决的问题“已知直角三角形的两边,怎样求第三边?”通过本节的学习我们可以解决这个问题。
(二)合作交流,探究新知
早在2500年前,古希腊数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了灵感,并且对此展开研究,下面我们也来重温数学家的发现之路,探究这个“饭局中诞生的定理”。
活动一 探究:等腰直角三角形三边的关系
思考:(1)你能发现图中的三个正方形的面积之间有什么联系吗?
(2)、你能用直角三角形的边长表示正方形的面积吗
(3)、你能发现图中的直角三角形三边长度之间存在什么关系吗
初步猜想:在等腰直角三角形中,两直角边的平方和等于斜边的平方。
活动二 探究:一般直角三角形三边之间的关系是否也是如此?
(1)图形A的面积= ,图形B的面积=
交流:图形C的面积如何求出?
(2)、你能用直角三角形的边长表示正方形的面积吗
(3)、你能发现图中的直角三角形三边长度之间存在什么关系吗
进一步猜想:在直角三角形中,两直角边的平方和等于斜边的平方。
以上仅仅是我们的猜想,这个命题如何来进行证明呢?
(三)动手操作,证明结论
我国古代人民早在几千万年以前就已经发现和运用勾股定理,在已有的文献记载中,最早给出证明的是三国时期的吴国数学家赵爽在《周髀算经》注中已经给出了勾股定理的证明。指导学生利用手中4个全等的直角三角形进行拼图。
1. 赵爽“勾股圆方图”
大正方形的面积可以表示为
也可以表示为4×+,于是可得:=4×+
整理的:
得到勾股定理在直角三角形中,两直角边的平方和等于斜边的平方。
2、传说中的毕达哥拉斯证法
由于拼图前后面积没有发生变化,因此
S大正方形==
S大正方形==
所以:= 得到:
3.总统证法(自主完成)
(四)应用新知,反馈矫正
1.讲一讲
求图中直角三角形的未知边的长度
2.做一做
在Rt△ABC中,∠C=900
(1)若a=5,b=12, 则c =___________.
(2)若c=4,b= 2 ,则a =______.
3.用一用
如图,受台风影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4.回头再看看
国庆节前,为了更好观看阅兵式,小明妈妈买了一部42英寸(106厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有85厘米长和64厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
(五)师生小结、共同提升
通过本节的学习,你有什么收获?(知识、过程、情感)还有什么困惑?
五、教学反思
本节课从实际问题引入,激发学生的学习兴趣。数学家毕达哥拉斯的发现之路也体现了数学来源于生活,又服务于生活,激发学生的研究热情。然后整个教学流程从特殊的等腰直角三角形到一般的直角三角形,从最初的猜想到最后的证明,既体现了数学的严谨,又符合学生的认知特点,便于学生接受和理解。其中勾股定理的证明方法多样化,利用数形结合,给出严密的证明。在给出证明方法的同时对学生进行数学史教育,中外都有所涉及,特别是通过中国古代对勾股定理的证明和利用,激发民族自豪感和爱国热忱。
六、教学流程图
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
