勾股定理学案
图片预览
文档简介
人教版八年级数学下18.1勾股定理(1)导学案
学科:数学 设计人:79团子校车鸣丽 使用时间:2013.3 班级: 姓名:
【学习目标】1、了解勾股定理的由来,经历探索勾股定理的过程,理解并能用面积法证明勾股定理,并能简单的运用。
2、提高推理意识与探究习惯,感受我国古代数学的伟大成就。
【重点难点】学习重点:探索和证明勾股定理。
学习难点:用面积法(拼图法)证明勾股定理.
【学前准备】1、每位同学准备四个全等的直角三角形。
2、查阅资料,网络搜索有关勾股定理的知识。
3、自主阅读课本本节内容。
【学习过程】:
一、提出问题:
在直角三角形中,已知两直角边的长度,用已学知识能求出第三边的长度吗?
二、了解勾股定理的文化背景。
三、探究问题:
(一)探究1:等腰直角三角形:
下图中,每个小方格的面积均为1,请分别计算出下图中正方形P、Q、R的面积,看看能得出什么结论.
(1)发现:正方形_______的面积+正方形________的面积=正方形________的面积;
(2)你能用三角形ABC的边长表示正方形的面积吗?你能发现等腰直角三角形ABC三边长度之间存在什么关系吗?
(3)归纳:在等腰直角三角形中:两直角边的_______等于斜边的________。
(二)探究2:任意直角三角形:
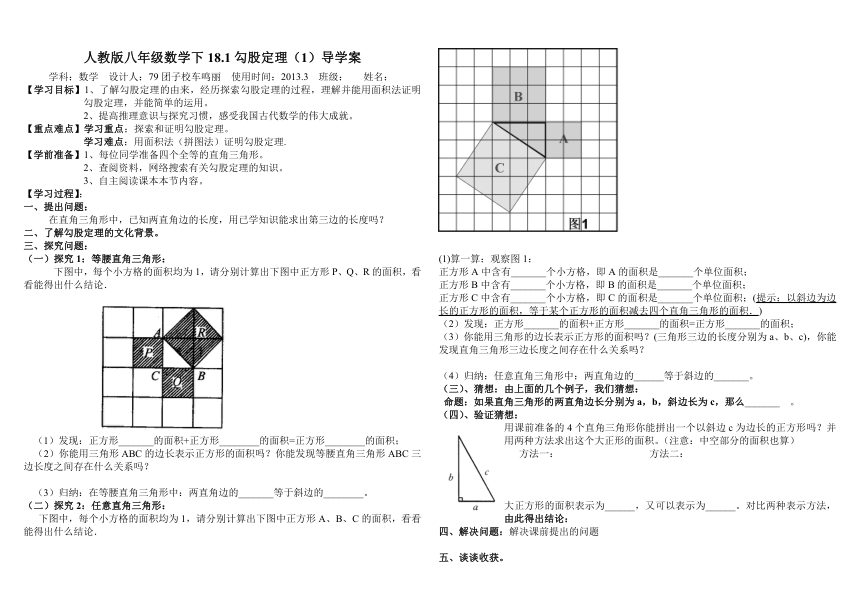
下图中,每个小方格的面积均为1,请分别计算出下图中正方形A、B、C的面积,看看能得出什么结论.
(1)算一算:观察图1:
正方形A中含有_______个小方格,即A的面积是_______个单位面积;
正方形B中含有_______个小方格,即B的面积是_______个单位面积;
正方形C中含有_______个小方格,即C的面积是_______个单位面积;(提示:以斜边为边长的正方形的面积,等于某个正方形的面积减去四个直角三角形的面积.)
(2)发现:正方形_______的面积+正方形_______的面积=正方形_______的面积;
(3)你能用三角形的边长表示正方形的面积吗?(三角形三边的长度分别为a、b、c),你能发现直角三角形三边长度之间存在什么关系吗?
(4)归纳:任意直角三角形中:两直角边的______等于斜边的_______。
(三)、猜想:由上面的几个例子,我们猜想:
命题:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么_______ 。
(四)、验证猜想:
用课前准备的4个直角三角形你能拼出一个以斜边c为边长的正方形吗?并用两种方法求出这个大正形的面积。(注意:中空部分的面积也算)
方法一: 方法二:
大正方形的面积表示为______,又可以表示为______。对比两种表示方法,由此得出结论:
四、解决问题:解决课前提出的问题
五、谈谈收获。
勾股定理达标检测
姓名: 得分:
1、求下图中字母所代表的数值。(每题30分,共60分)
(1) (2)
正方形A的面积为_______ 直角三角形的斜边x长为_______
2、求出下列直角三角形中未知的边:(40分)
勾股定理达标检测
姓名: 得分:
1、求下图中字母所代表的数值。(每题30分,共60分)
(1) (2)
正方形A的面积为_______ 直角三角形的斜边x长为_______
2、求出下列直角三角形中未知的边: (40分)
勾股定理达标检测
姓名: 得分:
1、求下图中字母所代表的数值。(每题30分,共60分)
(1) (2)
正方形A的面积为_______ 直角三角形的斜边x长为_______
2、求出下列直角三角形中未知的边: (40分)
勾股定理达标检测
姓名: 得分:
1、求下图中字母所代表的数值。(每题30分,共60分)
(1) (2)
正方形A的面积为_______ 直角三角形的斜边x长为_______
2、求出下列直角三角形中未知的边: (40分)
学科:数学 设计人:79团子校车鸣丽 使用时间:2013.3 班级: 姓名:
【学习目标】1、了解勾股定理的由来,经历探索勾股定理的过程,理解并能用面积法证明勾股定理,并能简单的运用。
2、提高推理意识与探究习惯,感受我国古代数学的伟大成就。
【重点难点】学习重点:探索和证明勾股定理。
学习难点:用面积法(拼图法)证明勾股定理.
【学前准备】1、每位同学准备四个全等的直角三角形。
2、查阅资料,网络搜索有关勾股定理的知识。
3、自主阅读课本本节内容。
【学习过程】:
一、提出问题:
在直角三角形中,已知两直角边的长度,用已学知识能求出第三边的长度吗?
二、了解勾股定理的文化背景。
三、探究问题:
(一)探究1:等腰直角三角形:
下图中,每个小方格的面积均为1,请分别计算出下图中正方形P、Q、R的面积,看看能得出什么结论.
(1)发现:正方形_______的面积+正方形________的面积=正方形________的面积;
(2)你能用三角形ABC的边长表示正方形的面积吗?你能发现等腰直角三角形ABC三边长度之间存在什么关系吗?
(3)归纳:在等腰直角三角形中:两直角边的_______等于斜边的________。
(二)探究2:任意直角三角形:
下图中,每个小方格的面积均为1,请分别计算出下图中正方形A、B、C的面积,看看能得出什么结论.
(1)算一算:观察图1:
正方形A中含有_______个小方格,即A的面积是_______个单位面积;
正方形B中含有_______个小方格,即B的面积是_______个单位面积;
正方形C中含有_______个小方格,即C的面积是_______个单位面积;(提示:以斜边为边长的正方形的面积,等于某个正方形的面积减去四个直角三角形的面积.)
(2)发现:正方形_______的面积+正方形_______的面积=正方形_______的面积;
(3)你能用三角形的边长表示正方形的面积吗?(三角形三边的长度分别为a、b、c),你能发现直角三角形三边长度之间存在什么关系吗?
(4)归纳:任意直角三角形中:两直角边的______等于斜边的_______。
(三)、猜想:由上面的几个例子,我们猜想:
命题:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么_______ 。
(四)、验证猜想:
用课前准备的4个直角三角形你能拼出一个以斜边c为边长的正方形吗?并用两种方法求出这个大正形的面积。(注意:中空部分的面积也算)
方法一: 方法二:
大正方形的面积表示为______,又可以表示为______。对比两种表示方法,由此得出结论:
四、解决问题:解决课前提出的问题
五、谈谈收获。
勾股定理达标检测
姓名: 得分:
1、求下图中字母所代表的数值。(每题30分,共60分)
(1) (2)
正方形A的面积为_______ 直角三角形的斜边x长为_______
2、求出下列直角三角形中未知的边:(40分)
勾股定理达标检测
姓名: 得分:
1、求下图中字母所代表的数值。(每题30分,共60分)
(1) (2)
正方形A的面积为_______ 直角三角形的斜边x长为_______
2、求出下列直角三角形中未知的边: (40分)
勾股定理达标检测
姓名: 得分:
1、求下图中字母所代表的数值。(每题30分,共60分)
(1) (2)
正方形A的面积为_______ 直角三角形的斜边x长为_______
2、求出下列直角三角形中未知的边: (40分)
勾股定理达标检测
姓名: 得分:
1、求下图中字母所代表的数值。(每题30分,共60分)
(1) (2)
正方形A的面积为_______ 直角三角形的斜边x长为_______
2、求出下列直角三角形中未知的边: (40分)
