6.2 平行四边形的判定 课件(共39张PPT)
文档属性
| 名称 | 6.2 平行四边形的判定 课件(共39张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 972.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 11:00:06 | ||
图片预览









文档简介
(共39张PPT)
6.2 平行四边形的判定
北师大版八年级下册数学
第六章平行四边形
学行四边形之后,小明回家用细木棒钉制了一个平行四边形.第二天,小明拿着自己动手做的平行四边形向同学们展示.
小辉却问:你凭什么确定这四边形就是平行四边形呢
大家都困惑了……
情景引入
活动1:用两根长30cm的木条和两根长20cm的木条作为四边形的四条边,能否拼成一个平行四边形?与同伴进行交流.
20cm
30cm
猜测:两组对边分别相等的四边形是平行四边形.
一、平行四边形的判定定理1
合作探究
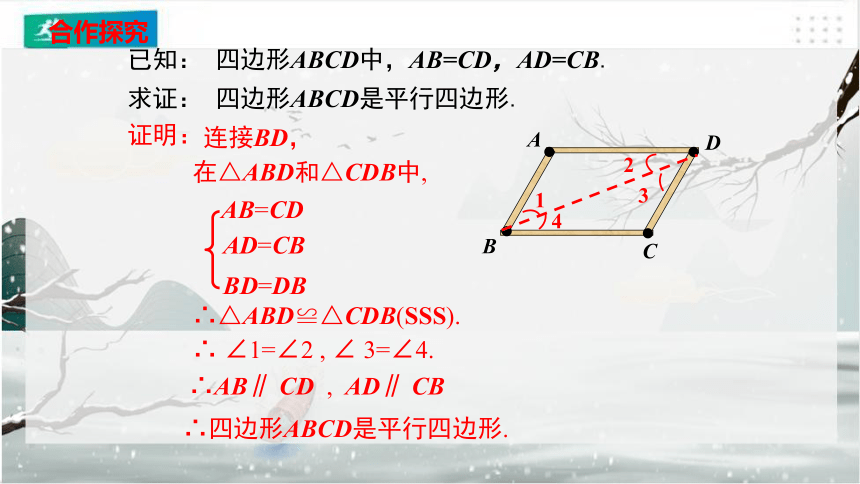
已知: 四边形ABCD中,AB=CD,AD=CB.
求证: 四边形ABCD是平行四边形.
A
B
C
D
连接BD,
在△ABD和△CDB中,
AB=CD
BD=DB
AD=CB
∴△ABD≌△CDB(SSS).
∴ ∠1=∠2 , ∠ 3=∠4.
∴AB∥ CD , AD∥ CB
∴四边形ABCD是平行四边形.
证明:
1
4
2
3
合作探究
两组对边分别相等的四边形是平行四边形.
∵AB=CD,
AD=BC
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理1
B
D
C
A
总结归纳
例1 如图,在平行四边形ABCD中,E、F分别是边BC和AD上的两点,且AF=CE.
求证:四边形AECF为平行四边形
B
A
C
D
F
E
证明:可求得△ABE≌△CDF(SAS)
∴AE=CF
又∵AF=CE
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
典例精析
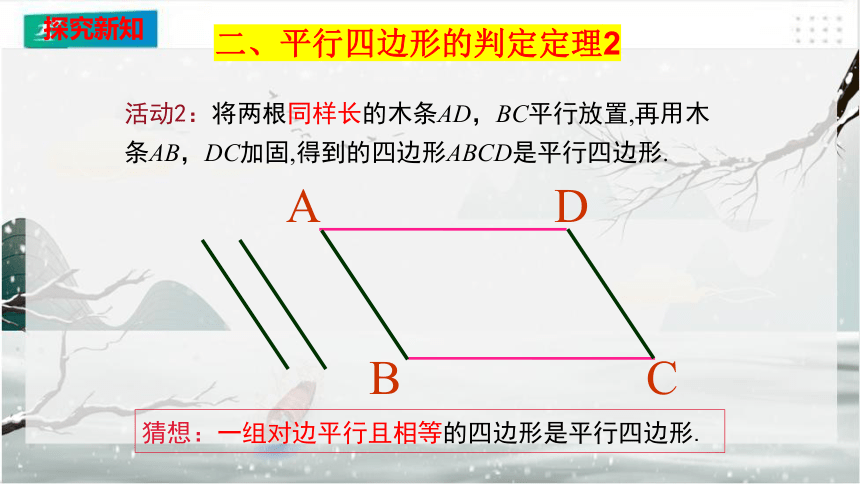
活动2:将两根同样长的木条AD,BC平行放置,再用木条AB,DC加固,得到的四边形ABCD是平行四边形.
A
B
C
D
猜想:一组对边平行且相等的四边形是平行四边形.
二、平行四边形的判定定理2
探究新知
连接AC.
∵AB//CD, ∴∠1=∠2.
又AB=CD,AC=CA,
∴△ABC≌△CDA(SAS).
∴BC=DA.
∴四边形ABCD的两组对边分别相等,它是平行四边形.
D
A
B
C
已知:如图,在四边形ABCD中,AB//CD.
求证:四边形ABCD是平行四边形.
证明:
1
2
探究新知
一组对边平行且相等的四边形是平行四边形.
∵AB=CD,
AB∥CD
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理2
B
D
C
A
总结归纳
例2 如图,在平行四边形ABCD中,已知AE、CF分别是∠DAB、∠BCD的角平分线,试证明四边形AFCE是平行四边形.
证明:∵在平行四边形ABCD中,
AE、CF分别是∠DAB、 ∠BCD的角平分线
∴∠B=∠D,AB=CD, AD∥BC
∠BAE=∠DCF= ∠DAB= ∠BCD
∴△ABE≌△CDF(ASA)
∴BE=DF∴AF=CE ∵AF∥CE
∴四边形AFCE是平行四边形(一组对边平行且相等的四边形是平行四边形)
例题讲解
卢师傅要做一个平行四边形木框.他要从图中几根木条中选出四根来制作,可是他不知道该怎样选,请同学们帮他选一选,哪四根木条可以制作成平行四边形木框,为什么?
7cm
4cm
3cm
3cm
5cm
4cm
阅读思考
4cm
4cm
4cm
4cm
3cm
3cm
3cm
3cm
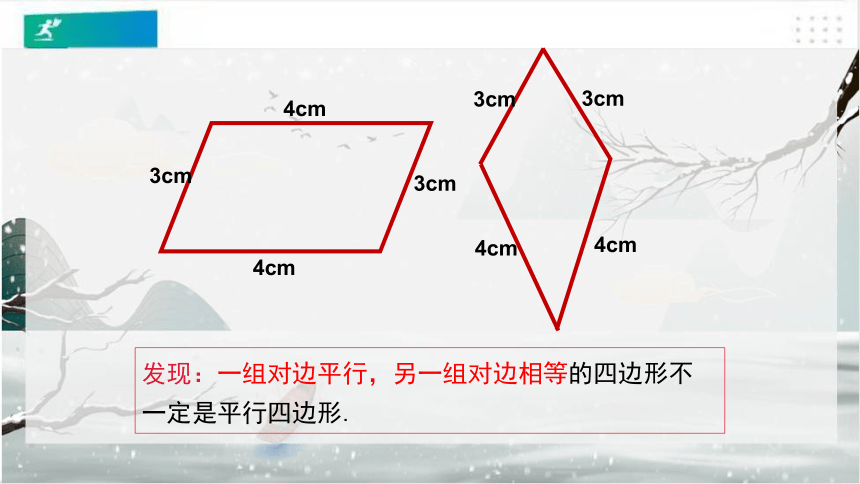
发现:一组对边平行,另一组对边相等的四边形不一定是平行四边形.
活动:
有一名同学将两根木条的中点重叠,并用钉子固定,得到如图的四边形,你认为这个四边形是平行四边形吗?
活动探究:做一做 :小组活动,回答下列问题。(小组讨论,3min)
三、平行四边形的判定定理3
探究新知
现在将你手中两根长度不等的细木条摆放在一张纸上,能否使得这两根细木条的四个端点恰好是一个平行四边形的四个顶点呢 做一做,与同伴交流.
活动探究:做一做 :小组活动,回答下列问题。(小组讨论,3min)
探究新知
已知:如图6-12,四边形ABCD的对角线AC、BD相交于点O,并且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
探究新知
证明: ∵ OA=OC,OD=OB,
∠AOD=∠COB,
∴ △AOD≌△COB.
∴ AD=CB,∠ADO=∠CBO,
∵ ∠ADO=∠CBO
∴ AD∥CB
∵ AD=CB且AD∥CB
∴ 四边形ABCD是平行四边形.
(一组对边平行且相等的四边形是平行四边形)
探究新知
思考:以上活动事实,能用文字语言表达吗?
平行四边形判定定理3:
对角线互相平分的四边形是平行四边形。
以上定理转换成数学语言是
如图
∵ OA=OC,OB=OD
∴ 四边形ABCD是平行四边形.
探究新知
例2:已知,如图6-13(1),在平行四边形ABCD中,
点E、F在对角线AC上,并且AE=CF.
求证:四边形BFDE是平行四边形吗?
证明: 如图,连接BD,交AC于点O.
∵ 四边形ABCD是平行四边形
∴ OA=OC,OB=OD.
又∵AE=CF
∴OA-AE=OC-CF,即OE=OF.
∴四边形BFDE是平行四边形.
(对角线互相平分的四边形是平行四边形)
探究新知
如图,在平行四边形ABCD中,对角线AC与BD相交于点O,E、F分别是OA和OC的中点,四边形BFDE是平行四边形吗?请说明理由。
探究新知
证明:∵四边形ABCD是平行四边形
∴OD=OB,OA=OC
∵E、F分别是AO、CO的中点
∴OE= OA,OF= OC
∴OE=OF
∴四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形)
2
1
2
1
探究新知
变式2:若E、F移至OA、OC的延长线上,且AE=CF,结论有改变吗?为什么?
探究新知
证明:∵四边形ABCD是平行四边形
∴OD=OB,OA=OC
∵ AE=CF
∴OE=OA+AE,OF=OC+CF
∴OE=OF
∴四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形)
探究新知
思考:我们可以从角出发来判定一个四边形是否为平行四边形吗?
A
B
C
D
你能根据平行四边形的定义证明它们吗?
四、由定义判定平行四边形
探究新知
已知:四边形ABCD中,∠A=∠C,∠B=∠D,
求证:四边形ABCD是平行四边形.
A
B
C
D
又∵∠A=∠C,∠B=∠D
∵∠A+∠C+∠B+∠D=360°
∴2∠A+2∠B=360°
即∠A+∠B=180°
∴ AD∥BC
∴四边形ABCD是平行四边形.
同理得 AB∥ CD
证明:
定义判定:
两组对角分别相等的四边形是平行四边形
探究新知
归纳小结
判定
定理1
定理2
定义判定
文字语言
图形语言
符号语言
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
平行四边形判定定理
A
B
C
D
∵AB=CD,AD=BC,
∴四边形ABCD是
ABCD
A
B
C
D
∵ AB= CD,
AB∥CD,
∴四边形ABCD是
ABCD
A
B
C
D
O
∵ ∠ A= ∠ C,
∠ B= ∠ D,
∴四边形ABCD是
ABCD
如图,在方格纸上画两条互相平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线,用刻度尺度量出平行线之间的垂线段的长度.
经过度量,我们发现这些垂线段的长度都相等(从图中也可以看到这一点).
猜想:平行线间距离处处相等.
活动:
平行线之间的距离
五、平行线之间的距离
探究新知
如图,直线a//b,A,B是直线a上任意两点,AC⊥b,BD⊥b,垂足分别为C,D.求证:AC=BD.
证明:∵AC⊥CD,BD⊥CD,
∴∠1=∠2=90°.
∴AC∥BD.
∵ AB∥CD,
∴四边形ACDB是平行四边形.
∴AC=BD.
a
b
A
B
C
D
1
2
猜想证明:
探究新知
如果两条直线互相平行,则其中一条直线上任意一点到另一条直线的距离都相等(如图:AC=BD),这个距离称为平行线之间的距离.
(简记为:两条平行线间的距离处处相等).
结论
探究新知
A
B
思考:两条平行线之间的距离与点和点之间的距离、点到线之间的距离有何区别与联系?
a
b
A
B
点到直线的距离只有一条,即过直线外一点作直线的垂线段的长度;而平行线的距离有无数条即一直线上任一点都可以得到一条两平行直线的距离.
结论
A
B
探究新知
思考:若垂线段改为夹在两条平行线间的平行线段呢?它们是否相等呢?
由“两组对边分别平行的四边形是平行四边形”易知其围成的封闭图形为平行四边形,再由平行四边形性质易知夹在两条平行线间的平行线段相等.
结论
探究新知
例 如图,甲船从北岸码头A向南行驶,航速为36千米/时;乙船从南岸码头B向北行驶,航速为27千米/时.两船均于7:15出发,两岸平行,水面宽为18.9千米,求两船距离最近时的时刻.
平行线之间的距离
例题讲解
解:设x分钟后两船距离最近,
当如图EF⊥BD,AE = DF时,两船距离最近,
根据题意得出:36x=18.9-27x, 解得x=0.3,
0.3小时=0.3×60分钟=18(分钟),
则两船距离最近时的时刻为7:33.
例题讲解
方法总结
平行线之间的距离概念辨析
注意:平行线之间的距离是指其中一条直线上的点到另一条直线的距离,是垂线段的长度,而不是垂线段.
作法:从其中一条直线上任意找一点,向另一条直线作垂线,垂线段的长度即平行线之间的距离.
如图,直线AE//BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为 .
A
B
C
D
E
分析:根据平行线之间的距离处处相等.
解析:设高为h,则S△ABD= ·BD·h=16,所以h=4,
所以S △ACE= ·AE·h= ×5 ×4=10.
10
变式训练
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD EF,EF BC.
∴AD BC.
∴四边形ABCD是平行四边形.
//
=
//
=
//
=
思考:四边形AEFD和EBCF都是平行四边形,求证四边形ABCD 是平行四边形.
提示:要由其中的一个或多个平行四边形,得出四边形中边角的条件,判定其他四边形也是平行四边形
平行四边形性质与判定的综合运用
A
B
C
D
E
F
例题讲解
已知,如图,在平行四边形ABCD中,BN=DM,BE=DF.求证:四边形MENF是平行四边形.
证明:在平行四边形ABCD中,AD∥BC,
∴∠MDF=∠NBE.
∵DM=BN,DF=BE,
∴△MDF≌△NBE(SAS).
∴MF=NE,∠MFD=∠NEB.
∴四边形MENF是平行四边形.
∴∠MFE=∠NEF ∴FM∥EN.
平行四边形性质与判定的综合运用
例
例题讲解
如图,已知四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F.
(1)求证:BE=DF;
(2)若M,N分别为边AD,BC上的点,且DM=BN,试判断四边形MENF的形状(不必说明理由)
证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD, ∴∠ABD=∠CDB,
∵AE⊥BD于E,CF⊥BD于F,
∴∠AEB=∠CFD=90°,
∴△ABE≌△CDF(AAS),
∴BE=DF;
变式训练
(2)四边形MENF是平行四边形.
由(1)可知:BE=DF,
∵四边形ABCD为平行四边行,∴AD∥BC,
∴∠MDB=MBD,
∵DM=BN,∴△DNF≌△BNE,
∴NE=MF,∠MFD=∠NEB,
∴∠MFE=∠NEF, ∴MF∥NE,
∴四边形MENF是平行四边形.
https://www.21cnjy.com/help/help_extract.php
6.2 平行四边形的判定
北师大版八年级下册数学
第六章平行四边形
学行四边形之后,小明回家用细木棒钉制了一个平行四边形.第二天,小明拿着自己动手做的平行四边形向同学们展示.
小辉却问:你凭什么确定这四边形就是平行四边形呢
大家都困惑了……
情景引入
活动1:用两根长30cm的木条和两根长20cm的木条作为四边形的四条边,能否拼成一个平行四边形?与同伴进行交流.
20cm
30cm
猜测:两组对边分别相等的四边形是平行四边形.
一、平行四边形的判定定理1
合作探究
已知: 四边形ABCD中,AB=CD,AD=CB.
求证: 四边形ABCD是平行四边形.
A
B
C
D
连接BD,
在△ABD和△CDB中,
AB=CD
BD=DB
AD=CB
∴△ABD≌△CDB(SSS).
∴ ∠1=∠2 , ∠ 3=∠4.
∴AB∥ CD , AD∥ CB
∴四边形ABCD是平行四边形.
证明:
1
4
2
3
合作探究
两组对边分别相等的四边形是平行四边形.
∵AB=CD,
AD=BC
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理1
B
D
C
A
总结归纳
例1 如图,在平行四边形ABCD中,E、F分别是边BC和AD上的两点,且AF=CE.
求证:四边形AECF为平行四边形
B
A
C
D
F
E
证明:可求得△ABE≌△CDF(SAS)
∴AE=CF
又∵AF=CE
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
典例精析
活动2:将两根同样长的木条AD,BC平行放置,再用木条AB,DC加固,得到的四边形ABCD是平行四边形.
A
B
C
D
猜想:一组对边平行且相等的四边形是平行四边形.
二、平行四边形的判定定理2
探究新知
连接AC.
∵AB//CD, ∴∠1=∠2.
又AB=CD,AC=CA,
∴△ABC≌△CDA(SAS).
∴BC=DA.
∴四边形ABCD的两组对边分别相等,它是平行四边形.
D
A
B
C
已知:如图,在四边形ABCD中,AB//CD.
求证:四边形ABCD是平行四边形.
证明:
1
2
探究新知
一组对边平行且相等的四边形是平行四边形.
∵AB=CD,
AB∥CD
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理2
B
D
C
A
总结归纳
例2 如图,在平行四边形ABCD中,已知AE、CF分别是∠DAB、∠BCD的角平分线,试证明四边形AFCE是平行四边形.
证明:∵在平行四边形ABCD中,
AE、CF分别是∠DAB、 ∠BCD的角平分线
∴∠B=∠D,AB=CD, AD∥BC
∠BAE=∠DCF= ∠DAB= ∠BCD
∴△ABE≌△CDF(ASA)
∴BE=DF∴AF=CE ∵AF∥CE
∴四边形AFCE是平行四边形(一组对边平行且相等的四边形是平行四边形)
例题讲解
卢师傅要做一个平行四边形木框.他要从图中几根木条中选出四根来制作,可是他不知道该怎样选,请同学们帮他选一选,哪四根木条可以制作成平行四边形木框,为什么?
7cm
4cm
3cm
3cm
5cm
4cm
阅读思考
4cm
4cm
4cm
4cm
3cm
3cm
3cm
3cm
发现:一组对边平行,另一组对边相等的四边形不一定是平行四边形.
活动:
有一名同学将两根木条的中点重叠,并用钉子固定,得到如图的四边形,你认为这个四边形是平行四边形吗?
活动探究:做一做 :小组活动,回答下列问题。(小组讨论,3min)
三、平行四边形的判定定理3
探究新知
现在将你手中两根长度不等的细木条摆放在一张纸上,能否使得这两根细木条的四个端点恰好是一个平行四边形的四个顶点呢 做一做,与同伴交流.
活动探究:做一做 :小组活动,回答下列问题。(小组讨论,3min)
探究新知
已知:如图6-12,四边形ABCD的对角线AC、BD相交于点O,并且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
探究新知
证明: ∵ OA=OC,OD=OB,
∠AOD=∠COB,
∴ △AOD≌△COB.
∴ AD=CB,∠ADO=∠CBO,
∵ ∠ADO=∠CBO
∴ AD∥CB
∵ AD=CB且AD∥CB
∴ 四边形ABCD是平行四边形.
(一组对边平行且相等的四边形是平行四边形)
探究新知
思考:以上活动事实,能用文字语言表达吗?
平行四边形判定定理3:
对角线互相平分的四边形是平行四边形。
以上定理转换成数学语言是
如图
∵ OA=OC,OB=OD
∴ 四边形ABCD是平行四边形.
探究新知
例2:已知,如图6-13(1),在平行四边形ABCD中,
点E、F在对角线AC上,并且AE=CF.
求证:四边形BFDE是平行四边形吗?
证明: 如图,连接BD,交AC于点O.
∵ 四边形ABCD是平行四边形
∴ OA=OC,OB=OD.
又∵AE=CF
∴OA-AE=OC-CF,即OE=OF.
∴四边形BFDE是平行四边形.
(对角线互相平分的四边形是平行四边形)
探究新知
如图,在平行四边形ABCD中,对角线AC与BD相交于点O,E、F分别是OA和OC的中点,四边形BFDE是平行四边形吗?请说明理由。
探究新知
证明:∵四边形ABCD是平行四边形
∴OD=OB,OA=OC
∵E、F分别是AO、CO的中点
∴OE= OA,OF= OC
∴OE=OF
∴四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形)
2
1
2
1
探究新知
变式2:若E、F移至OA、OC的延长线上,且AE=CF,结论有改变吗?为什么?
探究新知
证明:∵四边形ABCD是平行四边形
∴OD=OB,OA=OC
∵ AE=CF
∴OE=OA+AE,OF=OC+CF
∴OE=OF
∴四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形)
探究新知
思考:我们可以从角出发来判定一个四边形是否为平行四边形吗?
A
B
C
D
你能根据平行四边形的定义证明它们吗?
四、由定义判定平行四边形
探究新知
已知:四边形ABCD中,∠A=∠C,∠B=∠D,
求证:四边形ABCD是平行四边形.
A
B
C
D
又∵∠A=∠C,∠B=∠D
∵∠A+∠C+∠B+∠D=360°
∴2∠A+2∠B=360°
即∠A+∠B=180°
∴ AD∥BC
∴四边形ABCD是平行四边形.
同理得 AB∥ CD
证明:
定义判定:
两组对角分别相等的四边形是平行四边形
探究新知
归纳小结
判定
定理1
定理2
定义判定
文字语言
图形语言
符号语言
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
平行四边形判定定理
A
B
C
D
∵AB=CD,AD=BC,
∴四边形ABCD是
ABCD
A
B
C
D
∵ AB= CD,
AB∥CD,
∴四边形ABCD是
ABCD
A
B
C
D
O
∵ ∠ A= ∠ C,
∠ B= ∠ D,
∴四边形ABCD是
ABCD
如图,在方格纸上画两条互相平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线,用刻度尺度量出平行线之间的垂线段的长度.
经过度量,我们发现这些垂线段的长度都相等(从图中也可以看到这一点).
猜想:平行线间距离处处相等.
活动:
平行线之间的距离
五、平行线之间的距离
探究新知
如图,直线a//b,A,B是直线a上任意两点,AC⊥b,BD⊥b,垂足分别为C,D.求证:AC=BD.
证明:∵AC⊥CD,BD⊥CD,
∴∠1=∠2=90°.
∴AC∥BD.
∵ AB∥CD,
∴四边形ACDB是平行四边形.
∴AC=BD.
a
b
A
B
C
D
1
2
猜想证明:
探究新知
如果两条直线互相平行,则其中一条直线上任意一点到另一条直线的距离都相等(如图:AC=BD),这个距离称为平行线之间的距离.
(简记为:两条平行线间的距离处处相等).
结论
探究新知
A
B
思考:两条平行线之间的距离与点和点之间的距离、点到线之间的距离有何区别与联系?
a
b
A
B
点到直线的距离只有一条,即过直线外一点作直线的垂线段的长度;而平行线的距离有无数条即一直线上任一点都可以得到一条两平行直线的距离.
结论
A
B
探究新知
思考:若垂线段改为夹在两条平行线间的平行线段呢?它们是否相等呢?
由“两组对边分别平行的四边形是平行四边形”易知其围成的封闭图形为平行四边形,再由平行四边形性质易知夹在两条平行线间的平行线段相等.
结论
探究新知
例 如图,甲船从北岸码头A向南行驶,航速为36千米/时;乙船从南岸码头B向北行驶,航速为27千米/时.两船均于7:15出发,两岸平行,水面宽为18.9千米,求两船距离最近时的时刻.
平行线之间的距离
例题讲解
解:设x分钟后两船距离最近,
当如图EF⊥BD,AE = DF时,两船距离最近,
根据题意得出:36x=18.9-27x, 解得x=0.3,
0.3小时=0.3×60分钟=18(分钟),
则两船距离最近时的时刻为7:33.
例题讲解
方法总结
平行线之间的距离概念辨析
注意:平行线之间的距离是指其中一条直线上的点到另一条直线的距离,是垂线段的长度,而不是垂线段.
作法:从其中一条直线上任意找一点,向另一条直线作垂线,垂线段的长度即平行线之间的距离.
如图,直线AE//BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为 .
A
B
C
D
E
分析:根据平行线之间的距离处处相等.
解析:设高为h,则S△ABD= ·BD·h=16,所以h=4,
所以S △ACE= ·AE·h= ×5 ×4=10.
10
变式训练
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD EF,EF BC.
∴AD BC.
∴四边形ABCD是平行四边形.
//
=
//
=
//
=
思考:四边形AEFD和EBCF都是平行四边形,求证四边形ABCD 是平行四边形.
提示:要由其中的一个或多个平行四边形,得出四边形中边角的条件,判定其他四边形也是平行四边形
平行四边形性质与判定的综合运用
A
B
C
D
E
F
例题讲解
已知,如图,在平行四边形ABCD中,BN=DM,BE=DF.求证:四边形MENF是平行四边形.
证明:在平行四边形ABCD中,AD∥BC,
∴∠MDF=∠NBE.
∵DM=BN,DF=BE,
∴△MDF≌△NBE(SAS).
∴MF=NE,∠MFD=∠NEB.
∴四边形MENF是平行四边形.
∴∠MFE=∠NEF ∴FM∥EN.
平行四边形性质与判定的综合运用
例
例题讲解
如图,已知四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F.
(1)求证:BE=DF;
(2)若M,N分别为边AD,BC上的点,且DM=BN,试判断四边形MENF的形状(不必说明理由)
证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD, ∴∠ABD=∠CDB,
∵AE⊥BD于E,CF⊥BD于F,
∴∠AEB=∠CFD=90°,
∴△ABE≌△CDF(AAS),
∴BE=DF;
变式训练
(2)四边形MENF是平行四边形.
由(1)可知:BE=DF,
∵四边形ABCD为平行四边行,∴AD∥BC,
∴∠MDB=MBD,
∵DM=BN,∴△DNF≌△BNE,
∴NE=MF,∠MFD=∠NEB,
∴∠MFE=∠NEF, ∴MF∥NE,
∴四边形MENF是平行四边形.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
