沪科版数学八年级下册 18.1 勾股定理-教案
文档属性
| 名称 | 沪科版数学八年级下册 18.1 勾股定理-教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 110.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 10:06:33 | ||
图片预览

文档简介
勾股定理
一、教学目标:
(1)知识与技能:了解勾股定理的产生背景,体验勾股定理的探索过程,掌握验证勾股定理的方法;了解勾股定理的内容;能利用已知两边求直角三角形另一边的长;
(2)过程与方法:在勾股定理的探索过程中,培养合情推理能力,体会数形结合和从特殊到一般的思想;
(3)情感与态度:在探索勾股定理的过程中,体验获得结论的快乐,培养合作意识和探索精神。
二、教学重、难点:
重点:探索和证明勾股定理
难点:用拼图方法证明勾股定理
三、教学过程:
一、创设情境,导入新课
相传2500年前,毕达哥拉斯有一次在朋友家作客时,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.相传2500年前,毕达哥拉斯有一次在朋友家作客时,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.
二、探究勾股定理
1、探究等腰直角三角形的三边之间的特殊关系
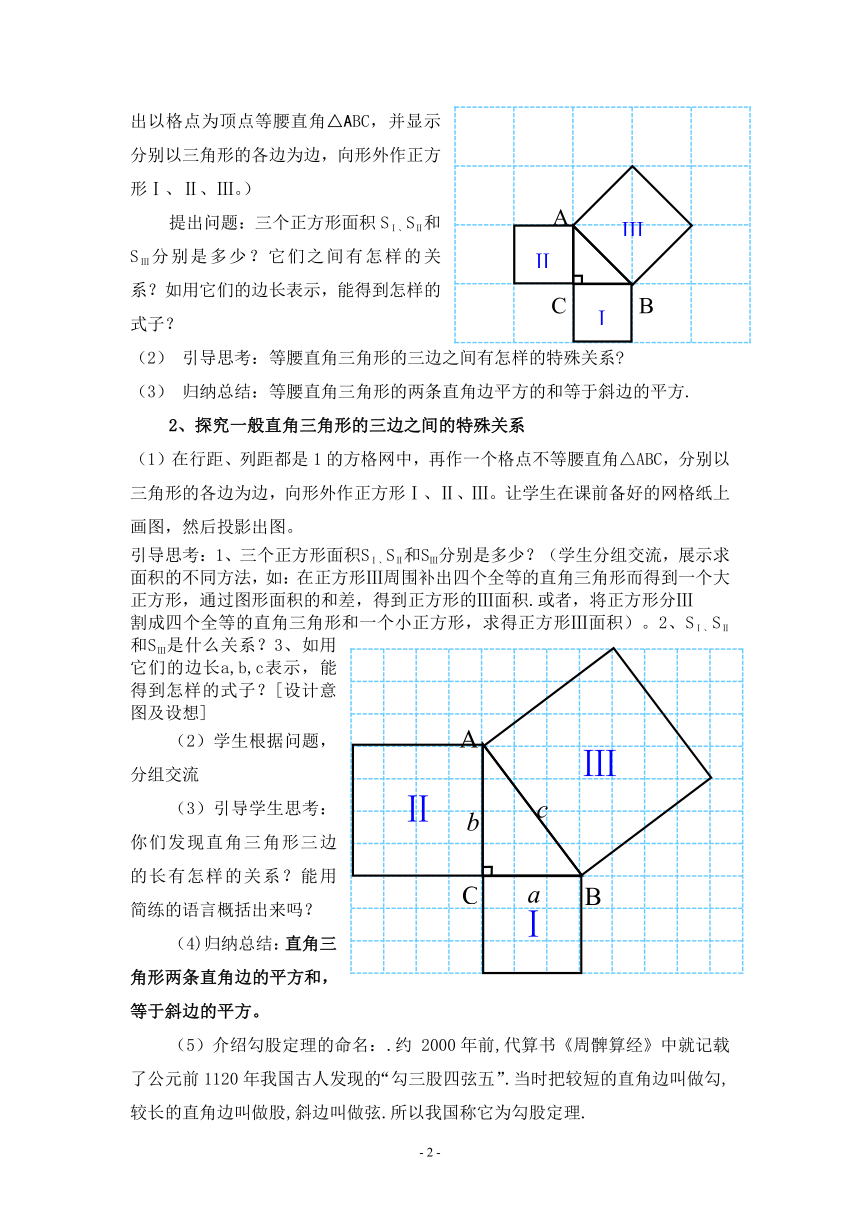
(1)展示图片:(如图是一个行距、列距都是1的方格网。在方格网中投影显示出以格点为顶点等腰直角△ABC,并显示分别以三角形的各 (
Ⅰ
Ⅱ
Ⅲ
A
C
B
)边为边,向形外作正方形Ⅰ、Ⅱ、Ⅲ。)
提出问题:三个正方形面积SⅠ、SⅡ和SⅢ分别是多少?它们之间有怎样的关系?如用它们的边长表示,能得到怎样的式子?
引导思考:等腰直角三角形的三边之间有怎样的特殊关系
归纳总结:等腰直角三角形的两条直角边平方的和等于斜边的平方.
2、探究一般直角三角形的三边之间的特殊关系
(1)在行距、列距都是1的方格网中,再作一个格点不等腰直角△ABC,分别以三角形的各边为边,向形外作正方形Ⅰ、Ⅱ、Ⅲ。让学生在课前备好的网格纸上画图,然后投影出图。
引导思考:1、三个正方形面积SⅠ、SⅡ和SⅢ分别是多少?(学生分组交流,展示求面积的不同方法,如:在正方形Ⅲ周围补出四个全等的直角三角形而得到一个大正方形,通过图形面积的和差,得到正方形的Ⅲ面积.或者,将正方形分Ⅲ
割成四个全等的直角三角形和一个小正方形,求得正方形Ⅲ面积)。2、SⅠ、SⅡ和SⅢ是什么关系? (
A
C
B
c
b
a
Ⅰ
Ⅱ
Ⅲ
)3、如用它们的边长a,b,c表示,能得到怎样的式子?[设计意图及设想]
(2)学生根据问题,分组交流
(3)引导学生思考:你们发现直角三角形三边的长有怎样的关系?能用简练的语言概括出来吗?
(4)归纳总结:直角三角形两条直角边的平方和,等于斜边的平方。
(5)介绍勾股定理的命名:.约 2000年前,代算书《周髀算经》中就记载了公元前1120年我国古人发现的“勾三股四弦五”.当时把较短的直角边叫做勾, 较长的直角边叫做股,斜边叫做弦.所以我国称它为勾股定理.
西方国家称勾股定理为毕达哥拉斯定理。
三、证明勾股定理
1、介绍古今中外数学家和数学爱好者对勾股定理研究和证明的历史.
2、引导学生证明勾股定理:如图在直角△ABC中,∠C=90°AB=C,BC=a, AC=b,
求证:a2+b2=c2
3、向学生介绍下列两种证明勾股定理的方法,激发学生的兴趣
(方法一)以a、b 为直角边,以c为斜边做四个全等的直角三角形,则每个直角三角形的面积等于. 把这四个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上,B、F、C三点在一条直线上,C、G、D三点在一条直线上.
∵ RtΔHAE ≌ RtΔEBF,
∴ ∠AHE = ∠BEF.
∵ ∠AEH + ∠AHE = 90 ,
∴ ∠AEH + ∠BEF = 90 .
∴ ∠HEF = 180 ―90 = 90 .
∴ 四边形EFGH是一个边长为c的
正方形. 它的面积等于c2.
∵ RtΔGDH ≌ RtΔHAE,
∴ ∠HGD = ∠EHA.
∵ ∠HGD + ∠GHD = 90 ,
∴ ∠EHA + ∠GHD = 90 .
又∵ ∠GHE = 90 ,
∴ ∠DHA = 90 + 90 = 180 .
∴ ABCD是一个边长为a + b的正方形,它的面积等于.
∴ . ∴ .
(方法二):将四个全等的直角三角形拼成如图所示的正方形,
(方法三):如图所示将两个直角三角形拼成直角梯形(美国总统的证明方法)
由
.得
四、巩固练习
如图,在Rt△ABC中,∠ACB = ,BC=12, AC=5,
(1)求AB的长. (2)求AB边上的高的长。
(
A
C
B
)
五、课堂小结:
1、通过这节课的学习,你有哪些收获?
2、你会用学过的内容解决课前的问题吗?
六、布置作业:
课后作业1、2
- 4 -
一、教学目标:
(1)知识与技能:了解勾股定理的产生背景,体验勾股定理的探索过程,掌握验证勾股定理的方法;了解勾股定理的内容;能利用已知两边求直角三角形另一边的长;
(2)过程与方法:在勾股定理的探索过程中,培养合情推理能力,体会数形结合和从特殊到一般的思想;
(3)情感与态度:在探索勾股定理的过程中,体验获得结论的快乐,培养合作意识和探索精神。
二、教学重、难点:
重点:探索和证明勾股定理
难点:用拼图方法证明勾股定理
三、教学过程:
一、创设情境,导入新课
相传2500年前,毕达哥拉斯有一次在朋友家作客时,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.相传2500年前,毕达哥拉斯有一次在朋友家作客时,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.
二、探究勾股定理
1、探究等腰直角三角形的三边之间的特殊关系
(1)展示图片:(如图是一个行距、列距都是1的方格网。在方格网中投影显示出以格点为顶点等腰直角△ABC,并显示分别以三角形的各 (
Ⅰ
Ⅱ
Ⅲ
A
C
B
)边为边,向形外作正方形Ⅰ、Ⅱ、Ⅲ。)
提出问题:三个正方形面积SⅠ、SⅡ和SⅢ分别是多少?它们之间有怎样的关系?如用它们的边长表示,能得到怎样的式子?
引导思考:等腰直角三角形的三边之间有怎样的特殊关系
归纳总结:等腰直角三角形的两条直角边平方的和等于斜边的平方.
2、探究一般直角三角形的三边之间的特殊关系
(1)在行距、列距都是1的方格网中,再作一个格点不等腰直角△ABC,分别以三角形的各边为边,向形外作正方形Ⅰ、Ⅱ、Ⅲ。让学生在课前备好的网格纸上画图,然后投影出图。
引导思考:1、三个正方形面积SⅠ、SⅡ和SⅢ分别是多少?(学生分组交流,展示求面积的不同方法,如:在正方形Ⅲ周围补出四个全等的直角三角形而得到一个大正方形,通过图形面积的和差,得到正方形的Ⅲ面积.或者,将正方形分Ⅲ
割成四个全等的直角三角形和一个小正方形,求得正方形Ⅲ面积)。2、SⅠ、SⅡ和SⅢ是什么关系? (
A
C
B
c
b
a
Ⅰ
Ⅱ
Ⅲ
)3、如用它们的边长a,b,c表示,能得到怎样的式子?[设计意图及设想]
(2)学生根据问题,分组交流
(3)引导学生思考:你们发现直角三角形三边的长有怎样的关系?能用简练的语言概括出来吗?
(4)归纳总结:直角三角形两条直角边的平方和,等于斜边的平方。
(5)介绍勾股定理的命名:.约 2000年前,代算书《周髀算经》中就记载了公元前1120年我国古人发现的“勾三股四弦五”.当时把较短的直角边叫做勾, 较长的直角边叫做股,斜边叫做弦.所以我国称它为勾股定理.
西方国家称勾股定理为毕达哥拉斯定理。
三、证明勾股定理
1、介绍古今中外数学家和数学爱好者对勾股定理研究和证明的历史.
2、引导学生证明勾股定理:如图在直角△ABC中,∠C=90°AB=C,BC=a, AC=b,
求证:a2+b2=c2
3、向学生介绍下列两种证明勾股定理的方法,激发学生的兴趣
(方法一)以a、b 为直角边,以c为斜边做四个全等的直角三角形,则每个直角三角形的面积等于. 把这四个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上,B、F、C三点在一条直线上,C、G、D三点在一条直线上.
∵ RtΔHAE ≌ RtΔEBF,
∴ ∠AHE = ∠BEF.
∵ ∠AEH + ∠AHE = 90 ,
∴ ∠AEH + ∠BEF = 90 .
∴ ∠HEF = 180 ―90 = 90 .
∴ 四边形EFGH是一个边长为c的
正方形. 它的面积等于c2.
∵ RtΔGDH ≌ RtΔHAE,
∴ ∠HGD = ∠EHA.
∵ ∠HGD + ∠GHD = 90 ,
∴ ∠EHA + ∠GHD = 90 .
又∵ ∠GHE = 90 ,
∴ ∠DHA = 90 + 90 = 180 .
∴ ABCD是一个边长为a + b的正方形,它的面积等于.
∴ . ∴ .
(方法二):将四个全等的直角三角形拼成如图所示的正方形,
(方法三):如图所示将两个直角三角形拼成直角梯形(美国总统的证明方法)
由
.得
四、巩固练习
如图,在Rt△ABC中,∠ACB = ,BC=12, AC=5,
(1)求AB的长. (2)求AB边上的高的长。
(
A
C
B
)
五、课堂小结:
1、通过这节课的学习,你有哪些收获?
2、你会用学过的内容解决课前的问题吗?
六、布置作业:
课后作业1、2
- 4 -
