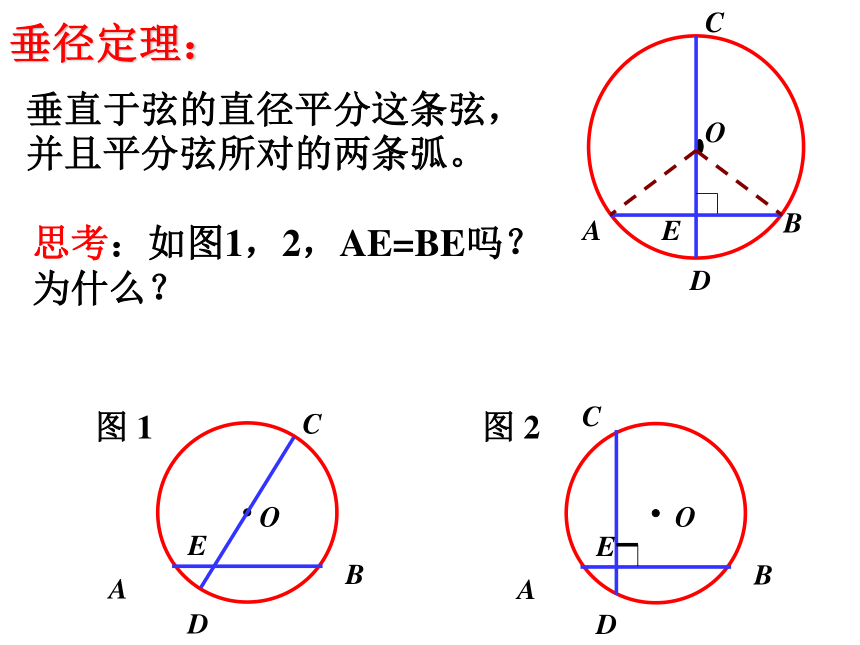
垂径定理
图片预览


文档简介
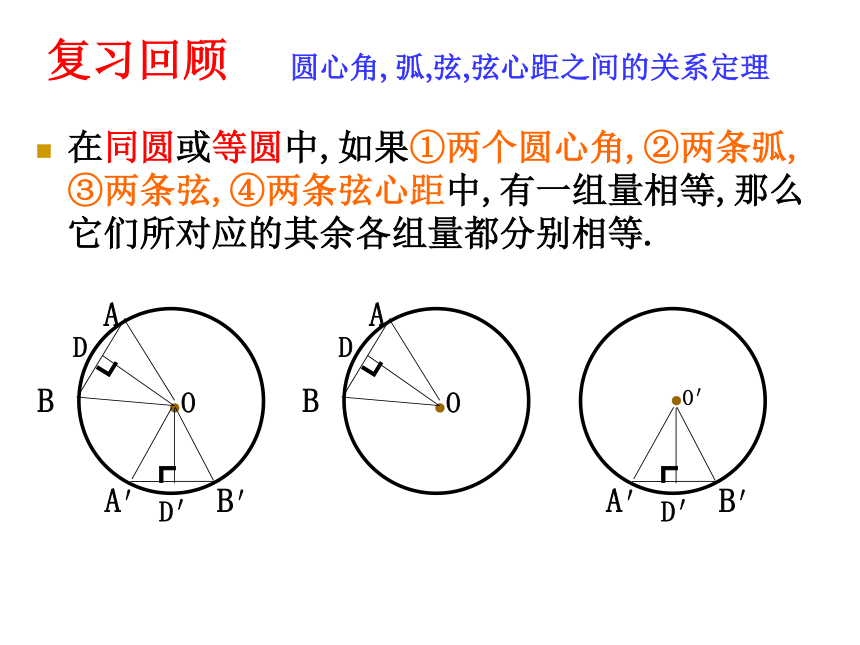
课件19张PPT。复习回顾在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.圆心角, 弧,弦,弦心距之间的关系定理 第28章 圆28.1.2 圆的对称性 (2)
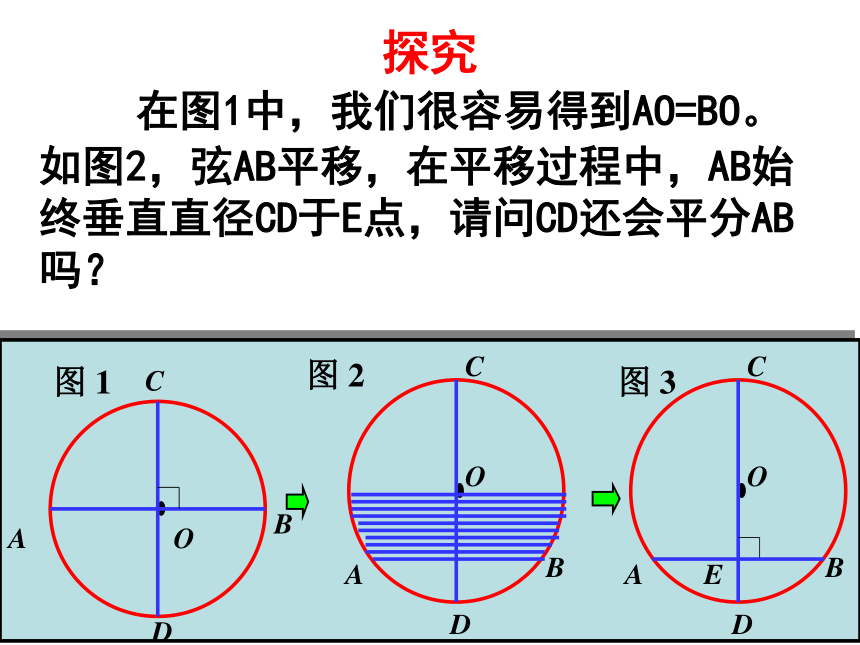
垂径定理图 1图 2图 3探究
在图1中,我们很容易得到AO=BO。
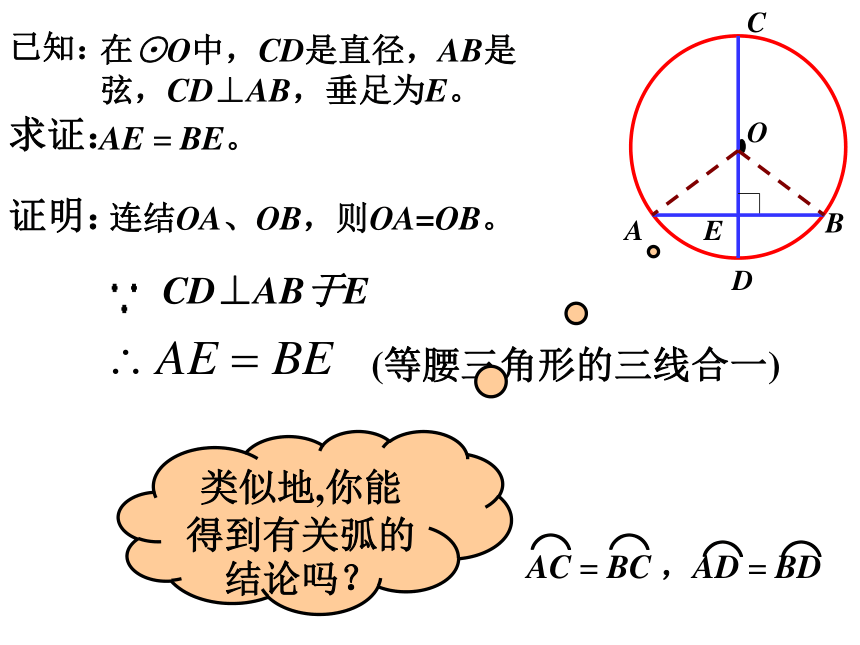
如图2,弦AB平移,在平移过程中,AB始终垂直直径CD于E点,请问CD还会平分AB吗?AE = BE。求证:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。已知:证明:连结OA、OB,则OA=OB。 CD⊥AB于E(等腰三角形的三线合一)类似地,你能得到有关弧的结论吗?AE = BE,求证:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。已知:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。垂径定理:垂径定理条件:1、CD为直径
2、CD⊥AB3、AE = BE
4、
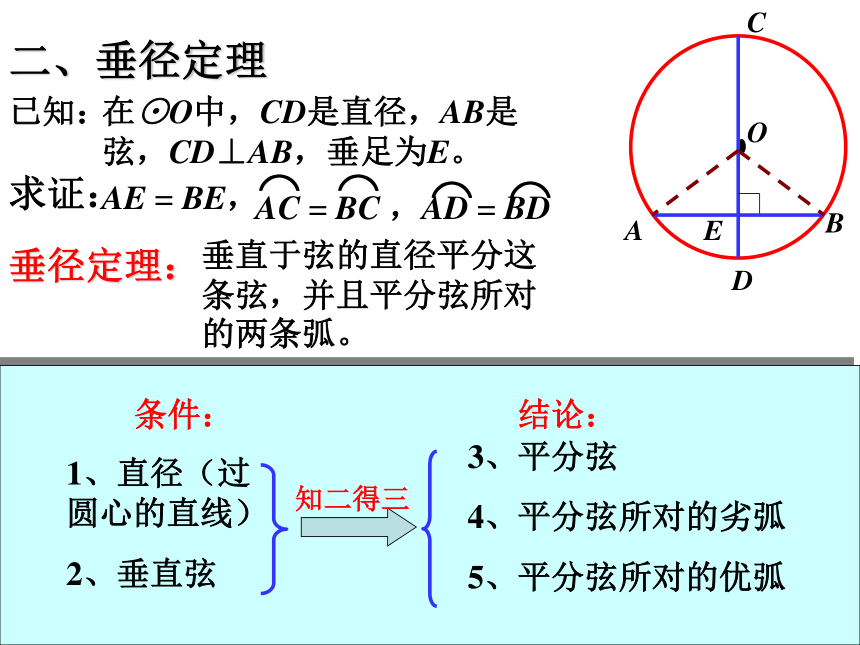
5、 结论:(CD平分弦AB)(CD平分弧ACB)(CD平分弧AB)知二得三AE = BE,求证:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。已知:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。垂径定理:二、垂径定理条件: 结论:1、直径(过圆心的直线)
2、垂直弦3、平分弦
4、平分弦所对的劣弧
5、平分弦所对的优弧知二得三 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。垂径定理:思考:如图1,2,AE=BE吗?为什么?②CD⊥AB,垂径定理的推论AB是⊙O的一条弦,且AM=BM.你能发现图中有哪些结论?与同伴说说你的想法和理由.过点M作直径CD.由 ① CD是直径③ AM=BM┗平分弦 的直径垂直于弦,并且平分弦所对的两条弧.(不是直径)垂径定理的结论如图,在下列五个条件中:① CD是直径,③ AM=BM,② CD⊥AB,垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。平分弦 的直径垂直于弦,并且平 分弦所对的两条弧.(不是直径)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.垂径定理的推论:你可以写出相应的命题吗?
相信自己是最棒的!垂径定理的其余结论如图,在下列五个条件中:只要具备其中两个条件,就可推出其余三个结论.① CD是直径,③ AM=BM,② CD⊥AB,垂直于弦的直径平分弦,并且平分弦所对的两条弧.平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧. 垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.① CD是直径,② CD⊥AB,③ AM=BM,(1)垂直于弦的直线平分弦,并且平分弦所对的两条弧( )(2)弦所对的两弧中点的连线,垂直于弦,并且经过圆心。 ( )(3)圆的不与直径垂直的弦必不被这条直径平分.( )(4)平分弦的直径垂直于弦,并且平分弦所对的两条弧。( )×××√判断:(5)平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( )√(7)平分弦的直径,平分这条弦所对的弧( )(8)平分弦的直线,必定过圆心。( )(9)一条直线平分弦(这条弦不是直径),那么这
条直线垂直这条弦。 ( )×××例 1、如图,已知在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径。解:连结OA。过O作OE⊥AB,垂足为E,则OE=3cm, AE=BE.∵AB=8cm∴AE=4cm∴⊙O的半径为5cm辅助线:半径,弦心距,弦三者构造直角三角形 例2、如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点。
求证:AC = BDE证明:过O作OE⊥AB,垂足为E, 则AE = BE, CE = DE∴AE - CE = BE - DE
即 AC = BD注意:解决有关弦的问题,过圆心作弦的垂线,是一种常用的辅助线添法。 ABCDO1、如图1,在⊙O中, AB是 弦, OC = OD。
求证:AC = BD (1)ABCDO2、如图2,在⊙O中, CD是
弦, OA = OB。
求证:AC = BD (2)练习4.已知:如图,在⊙O中,AB、AC为互相垂直的两条相等的弦,OD⊥AB,OE⊥AC,D、E为垂足。求证:ADOE为正方形。3. 在半径为50mm的⊙O中,有长50mm的弦AB。计算:(1) 点O与AB的距离;(2)∠AOB的度数。练习 小 结谢谢
垂径定理图 1图 2图 3探究
在图1中,我们很容易得到AO=BO。
如图2,弦AB平移,在平移过程中,AB始终垂直直径CD于E点,请问CD还会平分AB吗?AE = BE。求证:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。已知:证明:连结OA、OB,则OA=OB。 CD⊥AB于E(等腰三角形的三线合一)类似地,你能得到有关弧的结论吗?AE = BE,求证:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。已知:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。垂径定理:垂径定理条件:1、CD为直径
2、CD⊥AB3、AE = BE
4、
5、 结论:(CD平分弦AB)(CD平分弧ACB)(CD平分弧AB)知二得三AE = BE,求证:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。已知:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。垂径定理:二、垂径定理条件: 结论:1、直径(过圆心的直线)
2、垂直弦3、平分弦
4、平分弦所对的劣弧
5、平分弦所对的优弧知二得三 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。垂径定理:思考:如图1,2,AE=BE吗?为什么?②CD⊥AB,垂径定理的推论AB是⊙O的一条弦,且AM=BM.你能发现图中有哪些结论?与同伴说说你的想法和理由.过点M作直径CD.由 ① CD是直径③ AM=BM┗平分弦 的直径垂直于弦,并且平分弦所对的两条弧.(不是直径)垂径定理的结论如图,在下列五个条件中:① CD是直径,③ AM=BM,② CD⊥AB,垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。平分弦 的直径垂直于弦,并且平 分弦所对的两条弧.(不是直径)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.垂径定理的推论:你可以写出相应的命题吗?
相信自己是最棒的!垂径定理的其余结论如图,在下列五个条件中:只要具备其中两个条件,就可推出其余三个结论.① CD是直径,③ AM=BM,② CD⊥AB,垂直于弦的直径平分弦,并且平分弦所对的两条弧.平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧. 垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.① CD是直径,② CD⊥AB,③ AM=BM,(1)垂直于弦的直线平分弦,并且平分弦所对的两条弧( )(2)弦所对的两弧中点的连线,垂直于弦,并且经过圆心。 ( )(3)圆的不与直径垂直的弦必不被这条直径平分.( )(4)平分弦的直径垂直于弦,并且平分弦所对的两条弧。( )×××√判断:(5)平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( )√(7)平分弦的直径,平分这条弦所对的弧( )(8)平分弦的直线,必定过圆心。( )(9)一条直线平分弦(这条弦不是直径),那么这
条直线垂直这条弦。 ( )×××例 1、如图,已知在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径。解:连结OA。过O作OE⊥AB,垂足为E,则OE=3cm, AE=BE.∵AB=8cm∴AE=4cm∴⊙O的半径为5cm辅助线:半径,弦心距,弦三者构造直角三角形 例2、如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点。
求证:AC = BDE证明:过O作OE⊥AB,垂足为E, 则AE = BE, CE = DE∴AE - CE = BE - DE
即 AC = BD注意:解决有关弦的问题,过圆心作弦的垂线,是一种常用的辅助线添法。 ABCDO1、如图1,在⊙O中, AB是 弦, OC = OD。
求证:AC = BD (1)ABCDO2、如图2,在⊙O中, CD是
弦, OA = OB。
求证:AC = BD (2)练习4.已知:如图,在⊙O中,AB、AC为互相垂直的两条相等的弦,OD⊥AB,OE⊥AC,D、E为垂足。求证:ADOE为正方形。3. 在半径为50mm的⊙O中,有长50mm的弦AB。计算:(1) 点O与AB的距离;(2)∠AOB的度数。练习 小 结谢谢
