直线与圆的位置关系
图片预览





文档简介
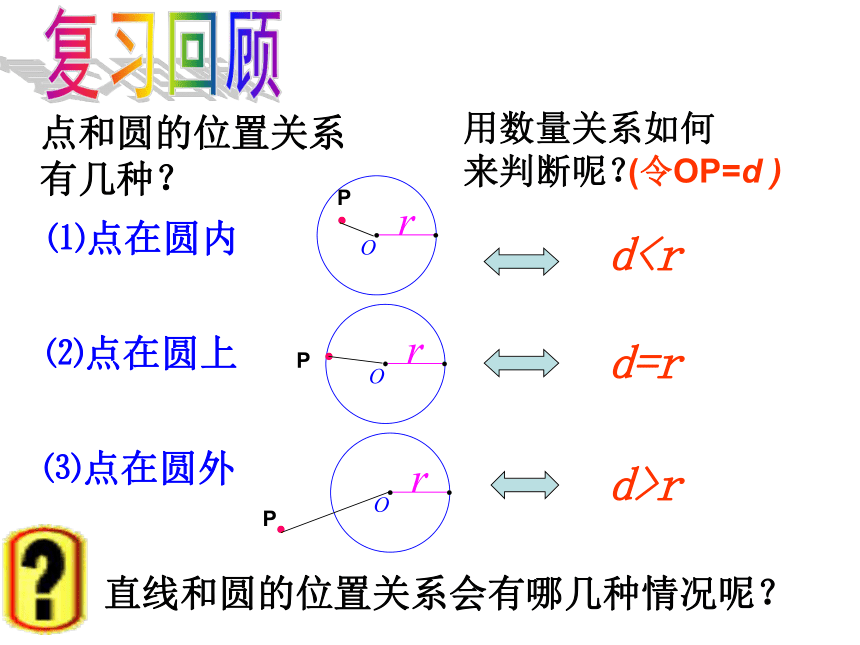
课件23张PPT。点和圆的位置关系有几种?dr用数量关系如何来判断呢?复习回顾⑴点在圆内⑵点在圆上⑶点在圆外(令OP=d )直线和圆的位置关系会有哪几种情况呢?直线与圆的位置关系试一试
1.在纸上画一条直线,把硬币的边缘看
作圆,在纸上移动硬币.
2.在纸上画一个圆,把直尺看作直线,
移动直尺。
你能发现直线与圆的公共点个数的变化情况吗?公共点最少时有几个?最多时有几个? 通过实验,你认为直线和圆的位置关系会有哪几种情况?.Ol特点:.O叫做直线和圆相离。直线和圆没有公共点,l特点:直线和圆有唯一的公共点,叫做直线和圆相切。这时的直线叫切线,
唯一的公共点叫切点。.Ol特点:直线和圆有两个公共点,叫直线和圆相交,这时的直线叫做圆的割线。一、直线与圆的位置关系
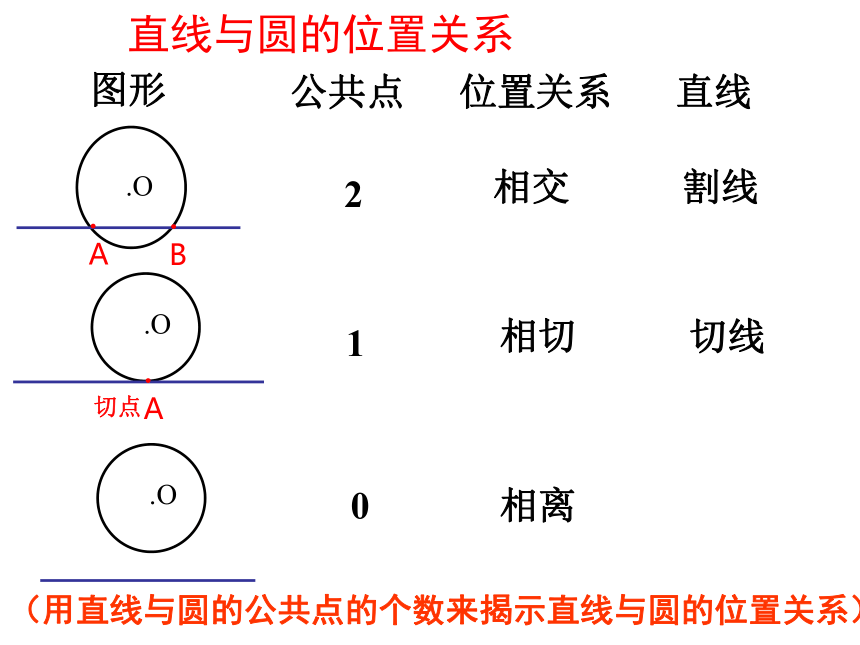
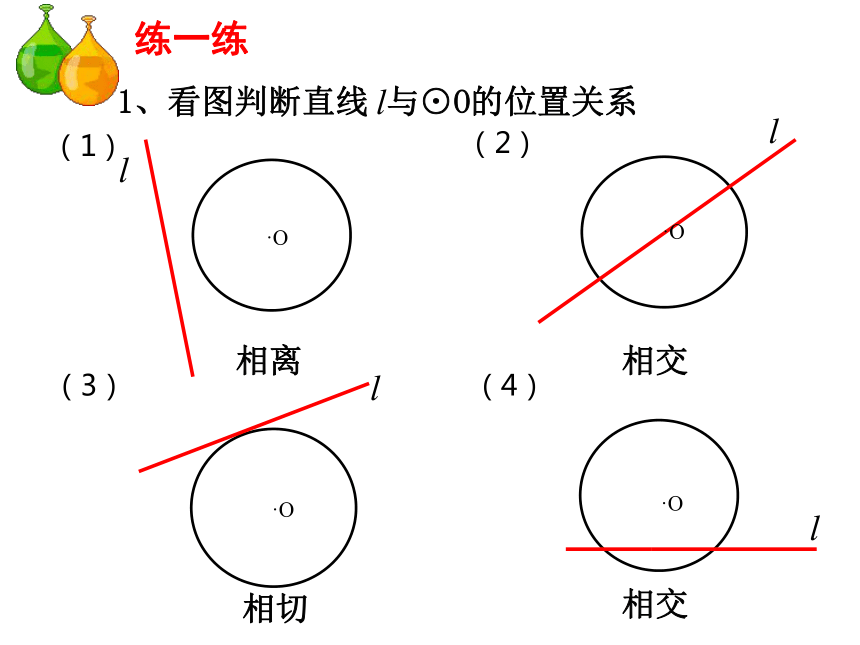
(用公共点的个数来区分).A.A.B切点.O.O直线与圆的位置关系.A切点图形切线12割线直线公共点0相交相切相离位置关系(用直线与圆的公共点的个数来揭示直线与圆的位置关系)练一练1、看图判断直线 与⊙O的位置关系(1)(2)(3)(4)相离相切相交相交·O·O·O·O是是非非1、直线与圆最多有两个公共点 。( ) √×2、若C为⊙O上的一点,则过点C的直线与⊙O
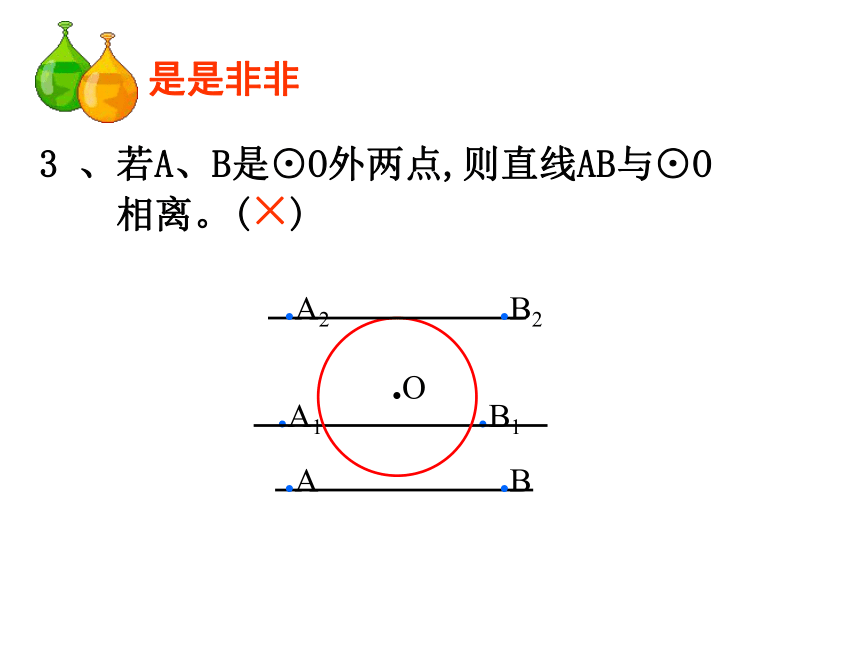
相切.( )是是非非3 、若A、B是⊙O外两点,则直线AB与⊙O
相离。( )
×4、若C为⊙O内一点,则过点C的直线与⊙O
相交( )
是是非非√1、如果公共点的个数不好判断,该怎么办? ·O·
A·
B2、“直线和圆的位置关系”能否像
“点和圆的位置关系”一样进行数量分析?想一想图中直线与圆有怎样的位置关系?2、直线和圆相切d = r3、直线和圆相交d < rdr直线和圆的位置关系1、直线和圆相离d > r(用圆心到直线的距离d和圆半径r的数量关系,
来揭示圆和直线的位置关系) 2)若d=6.5cm ,则直线与圆______,
直线与圆有____个公共点. 1、已知圆的直径为13cm,设直线和圆心的距离为d :3)若d= 8 cm ,则直线与圆______,
直线与圆有____个公共点. 1)若d=4.5cm ,则直线与圆 ,
直线与圆有____个公共点. 相交相切相离210填一填2、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d,根据条件填写d的范围:
1)若AB和⊙O相离,则 ;
2)若AB和⊙O相切, 则 ;
3)若AB和⊙O相交, 则 ; d > 5cmd = 5cm0cm≤d < 5cm3、直线l与半径为r的⊙O相交,且点O到直线l的距离为8,则r的取值范围是 .填一填r>8 在Rt△ABC中,∠C = 90°,AC = 3 cm ,
BC = 4 cm , 以C为圆心,r为半径的圆与AB有
怎样的关系?为什么?
(1)r = 2 cm ;
(2)r = 2.4 cm ;
(3)r = 3 cm .例解:过C作CD⊥AB于D,在Rt△ABC中,根据三角形面积公式有CD · AB = AC · BC即圆心C到AB的距离 d = 2.4 cm.(1)当r = 2cm 时,有d>r ,因此⊙C和AB相离. (2)当r = 2.4 cm时,有d=r ,因此⊙C和AB相切. (3)当r = 3 cm时,有d (2)r=2.4cm
(3)r=3cm在Rt△ABC中,∠C=90°,
AC=3cm,BC=4cm,
以C为圆心,r为半径作圆。想一想?当r满足 ____
____________ 时,⊙C与线段AB只有一个公共点. r=2.4cmBCAD453d=2.4cm 或3cm且OM=5cm,以M为圆心,以r为半径的圆与直线
OA有怎样的位置关系?为什么?
(1)r=2.5cm. (2)r=2cm; (2)r=4cm; 大家动手,做一做解: 过点M作MN⊥OA于点N ∵ 在Rt△OMN中,
∠AOB=30°,OM=5cm.
∴ MN=2.5CM即圆心M到直线OA的距离d=2.5cm(2)当r=2cm时,
∵d> r,
∴⊙M与直线OA相离。 (3)当r=4cm时,
∵d< r,
∴⊙M与直线OA相交。(1)当r=2.5cm时,
∵d = r,
∴⊙M与直线OA相切。 判定直线 与圆的位置关系的方法有____种:(1)根据定义,由__________________
的个数来判断;(2)根据性质,由____________________
的关系来判断。在实际应用中,常采用第二种方法判定。两直线 与圆的公共点圆心到直线的距离d与半径r小结:0d>r1d=r切点切线2d 随堂检测
1.⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l
与⊙O没有公共点,则d为( ):
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线
和⊙O的位置关系是( ):
A.相离 B.相交 C.相切 D.相切或相交
3.判断:若直线和圆相切,则该直线和圆一定有一个公共点.( )
4.等边三角形ABC的边长为2,则以A为圆心,半径为1.73的圆
与直线BC的位置关系是 ,以A为圆心,
为半径的圆与直线BC相切.AC√相离
1.在纸上画一条直线,把硬币的边缘看
作圆,在纸上移动硬币.
2.在纸上画一个圆,把直尺看作直线,
移动直尺。
你能发现直线与圆的公共点个数的变化情况吗?公共点最少时有几个?最多时有几个? 通过实验,你认为直线和圆的位置关系会有哪几种情况?.Ol特点:.O叫做直线和圆相离。直线和圆没有公共点,l特点:直线和圆有唯一的公共点,叫做直线和圆相切。这时的直线叫切线,
唯一的公共点叫切点。.Ol特点:直线和圆有两个公共点,叫直线和圆相交,这时的直线叫做圆的割线。一、直线与圆的位置关系
(用公共点的个数来区分).A.A.B切点.O.O直线与圆的位置关系.A切点图形切线12割线直线公共点0相交相切相离位置关系(用直线与圆的公共点的个数来揭示直线与圆的位置关系)练一练1、看图判断直线 与⊙O的位置关系(1)(2)(3)(4)相离相切相交相交·O·O·O·O是是非非1、直线与圆最多有两个公共点 。( ) √×2、若C为⊙O上的一点,则过点C的直线与⊙O
相切.( )是是非非3 、若A、B是⊙O外两点,则直线AB与⊙O
相离。( )
×4、若C为⊙O内一点,则过点C的直线与⊙O
相交( )
是是非非√1、如果公共点的个数不好判断,该怎么办? ·O·
A·
B2、“直线和圆的位置关系”能否像
“点和圆的位置关系”一样进行数量分析?想一想图中直线与圆有怎样的位置关系?2、直线和圆相切d = r3、直线和圆相交d < rdr直线和圆的位置关系1、直线和圆相离d > r(用圆心到直线的距离d和圆半径r的数量关系,
来揭示圆和直线的位置关系) 2)若d=6.5cm ,则直线与圆______,
直线与圆有____个公共点. 1、已知圆的直径为13cm,设直线和圆心的距离为d :3)若d= 8 cm ,则直线与圆______,
直线与圆有____个公共点. 1)若d=4.5cm ,则直线与圆 ,
直线与圆有____个公共点. 相交相切相离210填一填2、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d,根据条件填写d的范围:
1)若AB和⊙O相离,则 ;
2)若AB和⊙O相切, 则 ;
3)若AB和⊙O相交, 则 ; d > 5cmd = 5cm0cm≤d < 5cm3、直线l与半径为r的⊙O相交,且点O到直线l的距离为8,则r的取值范围是 .填一填r>8 在Rt△ABC中,∠C = 90°,AC = 3 cm ,
BC = 4 cm , 以C为圆心,r为半径的圆与AB有
怎样的关系?为什么?
(1)r = 2 cm ;
(2)r = 2.4 cm ;
(3)r = 3 cm .例解:过C作CD⊥AB于D,在Rt△ABC中,根据三角形面积公式有CD · AB = AC · BC即圆心C到AB的距离 d = 2.4 cm.(1)当r = 2cm 时,有d>r ,因此⊙C和AB相离. (2)当r = 2.4 cm时,有d=r ,因此⊙C和AB相切. (3)当r = 3 cm时,有d
(3)r=3cm在Rt△ABC中,∠C=90°,
AC=3cm,BC=4cm,
以C为圆心,r为半径作圆。想一想?当r满足 ____
____________ 时,⊙C与线段AB只有一个公共点. r=2.4cmBCAD453d=2.4cm 或3cm
OA有怎样的位置关系?为什么?
(1)r=2.5cm. (2)r=2cm; (2)r=4cm; 大家动手,做一做解: 过点M作MN⊥OA于点N ∵ 在Rt△OMN中,
∠AOB=30°,OM=5cm.
∴ MN=2.5CM即圆心M到直线OA的距离d=2.5cm(2)当r=2cm时,
∵d> r,
∴⊙M与直线OA相离。 (3)当r=4cm时,
∵d< r,
∴⊙M与直线OA相交。(1)当r=2.5cm时,
∵d = r,
∴⊙M与直线OA相切。 判定直线 与圆的位置关系的方法有____种:(1)根据定义,由__________________
的个数来判断;(2)根据性质,由____________________
的关系来判断。在实际应用中,常采用第二种方法判定。两直线 与圆的公共点圆心到直线的距离d与半径r小结:0d>r1d=r切点切线2d
1.⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l
与⊙O没有公共点,则d为( ):
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线
和⊙O的位置关系是( ):
A.相离 B.相交 C.相切 D.相切或相交
3.判断:若直线和圆相切,则该直线和圆一定有一个公共点.( )
4.等边三角形ABC的边长为2,则以A为圆心,半径为1.73的圆
与直线BC的位置关系是 ,以A为圆心,
为半径的圆与直线BC相切.AC√相离
