人教版五年级上学期数学第一单元1.3积的近似数(课件)(共18张PPT)
文档属性
| 名称 | 人教版五年级上学期数学第一单元1.3积的近似数(课件)(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 15:19:28 | ||
图片预览





文档简介
(共18张PPT)
积的近似数
教学目标
1. 掌握求小数乘法的积的近似数的方法,能根据要求与实际需要取积的近似数。
2. 经历求小数乘法的积的近似数的过程,能运用迁移的方法主动学习新知。
3. 在解决实际问题的过程中,进一步体会数学与生活的密切联系,提升思维的灵活性。
教学重点:正确地进行“四舍五入”。
教学难点:应用“四舍五入”法取积的近似数。
人的嗅觉细胞约有0.049亿个,狗的嗅觉细胞个数是人的45倍。狗约有多少亿个嗅觉细胞?(得数保留一位小数。)
互动新授
在实际应用中,小数乘法的积往往不需要保留很多
的小数位数,这时可以根据需要,按“四舍五入”
法保留一定的小数位数,求出积的近似数。
看第二位(百分位)上的数用“四舍五入”法取近似数。
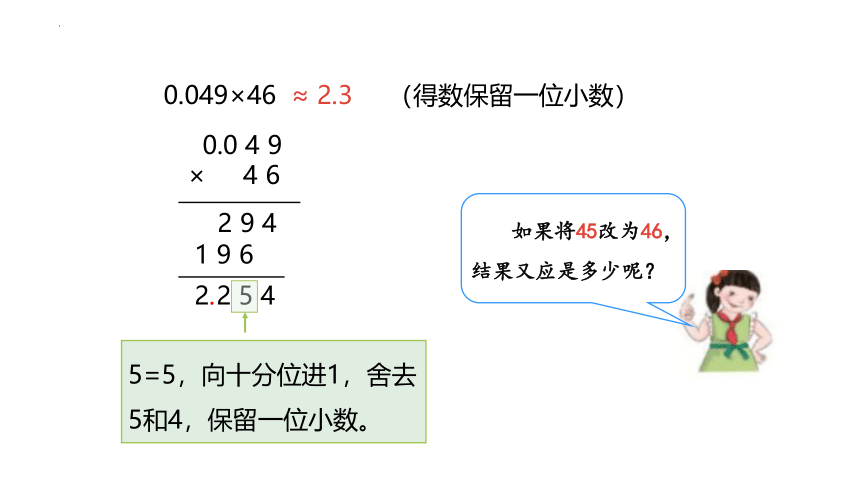
0.049×46
0.0 4 9
× 4 6
2 9 4
1 9 6
2 2 5 4
.
≈ 2.3
(得数保留一位小数)
5=5,向十分位进1,舍去5和4,保留一位小数。
如果将45改为46,结果又应是多少呢?
0.049×45≈ (亿个)
2 4 5
0. 0 4 9
×
4 5
三位小数
1 9 6
2 2 0 5
.
0<5,舍去0和5,保留一位小数。
2.2
总结:求积的近似数,要先算出积,然后看要求保留的小数数位的下一位上的数字,再根据“四舍五入”法求积的近似数,最后用“≈”连接。
0
0.049×45≈2.2
0.0 4 9
× 4 5
2 4 5
1 9 6
2 .2 0 5
(得数保留一位小数。)
百分位
0<5,舍去尾数
0.0 4 9
× 4 5
2 4 5
1 9 6
2 .2 0 5
千分位
5>4,向前一位进1
1
0.049×45≈2.21
(得数保留两位小数。)
求积的近似数时,要先算出相乘的积,然后看要保留的小数的后一位,用“四舍五入”法取近似数。在写横式得数时,注意要用约等号。
0.049×45
人的嗅觉细胞约有0.049亿个,狗的嗅觉细胞个数是人的45倍。狗约有多少亿个嗅觉细胞?(得数保留 小数。)
0.0 4 9
× 4 5
2 4 5
1 9 6
.
≈2.21(亿个)
答:狗约有2.21亿个嗅觉细胞。
保留两位小数,要看千分位上的数。
5=5,舍去5,并向前一位进1
2 2 0 5
1
①先算出积;
②然后看需要保留数位的下一位数字;
③再按照“四舍五入”的方法求出结果,用“≈”表示。
两位
人的嗅觉细胞约有0.049亿个,狗的嗅觉细胞
个数是人的45倍。狗约有多少亿个嗅觉细胞?
(得数保留一位小数。)
“0.049亿”是准确数,还是近似数?
世界上第一台电子计算机很大,它的质量相当于6头5.85吨重的大象,这台计算机有多重?(得数保留整数)一般的 重2.5kg。5.85×6=35.1≈35(吨)答:这台计算机35吨重。
1. 8.697保留一位小数是( ),保留两位小数是( )。
2. 4.5×2.9得数保留一位小数约是( )。
3. 0.32×0.51得数保留两位小数约是( )。
4. 一个两位小数,保留一位小数约是4.7,那么这个两位小数最小是( ),最大是( )。
4.一种大米的价格是每千克3.85元,买2.5kg应
付多少钱?
3.85×2.5 (元)
(教材第11页“做一做”2)
=9.625
≈9.63(元)
答:买2.5kg应付9.63元。
在计算有关钱的问题时,即使没有要求取近似数,如果最后结果的小数位数多于两位,也要根据实际情况保留两位小数。
分
取近似数
1
总价=单价x数量
这个结果正确吗?
?
0.
0.8×0.9≈
2
0.8
× 0.9
7
<5
2
故舍去2
0.7
0.7
得数保留一位小数
1.7×0.45≈
得数保留两位小数
0.765
6
5
1.7
× 0.45
8
8
5
=5
故向百分位进1
0.76
0.77
计算下列各题。
(教科书第11页做一做1)
如何取积的近似数
1、要保留到哪一位,就看它的下一位。
2、如果小于5,就将后面的数舍去。
3、如果大于或等于5就向前一位进1。
≈16.7
≈27.8
≈0.10
≈4.51
两种情况:
一种是“5”,千分位只能大于或等于5才能进一,其中最小的数是5,则这个三位小数最小是2.455。
一种是“6”,千分位上的数要舍去,只能是小于5的数。小于5的数中最大的是4,
所以这个三位小数最大是2.464。
一个三位小数四舍五入到百分位约是2.46,
这个三位小数最大是( ),最小是( )。
进1之后前面满“10”
要“写0进1”
四舍五入进1的时候,如果前面是9+1=10,要继续进1,写0进1。
如果前面还是9+1=10,继续进1。
最后要注意0不能删除。
Goodbye~
感谢聆听,下期再会
积的近似数
教学目标
1. 掌握求小数乘法的积的近似数的方法,能根据要求与实际需要取积的近似数。
2. 经历求小数乘法的积的近似数的过程,能运用迁移的方法主动学习新知。
3. 在解决实际问题的过程中,进一步体会数学与生活的密切联系,提升思维的灵活性。
教学重点:正确地进行“四舍五入”。
教学难点:应用“四舍五入”法取积的近似数。
人的嗅觉细胞约有0.049亿个,狗的嗅觉细胞个数是人的45倍。狗约有多少亿个嗅觉细胞?(得数保留一位小数。)
互动新授
在实际应用中,小数乘法的积往往不需要保留很多
的小数位数,这时可以根据需要,按“四舍五入”
法保留一定的小数位数,求出积的近似数。
看第二位(百分位)上的数用“四舍五入”法取近似数。
0.049×46
0.0 4 9
× 4 6
2 9 4
1 9 6
2 2 5 4
.
≈ 2.3
(得数保留一位小数)
5=5,向十分位进1,舍去5和4,保留一位小数。
如果将45改为46,结果又应是多少呢?
0.049×45≈ (亿个)
2 4 5
0. 0 4 9
×
4 5
三位小数
1 9 6
2 2 0 5
.
0<5,舍去0和5,保留一位小数。
2.2
总结:求积的近似数,要先算出积,然后看要求保留的小数数位的下一位上的数字,再根据“四舍五入”法求积的近似数,最后用“≈”连接。
0
0.049×45≈2.2
0.0 4 9
× 4 5
2 4 5
1 9 6
2 .2 0 5
(得数保留一位小数。)
百分位
0<5,舍去尾数
0.0 4 9
× 4 5
2 4 5
1 9 6
2 .2 0 5
千分位
5>4,向前一位进1
1
0.049×45≈2.21
(得数保留两位小数。)
求积的近似数时,要先算出相乘的积,然后看要保留的小数的后一位,用“四舍五入”法取近似数。在写横式得数时,注意要用约等号。
0.049×45
人的嗅觉细胞约有0.049亿个,狗的嗅觉细胞个数是人的45倍。狗约有多少亿个嗅觉细胞?(得数保留 小数。)
0.0 4 9
× 4 5
2 4 5
1 9 6
.
≈2.21(亿个)
答:狗约有2.21亿个嗅觉细胞。
保留两位小数,要看千分位上的数。
5=5,舍去5,并向前一位进1
2 2 0 5
1
①先算出积;
②然后看需要保留数位的下一位数字;
③再按照“四舍五入”的方法求出结果,用“≈”表示。
两位
人的嗅觉细胞约有0.049亿个,狗的嗅觉细胞
个数是人的45倍。狗约有多少亿个嗅觉细胞?
(得数保留一位小数。)
“0.049亿”是准确数,还是近似数?
世界上第一台电子计算机很大,它的质量相当于6头5.85吨重的大象,这台计算机有多重?(得数保留整数)一般的 重2.5kg。5.85×6=35.1≈35(吨)答:这台计算机35吨重。
1. 8.697保留一位小数是( ),保留两位小数是( )。
2. 4.5×2.9得数保留一位小数约是( )。
3. 0.32×0.51得数保留两位小数约是( )。
4. 一个两位小数,保留一位小数约是4.7,那么这个两位小数最小是( ),最大是( )。
4.一种大米的价格是每千克3.85元,买2.5kg应
付多少钱?
3.85×2.5 (元)
(教材第11页“做一做”2)
=9.625
≈9.63(元)
答:买2.5kg应付9.63元。
在计算有关钱的问题时,即使没有要求取近似数,如果最后结果的小数位数多于两位,也要根据实际情况保留两位小数。
分
取近似数
1
总价=单价x数量
这个结果正确吗?
?
0.
0.8×0.9≈
2
0.8
× 0.9
7
<5
2
故舍去2
0.7
0.7
得数保留一位小数
1.7×0.45≈
得数保留两位小数
0.765
6
5
1.7
× 0.45
8
8
5
=5
故向百分位进1
0.76
0.77
计算下列各题。
(教科书第11页做一做1)
如何取积的近似数
1、要保留到哪一位,就看它的下一位。
2、如果小于5,就将后面的数舍去。
3、如果大于或等于5就向前一位进1。
≈16.7
≈27.8
≈0.10
≈4.51
两种情况:
一种是“5”,千分位只能大于或等于5才能进一,其中最小的数是5,则这个三位小数最小是2.455。
一种是“6”,千分位上的数要舍去,只能是小于5的数。小于5的数中最大的是4,
所以这个三位小数最大是2.464。
一个三位小数四舍五入到百分位约是2.46,
这个三位小数最大是( ),最小是( )。
进1之后前面满“10”
要“写0进1”
四舍五入进1的时候,如果前面是9+1=10,要继续进1,写0进1。
如果前面还是9+1=10,继续进1。
最后要注意0不能删除。
Goodbye~
感谢聆听,下期再会
