2021-2022学年人教版数学八年级下册 19.1.1变量与函数 强化训练(word版含解析)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册 19.1.1变量与函数 强化训练(word版含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 214.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 17:18:22 | ||
图片预览




文档简介
19.1.1变量与函数强化训练
一、单选题
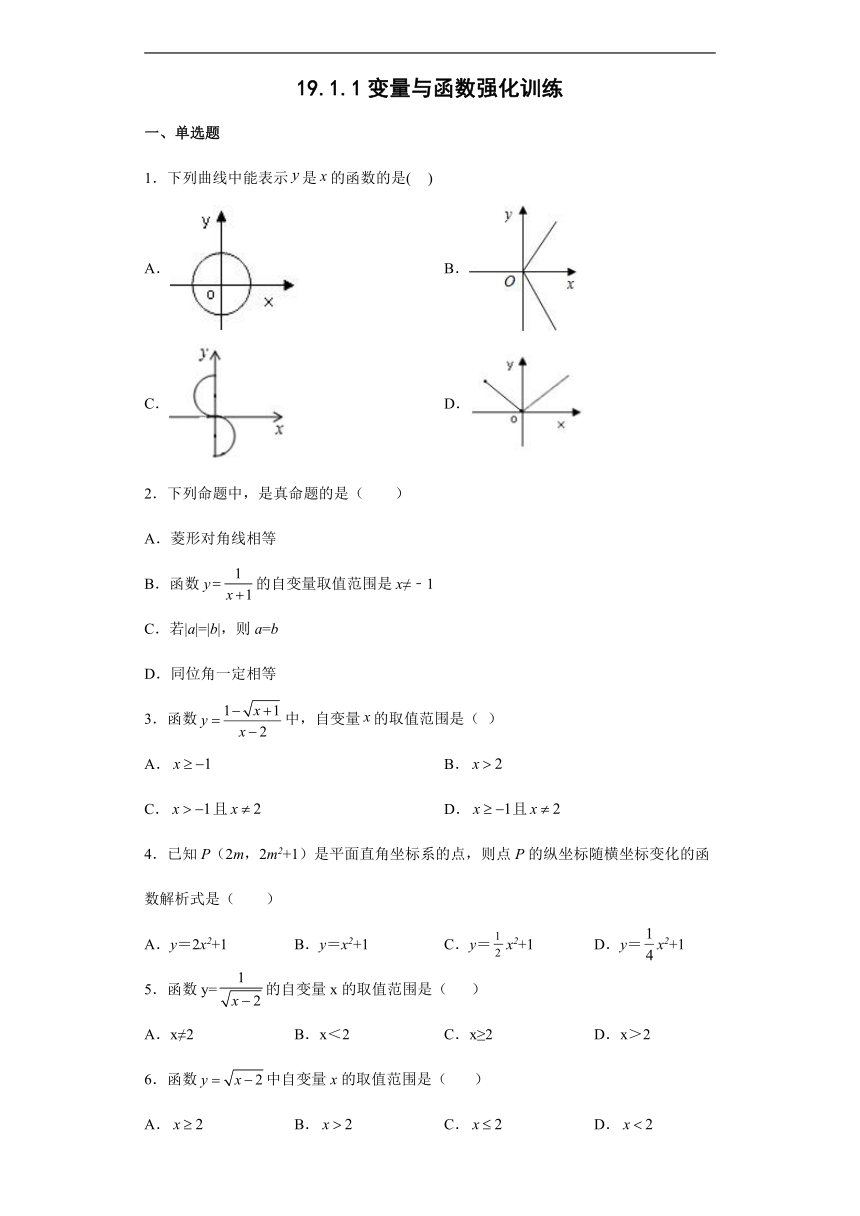
1.下列曲线中能表示是的函数的是( )
A. B.
C. D.
2.下列命题中,是真命题的是( )
A.菱形对角线相等
B.函数y的自变量取值范围是x≠﹣1
C.若|a|=|b|,则a=b
D.同位角一定相等
3.函数中,自变量的取值范围是( )
A. B.
C.且 D.且
4.已知P(2m,2m2+1)是平面直角坐标系的点,则点P的纵坐标随横坐标变化的函数解析式是( )
A.y=2x2+1 B.y=x2+1 C.y=x2+1 D.y=x2+1
5.函数y=的自变量x的取值范围是( )
A.x≠2 B.x<2 C.x≥2 D.x>2
6.函数中自变量x的取值范围是( )
A. B. C. D.
7.下列各式中,y不是x的函数关系的是( )
A.y=x B.y=x2+1 C.y=‖x‖ D.y=±x
8.在圆周长计算公式C=2πr中,对半径不同的圆,变量有( )
A.C,r B.π,r C.π D.C,2π,r
9.若代数式有意义,则实数x的取值范围是
A. B.且 C.且 D.
10.函数 y=1﹣的自变量 x 的取值范围是( )
A.x≤1 B.x≥0 C.x>0 D.x≤0.
11.下列式子中,y不是x的函数的是( )
A. B. C. D.
12.函数中自变量的取值范围是( )
A. B. C.且x≠3 D.
二、解答题
13.“十一”期间,小华约同学一起开车到距家100千米的景点旅游,出发前,汽车油箱内储油35升,当行驶80千米时,发现油箱余油量为25升(假设行驶过程中汽车的耗油量是均匀的).
(1)求该车平均每干米的耗油量,并写出行驶路程x(千米)与剩余油量Q(升)的关系式;
(2)当x=60(千米)时,求剩余油量Q的值;
(3)当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
14.圆柱的底面半径是2cm,当圆柱的高h(cm)由大到小变化时,圆柱的体积V(cm3)随之发生变化.
(1)在这个变化过程中,自变量和因变量各是什么
(2)在这个变化过程中,写出圆柱的体积为V与高h之间的关系式
(3)当h由5cm变化到10cm时,V是怎样变化的
15.将长为的长方形白纸,按图中的方法粘合起来,粘合部分的宽为.
(1)求5张白纸粘合后的长度.
(2)设张白纸粘合后的长度为,写出与之间的关系式.并求当时,的值.
16.如图,在Rt△ABC中,已知∠C=90°,边AC=4cm,BC=5cm,点P为CB边上一点,当动点P沿CB从点C向点B运动时,△APC的面积发生了变化.
(1)在这个变化过程中,自变量和因变量各是什么?
(2)如果设CP长为x cm,△APC的面积为y cm,则y与x的关系可表示为_____;
(3)当点P从点D(D为BC的中点)运动到点B时,则△APC的面积从____cm2变到_____cm2.
17.重庆某客运公司的行李托运收费标准是:行李重量是千克时,收费元,以后每增加千克(不足千克按千克计)需增加费用元.
请用表格表示托运行李的质量与费用之间的关系;
在上述变化过程中,自变量和因变量各是什么?
若某人要托运的行李重量为千克,那么他要付费用多少元?
三、填空题
18.函数中自变量x的取值范围是______.
19.函数中自变量x的取值范围是________.
20.某机器工作时,油箱中的余油量(升)与工作时间(时)的关系式为.当时,________.
21.使函数 有意义的 的取值范围是________.
22.已知等腰三角形的周长为60,底边长为,腰长为,则与之间的关系式及自变量的取值范围为_______.
23.夏天高山上的气温从山脚起每升高l00m降低0.7℃,已知山脚下的气温是23℃,则气温y(℃)与上升的高度x(m)之间的关系式为____;当x=500时,y=__;当y=16时,x=__.
24.函数y=中自变量x的取值范围是 .
25.函数中的取值范围是___________.
试卷第1页,共3页
1.D
【详解】
解:由函数的定义可知,x与y的对应关系应该是一对一的关系或多对一的关系,据此排除A,B,C,
故选D.
2.B
【详解】
A.菱形的对角线垂直但不一定相等,故错误,是假命题;
B.函数y的自变量取值范围是x≠﹣1,正确,是真命题;
C.若|a|=|b|,则a=±b,故错误,是假命题;
D.只要两直线平行同位角才相等,故错误,是假命题.
故选:B.
3.D
【详解】
根据题意得:,解得x≥-1且x≠2,故选D.
4.C
【详解】
是平面直角坐标系的点
将代入y得,
即点P的纵坐标随横坐标变化的函数解析式是
5.D
【详解】
解:∵函数y=有意义,
∴x-20,
即x>2
6.A
【详解】
解:由二次根式有意义的条件可得:
,
解得:,
故选A.
7.D
【详解】
解:A、y=x,y是x的函数关系,故此选项错误;
B、y=x2+1,y是x的函数关系,故此选项错误;
C、y=‖x‖,y是x的函数关系,故此选项错误;
D、y=±x,y不是x的函数关系,故此选项正确;
故选D.
8.A
【详解】
∵在圆的周长公式C=2πr中,C与r是改变的,π是不变的;
∴变量是C,r,常量是2π.
故选A.
9.B
【详解】
∵代数式有意义,∴x﹣1≥0,且x﹣2≠0,
解得:x≥1且x≠2.
故选B.
10.B
【详解】
根据题意得到:x≥0,
故选B.
11.B
【详解】
对于x的每一个取值,y都有唯一确定的值,y是x的函数,
∵选项A、C、D ,当x取值时,y有唯一的值对应;选项B,当x=2时,y=±1,y由两个值,
∴选项B中,y不是x的函数.
12.C
【详解】由题意得:,
解得:x≥2且x≠3,
13.(1)Q=35﹣0.125x;(2)剩余油量Q的值为27.5升;(3)他们能在汽车报警前回到家.
【详解】
解:(1)该汽车平均每千米的耗油量为(35﹣25)÷80=0.125(升/千米),
∴行驶路程x(千米)与剩余油量Q(升)的关系式为Q=35﹣0.125x;
(2)当x=60时,Q=35﹣0.125×60=27.5(升),
答:当x=60(千米)时,剩余油量Q的值为27.5升;
(3)他们能在汽车报警前回到家,
(35﹣3)÷0.125=256(千米),
由256>200知他们能在汽车报警前回到家.
14.(1)自变量是圆柱的高,因变量是圆柱的体积;(2)V=4πh;(3)h越来越大时,V也越来越大,V从20πcm3变化到40πcm3
【详解】
(1)自变量是圆柱的高,因变量是圆柱的体积;
(2)体积V与高h之间的关系式V=4πh;
(3)当h=5cm时,V=20πcm3;
当h=10cm时,V=40πcm3.
当h越来越大时,V也越来越大;V从20πcm3变化到40πcm3
15.(1)5张白纸粘合后的长度是;(2),.
【详解】
解:(1).
答:5张白纸粘合后的长度是.
(2),
当时,.
16.(1) 自变量是CP的长,因变量是△APC的面积;(2) y=2x;(3)5,10
【详解】
(1)自变量是CP的长,因变量是△APC的面积;
(2)y=×4×x=2x
所以y与x的关系可表示为y=2x;
(3)当x=时,y=5;当x=5时,y=10,
所以△APC的面积从5cm2变到10cm2.
17.(1)见解析;(2)自变量是运送行李的质量,因变量是运费;(3)他要付费用19元.
【详解】
(1)由题意可得:
运费/元 4 5 6 7 8 9 …
质量/千克 1 2 3 4 5 6 …
(2)在上述变化过程中,自变量是运送行李的质量,因变量是运费;
(3)由收费标准,得(16-1)+4=19元,
答:他要付费用19元.
18.
【详解】
由题意得,,
解得:-2故答案为-219.x 1
【详解】
根据题意得:
则有 ,
解得:x 1.
故答案为x 1
20.
【详解】
当t=3时,Q=40-6×3=22.
故答案是:22.
21. 且
【详解】
解:由题意,得
解得x>-3且.
故答案为x>-3且.
22.
【详解】
底边y与腰长x之间的函数关系式是y=30-x;
由于2>且>0,
所以.
23. y=23-0.007x 19.5 1000
【详解】
每升高l00m降低0.7℃,则每上升1m,降低0.007℃,
则关系式为:y=23-0.007x;
当x=500时,y=23-0.007×500=19.5;
当y=16时,23-0.007x=16,
解得:x=1000.
24.x≥1且x≠2.
【详解】
解:由题意得,
解得:x≥1且x≠2,
故答案为x≥1且x≠2.
25.
【详解】
试题分析:根据二次根式及分式有意义的条件,列出不等式组即可.
解:由可知,
解得,
故答案为
一、单选题
1.下列曲线中能表示是的函数的是( )
A. B.
C. D.
2.下列命题中,是真命题的是( )
A.菱形对角线相等
B.函数y的自变量取值范围是x≠﹣1
C.若|a|=|b|,则a=b
D.同位角一定相等
3.函数中,自变量的取值范围是( )
A. B.
C.且 D.且
4.已知P(2m,2m2+1)是平面直角坐标系的点,则点P的纵坐标随横坐标变化的函数解析式是( )
A.y=2x2+1 B.y=x2+1 C.y=x2+1 D.y=x2+1
5.函数y=的自变量x的取值范围是( )
A.x≠2 B.x<2 C.x≥2 D.x>2
6.函数中自变量x的取值范围是( )
A. B. C. D.
7.下列各式中,y不是x的函数关系的是( )
A.y=x B.y=x2+1 C.y=‖x‖ D.y=±x
8.在圆周长计算公式C=2πr中,对半径不同的圆,变量有( )
A.C,r B.π,r C.π D.C,2π,r
9.若代数式有意义,则实数x的取值范围是
A. B.且 C.且 D.
10.函数 y=1﹣的自变量 x 的取值范围是( )
A.x≤1 B.x≥0 C.x>0 D.x≤0.
11.下列式子中,y不是x的函数的是( )
A. B. C. D.
12.函数中自变量的取值范围是( )
A. B. C.且x≠3 D.
二、解答题
13.“十一”期间,小华约同学一起开车到距家100千米的景点旅游,出发前,汽车油箱内储油35升,当行驶80千米时,发现油箱余油量为25升(假设行驶过程中汽车的耗油量是均匀的).
(1)求该车平均每干米的耗油量,并写出行驶路程x(千米)与剩余油量Q(升)的关系式;
(2)当x=60(千米)时,求剩余油量Q的值;
(3)当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
14.圆柱的底面半径是2cm,当圆柱的高h(cm)由大到小变化时,圆柱的体积V(cm3)随之发生变化.
(1)在这个变化过程中,自变量和因变量各是什么
(2)在这个变化过程中,写出圆柱的体积为V与高h之间的关系式
(3)当h由5cm变化到10cm时,V是怎样变化的
15.将长为的长方形白纸,按图中的方法粘合起来,粘合部分的宽为.
(1)求5张白纸粘合后的长度.
(2)设张白纸粘合后的长度为,写出与之间的关系式.并求当时,的值.
16.如图,在Rt△ABC中,已知∠C=90°,边AC=4cm,BC=5cm,点P为CB边上一点,当动点P沿CB从点C向点B运动时,△APC的面积发生了变化.
(1)在这个变化过程中,自变量和因变量各是什么?
(2)如果设CP长为x cm,△APC的面积为y cm,则y与x的关系可表示为_____;
(3)当点P从点D(D为BC的中点)运动到点B时,则△APC的面积从____cm2变到_____cm2.
17.重庆某客运公司的行李托运收费标准是:行李重量是千克时,收费元,以后每增加千克(不足千克按千克计)需增加费用元.
请用表格表示托运行李的质量与费用之间的关系;
在上述变化过程中,自变量和因变量各是什么?
若某人要托运的行李重量为千克,那么他要付费用多少元?
三、填空题
18.函数中自变量x的取值范围是______.
19.函数中自变量x的取值范围是________.
20.某机器工作时,油箱中的余油量(升)与工作时间(时)的关系式为.当时,________.
21.使函数 有意义的 的取值范围是________.
22.已知等腰三角形的周长为60,底边长为,腰长为,则与之间的关系式及自变量的取值范围为_______.
23.夏天高山上的气温从山脚起每升高l00m降低0.7℃,已知山脚下的气温是23℃,则气温y(℃)与上升的高度x(m)之间的关系式为____;当x=500时,y=__;当y=16时,x=__.
24.函数y=中自变量x的取值范围是 .
25.函数中的取值范围是___________.
试卷第1页,共3页
1.D
【详解】
解:由函数的定义可知,x与y的对应关系应该是一对一的关系或多对一的关系,据此排除A,B,C,
故选D.
2.B
【详解】
A.菱形的对角线垂直但不一定相等,故错误,是假命题;
B.函数y的自变量取值范围是x≠﹣1,正确,是真命题;
C.若|a|=|b|,则a=±b,故错误,是假命题;
D.只要两直线平行同位角才相等,故错误,是假命题.
故选:B.
3.D
【详解】
根据题意得:,解得x≥-1且x≠2,故选D.
4.C
【详解】
是平面直角坐标系的点
将代入y得,
即点P的纵坐标随横坐标变化的函数解析式是
5.D
【详解】
解:∵函数y=有意义,
∴x-20,
即x>2
6.A
【详解】
解:由二次根式有意义的条件可得:
,
解得:,
故选A.
7.D
【详解】
解:A、y=x,y是x的函数关系,故此选项错误;
B、y=x2+1,y是x的函数关系,故此选项错误;
C、y=‖x‖,y是x的函数关系,故此选项错误;
D、y=±x,y不是x的函数关系,故此选项正确;
故选D.
8.A
【详解】
∵在圆的周长公式C=2πr中,C与r是改变的,π是不变的;
∴变量是C,r,常量是2π.
故选A.
9.B
【详解】
∵代数式有意义,∴x﹣1≥0,且x﹣2≠0,
解得:x≥1且x≠2.
故选B.
10.B
【详解】
根据题意得到:x≥0,
故选B.
11.B
【详解】
对于x的每一个取值,y都有唯一确定的值,y是x的函数,
∵选项A、C、D ,当x取值时,y有唯一的值对应;选项B,当x=2时,y=±1,y由两个值,
∴选项B中,y不是x的函数.
12.C
【详解】由题意得:,
解得:x≥2且x≠3,
13.(1)Q=35﹣0.125x;(2)剩余油量Q的值为27.5升;(3)他们能在汽车报警前回到家.
【详解】
解:(1)该汽车平均每千米的耗油量为(35﹣25)÷80=0.125(升/千米),
∴行驶路程x(千米)与剩余油量Q(升)的关系式为Q=35﹣0.125x;
(2)当x=60时,Q=35﹣0.125×60=27.5(升),
答:当x=60(千米)时,剩余油量Q的值为27.5升;
(3)他们能在汽车报警前回到家,
(35﹣3)÷0.125=256(千米),
由256>200知他们能在汽车报警前回到家.
14.(1)自变量是圆柱的高,因变量是圆柱的体积;(2)V=4πh;(3)h越来越大时,V也越来越大,V从20πcm3变化到40πcm3
【详解】
(1)自变量是圆柱的高,因变量是圆柱的体积;
(2)体积V与高h之间的关系式V=4πh;
(3)当h=5cm时,V=20πcm3;
当h=10cm时,V=40πcm3.
当h越来越大时,V也越来越大;V从20πcm3变化到40πcm3
15.(1)5张白纸粘合后的长度是;(2),.
【详解】
解:(1).
答:5张白纸粘合后的长度是.
(2),
当时,.
16.(1) 自变量是CP的长,因变量是△APC的面积;(2) y=2x;(3)5,10
【详解】
(1)自变量是CP的长,因变量是△APC的面积;
(2)y=×4×x=2x
所以y与x的关系可表示为y=2x;
(3)当x=时,y=5;当x=5时,y=10,
所以△APC的面积从5cm2变到10cm2.
17.(1)见解析;(2)自变量是运送行李的质量,因变量是运费;(3)他要付费用19元.
【详解】
(1)由题意可得:
运费/元 4 5 6 7 8 9 …
质量/千克 1 2 3 4 5 6 …
(2)在上述变化过程中,自变量是运送行李的质量,因变量是运费;
(3)由收费标准,得(16-1)+4=19元,
答:他要付费用19元.
18.
【详解】
由题意得,,
解得:-2
【详解】
根据题意得:
则有 ,
解得:x 1.
故答案为x 1
20.
【详解】
当t=3时,Q=40-6×3=22.
故答案是:22.
21. 且
【详解】
解:由题意,得
解得x>-3且.
故答案为x>-3且.
22.
【详解】
底边y与腰长x之间的函数关系式是y=30-x;
由于2>且>0,
所以.
23. y=23-0.007x 19.5 1000
【详解】
每升高l00m降低0.7℃,则每上升1m,降低0.007℃,
则关系式为:y=23-0.007x;
当x=500时,y=23-0.007×500=19.5;
当y=16时,23-0.007x=16,
解得:x=1000.
24.x≥1且x≠2.
【详解】
解:由题意得,
解得:x≥1且x≠2,
故答案为x≥1且x≠2.
25.
【详解】
试题分析:根据二次根式及分式有意义的条件,列出不等式组即可.
解:由可知,
解得,
故答案为
