人教版数学七年级下册 8.2 消元--解二元一次方程组 课件(共16张PPT)
文档属性
| 名称 | 人教版数学七年级下册 8.2 消元--解二元一次方程组 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 312.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 10:29:54 | ||
图片预览






文档简介
(共16张PPT)
消元--解二元一次方程组
学习目标
1. 巩固用代入消元法解二元一次方程组.
2. 会用二元一次方程组解决简单实际问题.
新知讲解
2x +(12-x)=20
你能设一个未知数(比如设胜x场,) ,根据题意列出一元一次方程吗?
胜 负 合计
场数
积分
(12-x)
12
(12-x)
x
20
2x
你能设两个未知数(比如设胜x场,负y场) ,根据题意列出方程吗?
思考
胜 负 合计
场数
积分
y
12
y
x
20
2x
用方程表示为:
2.能体会“代入法”解二元一次方程组的基本思路,体会化归思想。
1.会用代入消元法解一些简单的二元一次方程组。
基本思路:
二元一次方程
一般步骤:
⑴变形(选择其中一个方程,把它变形为用含有一个未知数的代数式表示另一个未知数的形式);
⑵代入求解(把变形后的方程代入到另一个方程中,消元后求出未知数的值);
⑶回代求解(把求得的未知数的值代入到变形的方程中,求出另一个未知数的值);
⑷写解(用 的形式写出方程组的解).
消元
一元一次方程
你从上面的学习中,体会到解方程组的基本思路是什么?主要步骤有哪些?
篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分. 某队为了争取较好名次,想在全部22场比赛中得到40分,那么这个队胜负场 数应分别是多少?
探究新知
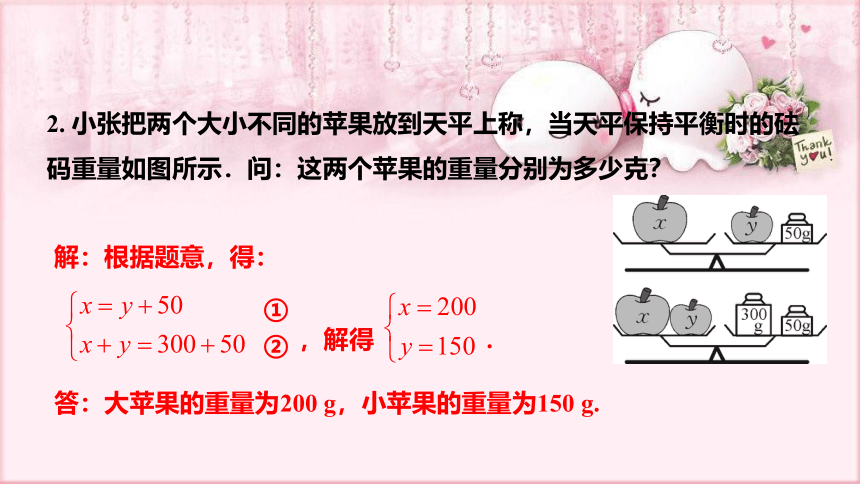
2. 小张把两个大小不同的苹果放到天平上称,当天平保持平衡时的砝码重量如图所示.问:这两个苹果的重量分别为多少克?
解:根据题意,得:
,解得 .
答:大苹果的重量为200 g,小苹果的重量为150 g.
②
①
例1 用代入法解方程组
x-y=3 ①
3x-8y=14 ②
解:由①得: x=y+3 ③
把③代入②得
3(y+3)-8y=14
解这个方程得:y=-1
把y=-1代入③得:x=2
所以这个方程组的解为:
y=-1
x=2
例2 解方程组
3x – 2y = 19
2x + y = 1
解:
①
②
3x – 2y = 19
2x + y = 1
由②得:
y = 1 – 2x
③
把③代入①得:
3x – 2(1 – 2x)= 19
3x – 2 + 4x = 19
3x + 4x = 19 + 2
7x = 21
x = 3
把x = 3代入③,得
y = 1 – 2x
= 1 - 2×3
= - 5
∴
x = 3
y = - 5
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数(变形)
2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值(代入求解)
3、把这个未知数的值再代入一次式,求得另一个未知数的值(再代求解)
4、写出方程组的解(写解)
用代入法解二元一次方程组的一般步骤
1.用代入消元法解下列方程组
⑴
y=2x
2x+5y=12
(2)
x+y=7
4x-y=3
解:
①
②
把①代入②得
解这个方程得:x=1
把x=1代入①得:y=-1
∴方程组的解是
解:
①
②
由②得: y=4x-3 ③
把③代入①得
x+4x-3=7
解这个方程得:x=2
把x=2代入③得:y=5
所以这个方程组的解为:
当堂检测
解:设A种产品x吨,B种产品y吨.
2.5x+2y=1200
900x+1000y=530000
类型 所需原料 生产费用
A种产品 2.5 900
B种产品 2 1000
分析:
x吨
y吨
2y
1000y
900x
2.5x
1200
53万
某工厂现有库存某种原料1200吨,可以用来生产A,B两种产品,每生产一吨A种产品需这种原料2.5吨,生产费用900元,每生产一吨B种产品需原料2吨,生产费用1000元,可用来生产这两种产品的资金为53万,问A,B两种产品各生产多少吨,才能使库存原料和资金恰好用完?
能力提升
①
②
分析: ①+②
①左边 + ② 左边 = ① 右边 + ②右边
321 x + 123 y +345x -123y= 666
666x=666
123y和-123y互为相反数……
(321 x + 123 y) + (345 x – 123 y) = 567 + 99
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数(变形)
2、用这个一次式代替另一个方程中的相应未知数,得到一个一元一次方程,求得一个未知数的值(代入)
3、把这个未知数的值代入一次式,求得另一个未知数的值(再代)
4、写出方程组的解(写解)
用代入法解二元一次方程组的一般步骤
解二元一次方程组
用代入法
③回代求解(把求得的未知数的值代入到变形的方程中,求出另一个未知数的值);
④写解(用的形式写出方程组的解)。
总结归纳
代入法解二元一次方程组的一般步骤:
①变形(选择其中一个方程,把它变形为用含有一个未知数的代数式表示另一个代数式);
②代入求解(把变形后的方程代入到另一个方程中,消元后求出未知数的值);
P93:练习:第3、4题.
布置作业
Goodbye~
感谢聆听,下期再会
消元--解二元一次方程组
学习目标
1. 巩固用代入消元法解二元一次方程组.
2. 会用二元一次方程组解决简单实际问题.
新知讲解
2x +(12-x)=20
你能设一个未知数(比如设胜x场,) ,根据题意列出一元一次方程吗?
胜 负 合计
场数
积分
(12-x)
12
(12-x)
x
20
2x
你能设两个未知数(比如设胜x场,负y场) ,根据题意列出方程吗?
思考
胜 负 合计
场数
积分
y
12
y
x
20
2x
用方程表示为:
2.能体会“代入法”解二元一次方程组的基本思路,体会化归思想。
1.会用代入消元法解一些简单的二元一次方程组。
基本思路:
二元一次方程
一般步骤:
⑴变形(选择其中一个方程,把它变形为用含有一个未知数的代数式表示另一个未知数的形式);
⑵代入求解(把变形后的方程代入到另一个方程中,消元后求出未知数的值);
⑶回代求解(把求得的未知数的值代入到变形的方程中,求出另一个未知数的值);
⑷写解(用 的形式写出方程组的解).
消元
一元一次方程
你从上面的学习中,体会到解方程组的基本思路是什么?主要步骤有哪些?
篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分. 某队为了争取较好名次,想在全部22场比赛中得到40分,那么这个队胜负场 数应分别是多少?
探究新知
2. 小张把两个大小不同的苹果放到天平上称,当天平保持平衡时的砝码重量如图所示.问:这两个苹果的重量分别为多少克?
解:根据题意,得:
,解得 .
答:大苹果的重量为200 g,小苹果的重量为150 g.
②
①
例1 用代入法解方程组
x-y=3 ①
3x-8y=14 ②
解:由①得: x=y+3 ③
把③代入②得
3(y+3)-8y=14
解这个方程得:y=-1
把y=-1代入③得:x=2
所以这个方程组的解为:
y=-1
x=2
例2 解方程组
3x – 2y = 19
2x + y = 1
解:
①
②
3x – 2y = 19
2x + y = 1
由②得:
y = 1 – 2x
③
把③代入①得:
3x – 2(1 – 2x)= 19
3x – 2 + 4x = 19
3x + 4x = 19 + 2
7x = 21
x = 3
把x = 3代入③,得
y = 1 – 2x
= 1 - 2×3
= - 5
∴
x = 3
y = - 5
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数(变形)
2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值(代入求解)
3、把这个未知数的值再代入一次式,求得另一个未知数的值(再代求解)
4、写出方程组的解(写解)
用代入法解二元一次方程组的一般步骤
1.用代入消元法解下列方程组
⑴
y=2x
2x+5y=12
(2)
x+y=7
4x-y=3
解:
①
②
把①代入②得
解这个方程得:x=1
把x=1代入①得:y=-1
∴方程组的解是
解:
①
②
由②得: y=4x-3 ③
把③代入①得
x+4x-3=7
解这个方程得:x=2
把x=2代入③得:y=5
所以这个方程组的解为:
当堂检测
解:设A种产品x吨,B种产品y吨.
2.5x+2y=1200
900x+1000y=530000
类型 所需原料 生产费用
A种产品 2.5 900
B种产品 2 1000
分析:
x吨
y吨
2y
1000y
900x
2.5x
1200
53万
某工厂现有库存某种原料1200吨,可以用来生产A,B两种产品,每生产一吨A种产品需这种原料2.5吨,生产费用900元,每生产一吨B种产品需原料2吨,生产费用1000元,可用来生产这两种产品的资金为53万,问A,B两种产品各生产多少吨,才能使库存原料和资金恰好用完?
能力提升
①
②
分析: ①+②
①左边 + ② 左边 = ① 右边 + ②右边
321 x + 123 y +345x -123y= 666
666x=666
123y和-123y互为相反数……
(321 x + 123 y) + (345 x – 123 y) = 567 + 99
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数(变形)
2、用这个一次式代替另一个方程中的相应未知数,得到一个一元一次方程,求得一个未知数的值(代入)
3、把这个未知数的值代入一次式,求得另一个未知数的值(再代)
4、写出方程组的解(写解)
用代入法解二元一次方程组的一般步骤
解二元一次方程组
用代入法
③回代求解(把求得的未知数的值代入到变形的方程中,求出另一个未知数的值);
④写解(用的形式写出方程组的解)。
总结归纳
代入法解二元一次方程组的一般步骤:
①变形(选择其中一个方程,把它变形为用含有一个未知数的代数式表示另一个代数式);
②代入求解(把变形后的方程代入到另一个方程中,消元后求出未知数的值);
P93:练习:第3、4题.
布置作业
Goodbye~
感谢聆听,下期再会
